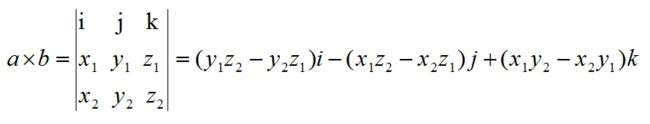数学建模基础(Ⅰ)
MATLAB(矩阵实验室)是MATrix LABoratory的缩写,是一款由美国The
MathWorks公司出品的商业数学软件。MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。除了矩阵运算、绘制函数/数据图像等常用功能外,MATLAB还可以用来创建用户界面及与调用其它语言(包括C、C++、Java、Python和FORTRAN)编写的程序。
尽管MATLAB主要用于数值运算,但利用为数众多的附加工具箱(Toolbox)它也适合不同领域的应用,例如控制系统设计与分析、图像处理、信号处理与通讯、金融建模和分析等。另外还有一个配套软件包Simulink,提供一个可视化开发环境,常用于系统模拟、动态/嵌入式系统开发等方面。
From Wikipedia
另外,Matlab在上世纪七十年代前由Fortran编写,后来用C改写。
根据所用参考书将学习分为三部分,数值计算、符号计算、图形可视化。
向量与矩阵运算
符号计算
MATLAB绘图
向量与矩阵运算
MATLAB的是主要数据对象是矩阵,标量、行向量、列向量都是它的特例,最基本的功能是矩阵运算。
一、向量及其运算
向量生成有直接输入向量、冒号生成向量、线性等分生成向量等方法。
直接输入向量,使用逗号或空格分割元素生成行向量,使用分号或回车分割向量元素生成列向量,这里注意行向量维度需要一致,列向量维度需要一致,否则报错。
>> [1,2,3;4 5 6;7,8 9]
ans =
1 2 3
4 5 6
7 8 9
冒号生成向量,格式为x1:x2:x3,x1为初始值,x2为步长、x3为终止值,x2缺省为1。
>> [3:-1:1;6:-2:2;9:-3:3]
ans =
3 2 1
6 4 2
9 6 3
线性等分生成向量,使用线性等分函数linspace,格式为y=linspace(x1,x2,n),x1表示起始值,x2表示终止值,n表示产生n维向量。与上方法相同,生成的向量都是行向量,如需列向量使用’转置即可。
>> [linspace(1,3,3)' linspace(1,3,3)' linspace(1,3,3)']
ans =
1 1 1
2 2 2
3 3 3
向量运算这里介绍向量的代数运算、群运算、点积叉积混合积等运算。
向量的代数运算包括和差、数乘、平移,设x=[x1 x2 x3],y=[y1 y2 y3],a,b。
和差x±y=[x1±y1 x2±y2 x3±y3],数乘a*x=[a*x1 a*x2 a*x3],平移x+b=[x1+b x2+b x3+b]。
>> x=[1 3 5];y=[2 4 6];
>> x+y,x-y,2*x,x+3
ans =
3 7 11
ans =
-1 -1 -1
ans =
2 6 10
ans =
4 6 8
群运算,包括向量间的乘法、除法、乘幂等运算。设x=[x1 x2 x3],y=[y1 y2 y3]。
元素群乘法x.*y=[x1*y1 x2*y2 x3*y3],元素群右除x./y=[x1/y1 x2/y2 x3/y3],元素群左除x.\y=[y1/x1 y2/x2 y3/x3],
元素群乘幂x.^5=[x1^5 x2^5 x3^5],元素群乘幂7.^x=[7^x1 7^x2 7^x3],元素群乘幂x.^y=[x1^y1 x2^y2 x3^y3]。
>> x=[1 2 3];y=[4 5 6];
>> x.*y,x./y,x.\y,x.^5,7.^x,x.^y
ans =
4 10 18
ans =
0.2500 0.4000 0.5000
ans =
4.0000 2.5000 2.0000
ans =
1 32 243
ans =
7 49 343
ans =
1 32 729
点积叉积混合积运算,点积(内积)MATLAB中有函数dot(a,b),叉积(外积)MATLAB中则有函数cross(a,b),混合积即可由两个函数共同实现,这里对点乘和叉乘运算进行简要解释扩展。
向量的点乘,也叫向量的数量积、内积、点积、无向积等,对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。
数量积的几何意义是表示在b向量在a向量方向上的投影与a模长的乘积,也可以用来计算两向量夹角等。a·b = |a|*|b|*cosθ。
向量的叉乘,又叫向量的向量积、外积、叉积、有向积等,叉乘的运算结果是一个向量。并且两个向量的向量积与这两个向量组成的坐标平面垂直。
在三维几何中,向量a和向量b的向量积结果是法向量,则可以通过两个向量的向量积,生成第三维,从而构建XYZ坐标系。在二维空间中,向量积的几何意义是:axb等于由向量a和向量b构成的平行四边形的面积。a∧b = |a|*|b|*sinθ。
From -牧野-
原文中不准确和冗余之处已纠正。
向量的内外积是线性代数的内容,不过已经全部忘光了,身为计算机科学系的学生十分惭愧,这里再做一点补充。
数量积在物理中可以通过W=F·s=|F||s|cosθ理解,力对物体做的功=力在运动方向上的分量对物体做的功。
向量积在物理中可以通过M=r×F=|r||F|sinθ理解,也就是一个力对一个定点的矩,当F与向径r不垂直时,二者有个夹角θ。
另外a∧b的方向:与这两个向量所在平面垂直,且遵守右手定则。(若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。c=a∧b)
下面是计算演示。
>> x=[1 2 3];y=[3 4 5];
>> dot(x,y), cross(x,y), dot(x,cross(y,cross(x,y)))
ans =
26
ans =
-2 4 -2
ans =
24
二、矩阵及其运算
矩阵生成有直接输入矩阵、M文件输入矩阵、函数生成矩阵等方法。
直接输入矩阵,规模小时非常实用,矩阵用[]标识,行内用逗号或空格分割元素,行与行之间用分号或回车分割,矩阵元素也可以写为运算表达式。
>> [1,2,3;exp(1),7/6,abs(-2.8)]
ans =
1.0000 2.0000 3.0000
2.7183 1.1667 2.8000
M文件输入矩阵,M文件是一种可以在MATLAB系统中运行的文本文件,它可以分为命令式文件和函数式文件,主要使用命令式的M文件创建矩阵。
这里对M文件也进行补充扩展。
MATLAB涉及的文件类型有.m .mat .asv .fig .xml .sxl等许多种,MATLAB提供了程序设计功能,即对应以.m为扩展名的文件,简称M文件。M文件有两种形式:命令式文件(Script)和函数式文件(Function)。
命令式文件就是命令行的简单叠加,这样就解决了用户在命令窗中输入许多命令的麻烦,也避免了重复性工作。无输入参数和返回,生成的变量均为全局变量,通过clear等命令可以清除。
函数式文件主要解决参数传递和函数调用问题,首行必须用function标识,可以有输入参数和返回值,过程中生成的变量会在调用结束后被销毁。
Basis_3.m
aa=[1,2,3;4,5,6;7,8,9]
>> Basis_3
aa =
1 2 3
4 5 6
7 8 9
函数生成矩阵,有ones(全1阵)、zeros(全0阵)、eye(单位阵)、rand(均匀分布随机阵)等特殊矩阵。直接演示。
Basis_4.m
a=[1,2,3;4,5,6;7,8,9];
b=ones(2,3);
c=ones(size(a));
d=zeros(3,2);
e=eye(3);
f=rand(3,3);
>> Basis_4
>> a,b,c,d,e,f,g
a =
1 2 3
4 5 6
7 8 9
b =
1 1 1
1 1 1
c =
1 1 1
1 1 1
1 1 1
d =
0 0
0 0
0 0
e =
1 0 0
0 1 0
0 0 1
f =
0.9649 0.9572 0.1419
0.1576 0.4854 0.4218
0.9706 0.8003 0.9157
g =
0.8147 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
矩阵运算这里介绍四则运算、分块矩阵、矩阵函数运算、矩阵特殊操作等运算形式。
四则运算,加减法时需同阶;乘法时左矩阵的列数应该等于右矩阵的行数;除法分左除\和右除/两种,左除时AX=B解为X=A\B,右除时XA=B解为X=A/B。
在传统MATLAB算法中,右除需要先计算矩阵的逆再做矩阵的乘法,而左除则不需要计算矩阵的逆,直接进行除法运算,实际计算中也应用较多。
下文演示中可以看出元素群运算和四则运算的区别,方便起见用方阵运算,以及通过矩阵除法的应用之一「解方程组」来学习左右除。
Basis_5.m
a=[1,2,3;4,5,6;7,8,9];
b=[2,1,3;2,-3,-3;-2,3,3];
>> Basis_5
>> a+b,a*b,a.*b
ans =
3 3 6
6 2 3
5 11 12
ans =
0 4 6
6 7 15
12 10 24
ans =
2 2 9
8 -15 -18
-14 24 27
{ x + y + z = 8 2 x + 3 y − z = 7 5 x − 2 y + z = 3 x = 1 y = 3 z = 4 \begin{cases} x+y+z=8\\ 2x+3y-z=7\\ 5x-2y+z=3 \end{cases}\\ \ \\ x=1\ \ \ y=3\ \ \ z=4 ⎩⎪⎨⎪⎧x+y+z=82x+3y−z=75x−2y+z=3 x=1 y=3 z=4
Basis_5.m
c=[1,1,1;2,3,-1;5,-2,1];
d=[8;7;3];
>> Basis_5
>> c\d
ans =
1.0000
3.0000
4.0000
分块矩阵,当需要对矩阵的某部分操作时即可用A(vr,vc)产生矩阵块,也可以拼接产生新矩阵。
Basis_5.m
e=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15];
vr=[1:3];vc=[2:3];
f1=ones(2,3);%二行三列,2x3全一阵
f2=zeros(2,2);%二阶方阵,2x2全零阵
f3=eye(3);%三阶方阵,3x3单位矩阵
f4=6*ones(3,2);%三行二列,3x2全六阵
F=[f1,f2;f3,f4];
>> Basis_5
>> e(vr,vc),F
ans =
2 3
7 8
12 13
F =
1 1 1 0 0
1 1 1 0 0
1 0 0 6 6
0 1 0 6 6
0 0 1 6 6
矩阵函数运算,比如矩阵A的逆inv(A),或者方阵A的行列式det(A),还有矩阵A的秩rank(A),众多函数在以后用到时详细学习。这里用上文的c=[1,1,1;2,3,-1;5,-2,1]演示。
>> inv(c),det(c),rank(c)
ans =
-0.0400 0.1200 0.1600
0.2800 0.1600 -0.1200
0.7600 -0.2800 -0.0400
ans =
-25
ans =
3
矩阵特殊操作,例如矩阵变维、变向、抽取等,下文将演示矩阵变维的操作。reshape(A,Row,Column),A为变维的原矩阵,Row为变维后行数,Column为变维后列数,结果为变维后矩阵。
>> a=1:24,b=reshape(a,4,6)
b =
1 5 9 13 17 21
2 6 10 14 18 22
3 7 11 15 19 23
4 8 12 16 20 24
符号计算
一、符号变量与符号表达式
在数值计算中,变量都是数值变量。在符号运算中,变量都是以字符形式保存运算。符号可由sym或syms创建,sym只能一次创建一个符号,syms可创建多个。符号表达式可由符号’'或sym函数创建。
findsym(f,n)可以查询符号表达式使用到了哪n个符号变量,n缺省时表示查询全部。
有时符号运算的目的是得到精确的数值解,这就需要对解析解进行数值转换,会用到digits、vpa或subs函数,
digits(D)表示函数设置有效数字个数为D的近似解精度,
vpa(S,D)表示符号表达式S在digits(D)精度下的数值解,
subs(S,a,x)表示用x替换符号表达式S中的变量a,产生新的符号表达式,原符号表达式不变。
Basis_6.m
syms a b x y
f='sin(a*x)+cos(b*y)';
g=sym('exp(x)');
s=solve('x^2-3*x+2=0');
h=subs(f,x,pi);
>> Basis_6
>> f,g,h,vpa(s)
f =
sin(a*x)+cos(b*y)
g =
exp(x)
h =
sin(pi*a) + cos(b*y)
ans =
1.0
2.0
二、符号微积分
导数。
diff(S,v,n)表示对表达式S关于变量v求n阶导数,n省略求1阶导,v省略则对默认变量求导。
例如求z=2ysinx^2关于x的一阶、二阶偏导。
Basis_7.m
syms x y n k
s=y*sin(x^2);
diff(s,x,1),diff(s,x,2)
>> Basis_7
ans =
2*x*y*cos(x^2)
ans =
2*y*cos(x^2) - 4*x^2*y*sin(x^2)
当用于算符号矩阵时,是作用于矩阵的每个元素。
Basis_7.m
A=[sin(a*x),cos(a*x);-cos(b*x),-sin(b*x)];
diff(A)
>> Basis_7
ans =
[ a*cos(a*x), -a*sin(a*x)]
[ b*sin(b*x), -b*cos(b*x)]
积分。
int(S,v,a,b)表示对符号表达式关于指定变量v在区间[a,b]内求定积分,若出现无穷区间情形以inf代替。
a,b两变量省略的话,求的就是不定积分。
例如求下面两个积分。
∫ d x x 2 1 + x 2 ∫ − ∞ + ∞ d x 1 + 9 x 2 \int \frac{dx}{x^2 \sqrt{1+x^2}}\ \ \ \ \ \ \ \ \ \int_{-∞}^{+∞} \frac{dx}{1+9x^2} ∫x21+x2dx ∫−∞+∞1+9x2dx
Basis_7.m
s1=1/(x^2*sqrt(1+x^2));
int(s1,x)
s2=1/(1+9*x^2);
int(s2,x,-inf,inf)
>> Basis_7
ans =
-(x^2 + 1)^(1/2)/x
ans =
pi/3
极限。
limit(S,x,a)表示计算符号表达式S在x->a时的极限。
例如求下面问题的左极限。
lim x → 2 x 2 − 4 x − 2 \lim_{x \to 2} \frac{x^2 -4}{x-2} x→2limx−2x2−4
Basis_7.m
f1=(x^2-4)/(x-2);
limit(f1,x,2,'left')
>> Basis_7
ans =
4
级数求和。
symsum(S,v,a,b)表示对符号表达式S关于指定变量v从a到b求和。
例如求下面级数的和。
∑ k = 1 ∞ 1 k 2 \sum\limits_{k=1}^{∞}\frac{1}{k^2} k=1∑∞k21
Basis_7.m
f2=1/k^2;
symsum(f2,k,1,inf)
>> Basis_7
ans =
pi^2/6
幂级数展开。
taylor(S,n)表示对符号函数S关于默认变量的n次麦克劳林展开式。
taylor(S,x,a,‘order’,n)表示对符号函数S关于指定变量x在a点的n次泰勒展开式。
例如将y=cosx在x=pi/3处展开成次数为7的幂级数。
Basis_7.m
taylor(cos(x),x,pi/3,'Order',7)
>> Basis_7
ans =
(3^(1/2)*(x - pi/3)^3)/12 - (3^(1/2)*(x - pi/3))/2 - (3^(1/2)*(x - pi/3)^5)/240 - (x - pi/3)^2/4 + (x - pi/3)^4/48 - (x - pi/3)^6/1440 + 1/2
三、符号简化
因式分解。
factor(S)表示把表达式S分解为多个因式,各因式的系数均为有理数,若S是个整数则对S进行素数分解。
例如。
Basis_8.m
syms x y t
factor(x^8-1)
factor(sym('5230764'))
>> Basis_8
ans =
[ x - 1, x + 1, x^2 + 1, x^4 + 1]
ans =
[ 2, 2, 3, 3, 3, 7, 11, 17, 37]
展开。
expand(S)表示把表达式S分解进行展开。
例如。
Basis_8.m
expand((x-1)^5)
>> Basis_8
ans =
x^5 - 5*x^4 + 10*x^3 - 10*x^2 + 5*x - 1
合并。
collect(S,v)表示对表达式S按照变量v的同幂项进行合并。
例如。
Basis_8.m
f=(x+1)^2*(t+1)^2+3*x^2*t+2*x*t;
collect(f,x)
>> Basis_8
ans =
(3*t + (t + 1)^2)*x^2 + (2*t + 2*(t + 1)^2)*x + (t + 1)^2
简化。
[R,HOW]=simple(S)表示对表达式S尝试不同算法简化,找到表达式的长度最短形式R,HOW为简化过程中的主要方法,不过现在版本已经没有了。
simplify(S)表示对表达式S利用恒等式进行化简。
例如。
Basis_8.m
simplify(sin(x)^2+cos(x)^2)
>> Basis_8
ans =
1
通分。
[N,D]=numden(S)表示将表达式S的各元素转换为分子和分母都是整系数的最佳多项式,N表示分子D表示分母。
例如。
Basis_8.m
[n,d]=numden(x/(2*y)+y/(3*x)+x+y+1)
>> Basis_8
n =
6*x^2*y + 3*x^2 + 6*x*y^2 + 6*x*y + 2*y^2
d =
6*x*y
嵌套。
horner(S)表示将符号多项式S转换成嵌套形式表示,用多层括号表示。
例如。
Basis_8.m
horner(x^4+2*x^3-5*x^2+7*x-8)
>> Basis_8
ans =
x*(x*(x*(x + 2) - 5) + 7) - 8
图形可视化
一、二维图形的绘制
二维曲线图。
MATLAB作图需要先取得图形上一系列的点坐标,即横纵坐标,然后调用plot函数绘制曲线。
plot(x,y,‘s’)中x是横坐标向量,y是纵坐标向量,s为选项字符串,可以控制线型和颜色。
plot(xk,yk,‘s’…)可以绘制多条曲线,但要求各x横坐标向量维数相同,各y纵坐标向量维数相同。
例如绘制弦线。
Basis_9.m
figure(1);
x=0:pi/50:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,'k:',x,y2,'b-');
>> Basis_9
也可以通过hold on/hold off单条绘制得到。
绘制图形时可以用一些命令对图形进行说明,常用的有title,xlabel,ylabel,text,legend,axis,grid,hold等。
Basis_9.m
axis([0,3*pi,-1.5,1.5]);
title('正弦与余弦曲线');
xlabel('x轴');
ylabel('y轴');
legend('sin(x)','cos(x)');
grid('on');
>> Basis_9

子图。
subplot(m,n,p)表示将图形窗口分割为mxn个绘图区,每行n个共m行,区号按行优先编号,且选定第p个区为当前活动区。
这部分不多说,下文中有各种演示。
符号函数画图。
ezplot(‘f’,[xmin,xmax,ymin,ymax])表示绘制函数f在xmin
f1=sinx,x∈[-4pi,4pi];f2=x^2/4-y^2/9=1,x∈[-5,5],y∈[-3,3];f3=exp(x)+sinx,x∈[-1,1]。
Basis_9.m
figure(2);
subplot(1,3,1);
ezplot('sin(x)',[-4*pi,4*pi]);
subplot(1,3,2);
ezplot('x^2/4-y^2/9=1',[-5,5,-3,3]);
subplot(1,3,3);
fplot('exp(x)+sin(x)',[-1,pi]);
>> Basis_9
二、三维图形的绘制
三维曲线图。
最基本的三维曲线绘图函数就是plot3,看函数名就可以看出来是二维函数plot功能的三维扩展,
plot3(x,y,z)表示绘制一条三维曲线,其中x,y,z为三个相同维数的向量,函数绘出这些向量所表示的三维曲线。
plot3(X,Y,Z)绘制多条三维曲线,X,Y,Z是三个相同阶数的矩阵,绘出的是三个矩阵列向量表示的曲线。
plot3(xk,yk,zk,ck…)也可以绘制多条,c表示线型和颜色。
例如绘制三维螺旋线。
x=2cost,y=2sint,z=3t,t∈[0,10pi]。
Basis_9.m
figure(3);
subplot(1,2,1);
t=0:pi/30:10*pi;
x=2*cos(t);
y=2*sin(t);
z=3*t;
plot3(x,y,z);
xlabel('x');
ylabel('y');
zlabel('z');
>> Basis_9
或者ezplot的扩展ezplot3。
Basis_9.m
subplot(1,2,2);
ezplot3('2*cos(t)','2*sin(t)','3*t',[0,10*pi]);
>> Basis_9

三维曲面图。
绘制三维曲面图之前需要对数据处理,得到坐标组,步骤:将自变量x,y离散->使用meshgrid指令生成特定x-y矩阵,
[X,Y]=meshgrid(x,y),X,Y矩阵元素分别表示为所绘曲面在XOY面投影点的x,y轴坐标值,若向量x的维数为m,向量y的维数为n,则X,Y矩阵对应维数为nxm->利用函数z=f(X,Y),计算函数值->利用MATLAB三维曲面绘制函数,绘制三维曲面图。
mesh(X,Y,Z,C)绘制三维曲面网格图,C控制网格颜色。
surf(X,Y,Z,C)绘制三维曲面颜色填充图,C控制网格内区域颜色。
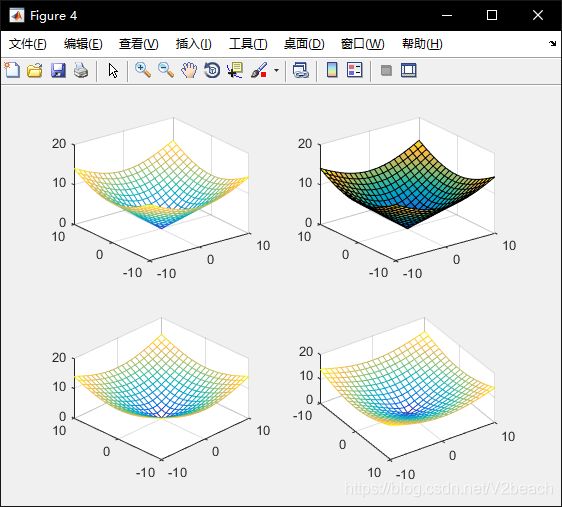
例如绘制z=√(x2+y2),x∈[-10,10],y∈[-10,10]。
Basis_9.m
figure(4);
subplot(2,2,1);
x=-10:1:10;
y=-10:1:10;
[X,Y]=meshgrid(x,y);
Z=sqrt(X.^2+Y.^2);
mesh(X,Y,Z);
subplot(2,2,2);
surf(X,Y,Z);
>> Basis_9
设置观察三维曲面图的视点,使用view(az,el),az是azimuth方位角,el是elevation仰角,以度为单位,默认方位角-37.5°,仰角30°。
az是指,x平行于观察者身体,y垂直于观察者身体,az=0,绕z顺时针运动az为正,逆时针为负。
el是指,当观察者眼睛在xy平面上el=0,向上el为正,向下为负。需要指定点时则view([x,y,z])。
仍以上图为例,以az=-45°,el=45°,和[3,-2,5]处观察。
Basis_9.m
subplot(2,2,3);
mesh(X,Y,Z);
view(-45,45);
subplot(2,2,4);
mesh(X,Y,Z);
view([3,-2,5]);
>> Basis_9
绘制空间曲面符号绘图函数有ezmesh和ezsurf,两函数格式类似,不重复说明。
ezmesh(z(x,y),[xmin,xmax,ymin,ymax])表示在x和y的范围内绘制z。
ez前缀的这几个函数用于处理符号函数,而不加的surf,mesh等用来处理数值函数。
总结
正确的学法不是一边学一边写博客,而是应该将任务划分为几个部分,每部分学完后写博客巩固,将知识扎牢,否则一是拖慢进度,二是学习强度和质量不尽人意。