MATLAB之数学运算

第三部分.数学运算

1.三角函数

函数名称	说明
sin()/sind()	正弦函数，输入值为弧度/角度
cos()/cosd()	余弦函数，输入值为弧度/角度
tan()/tand()	正切函数，输入值为弧度/角度
sec()/secd()	正割函数，输入值为弧度/角度
csc()/cscd()	余割函数，输入值为弧度/角度
cot()/cotd()	余切函数，输入值为弧度/角度
asin()/asind()	反正弦函数，返回值为弧度/角度
acos()/acosd()	反余弦函数，返回值为弧度/角度
acsc()/acscd()	反余割函数，返回值为弧度/角度
asec()/asecd()	反正割函数，返回值为弧度/角度
atan()/atand()	反正切函数，返回值为弧度/角度
acot()/acotd()	反余切函数，返回值为弧度/角度
atan2()	四象限内反正切，返回值为弧度/角度

2.双曲线函数

函数名	说明	函数名	说明
sinh()	双曲正弦	asinh()	反双曲正弦
cosh()	双曲余弦	acos()	反双曲余弦
tanh()	双曲正切	atan()	反双曲正切

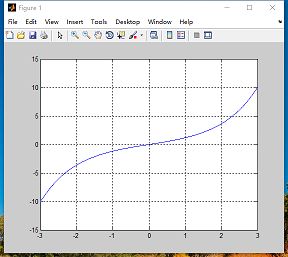
例：

>> x=-3:0.01:3;

>> plot(x,sinh(x))

>> grid on

 

3.复数函数

函数名	说明
abs()	求复数的模
angle()	求复数的相角（弧度制）
real()	求复数的实部
imag()	求复数的虚部
conj()	求复数的共轭值
unwrap()	复数的相角展开
isreal()	判断是否为实数
cplxpair()	按共轭复数对重新排列
complex()	由实部和虚部创建函数

例：

>> a=3+4i

 

a =

 

   3.0000 + 4.0000i

 

>> A=abs(a)

 

A =

 

     5

 

>> al=real(a)

 

al =

 

     3

 

>> a2=imag(a)

 

a2 =

 

     4

 

>> angle_a=angle(a)

 

angle_a =

 

    0.9273

 

>> b=conj(a)

 

b =

 

   3.0000 - 4.0000i

4.求和、乘积和差分

（1）求和函数

一般格式：

sum(x)      %返回数组x的所有值之和，这里x表示一个数组

sum(X)      %返回矩阵X各列元素之和的矩阵

comsum(x)   %返回一个数组x中元素累计和的向量

comsum(X)   %返回矩阵X各列元素之和的矩阵，和sun(X)的结果相同

例.创建一个三维数组B并对其求和及累积和：

>> B(:,:,1)=[1 2 3;2 3 1;3 2 1]

 

B =

 

     1     2     3

     2     3     1

     3     2     1

 

>> B(:,:,2)=[2 4 6;4 6 2;6 4 2]

 

B(:,:,1) =

 

     1     2     3

     2     3     1

     3     2     1

 

 

B(:,:,2) =

 

     2     4     6

     4     6     2

     6     4     2

 

>> Varsum=sum(B)

 

Varsum(:,:,1) =

 

     6     7     5

 

 

Varsum(:,:,2) =

 

    12    14    10

 

>> VarCsum=cumsum(B)

 

VarCsum(:,:,1) =

 

     1     2     3

     3     5     4

     6     7     5

 

 

VarCsum(:,:,2) =

 

     2     4     6

     6    10     8

12    14    10

（2）乘积函数

一般格式：

函数名	说明
prod(x)	返回数组x中各元素乘积，x表示数组
prod(A)	返回按列向量的所有元素的积，然后组成一行向量
prod(A,dim)	给出dim维内的元素乘积
cumprod(x)	返回一个x中各元素累计积的向量，也就是第2个元素是x中前两个元素的累计积
cumprod(A)	返回一个矩阵，其中列元素是A中列元素的累计积
cumprod(A,dim)	给出在dim维内的累计积

例.创建三维数组B并对其求积及累计积：

 

>> B(:,:,1)=[1 2 3;2 3 1;3 2 1]

 

B(:,:,1) =

 

     1     2     3

     2     3     1

     3     2     1

 

 

B(:,:,2) =

 

     2     4     6

     4     6     2

     6     4     2

 

>> B(:,:,2)=[2 4 6;4 6 2;6 4 2]

 

B(:,:,1) =

 

     1     2     3

     2     3     1

     3     2     1

 

 

B(:,:,2) =

 

     2     4     6

     4     6     2

     6     4     2

 

>> Varprod=prod(B)

 

Varprod(:,:,1) =

 

     6    12     3

 

 

Varprod(:,:,2) =

 

    48    96    24

 

>> VarCprod=cumprod(B)

 

VarCprod(:,:,1) =

 

     1     2     3

     2     6     3

     6    12     3

 

 

VarCprod(:,:,2) =

 

     2     4     6

     8    24    12

48    96    24

(3)差分函数

调用格式	说明
diff(x)	给出一个长度为n-1的向量，它的元素是长度为n的向量x中相邻元素的差，如果x=(x1,x2,...,xn),则diff(x)=(x2-x1,x3-x2,...,xn-(xn-1))
diff(A)	在A的第一维内计算相邻元素的差分。对于二维矩阵来说，即diff(A)=A(2:m,:)-A(1:m-1,:)
diff(x,k)	求出第k次差分，diff(x,2)和diff(diff(x))等价
diff(A,k,dim)	在dim维内求出第k次差分

例.已知向量x求其差分：

>> x=[1 3 7 12 35 78]

 

x =

 

     1     3     7    12    35    78

 

>> Vard1=diff(x)

 

Vard1 =

 

     2     4     5    23    43

 

>> Vard2=diff(Vard1)

 

Vard2 =

 

     2     1    18    20

5.最大值和最小值

函数格式	说明
max(x)	返回x中的最大值；如果x为复数，则返回abs(x)的最大值
max(X)	返回一个矩阵，该矩阵的元素包含矩阵X中第一维元素中的最大值。例如，X是一个二维矩阵，则返回的函数为一个向量，它的第一个元素即X中的第一列的最大值，以此类推。若X为复数，则返回abs(X)的最大值
max(A,B)	返回一个与A,B同维数的矩阵，该矩阵的每个元素均为A,B矩阵相同位置元素的最大值
min(x)	返回x中的最小值；如果x为复数，则返回abs(x)的最小值
min(X)	返回一个矩阵，该矩阵的元素包含矩阵X中第一维元素中的最小值。例如，X是一个二维矩阵，则返回的函数为一个向量，它的第一个元素即X中的第一列的最小值，以此类推。若X为复数，则返回abs(X)的最小值
min(A,B)	返回一个与A,B同维数的矩阵，该矩阵的每个元素均为A,B矩阵相同位置的最小值

例.创建三维数组B，并求其最大值：

>> B(:,:,1)=[1 2 3;2 3 1;3 2 1]

 

B(:,:,1) =

 

     1     2     3

     2     3     1

     3     2     1

 

 

B(:,:,2) =

 

     2     4     6

     4     6     2

     6     4     2

 

>> B(:,:,2)=[2 4 6;4 6 2;6 4 2]

 

B(:,:,1) =

 

     1     2     3

     2     3     1

     3     2     1

 

 

B(:,:,2) =

 

     2     4     6

     4     6     2

     6     4     2

 

>> max(B)

 

ans(:,:,1) =

 

     3     3     3

 

 

ans(:,:,2) =

 

     6     6     6

 

>> whos

  Name          Size             Bytes  Class     Attributes

 

  A             1x1                  8  double              

  B             3x3x2              144  double              

  VarCprod      3x3x2              144  double              

  VarCsum       3x3x2              144  double              

  Vard1         1x5                 40  double              

  Vard2         1x4                 32  double              

  Varprod       1x3x2               48  double              

  Varsum        1x3x2               48  double              

  a             1x1                 16  double    complex   

  a2            1x1                  8  double              

  al            1x1                  8  double              

  angle_a       1x1                  8  double              

  ans           1x3x2               48  double              

  b             1x1                 16  double    complex   

  x             1x6                 48  double    

6.简单统计命令

函数	说明
mean(x)	求出向量x的算术平均值
mean(A,dim)	给出一个1xnx...xp的矩阵，它包含A中第1维的各个平均值。如果给出了dim，就在dim维内计算
median(x)	求出向量x中元素的中值
median(A,dim)	给出一个1xnx...xp的矩阵，它包含A中第1维各列的中值。如果给出了dim,就在dim维内计算
std(x)	求出向量x中元素的标准差
std(A,dim)	给出一个1xnx...xp的矩阵，它包含A中第1维各列的标准差。如果给出了dim,就在dim维内计算标准差

例.求算术平均值和中值：

>> A=[1.4 9.3 3.5;1.8 9.8 3.2;1.6 10.2 3.9];

>> mean(A)

 

ans =

 

    1.6000    9.7667    3.5333

 

>> mean(A,2)

 

ans =

 

    4.7333

    4.9333

    5.2333

 

>> Varmed=median(A)

 

Varmed =

 

    1.6000    9.8000    3.5000

 

>> Varstd=std(A)

 

Varstd =

 

    0.2000    0.4509    0.3512

7.排序

函数	说明
sort(x)	返回一个向量x的元素按递增排序的向量。如果元素是复数，则使用绝对值进行排序，即sort(abs(x))
[y,ind]=sort(x)	返回下标向量ind，即y=x(ind).另外，向量y是x中元素按递增排序得到的
sort(A,dim)	对A中各列按递增排序，注意矩阵的行已被改变。如果给出了dim，则在dim维内进行排序
[B,Ind]=sort(A)	返回矩阵Ind和矩阵B，矩阵B的列为矩阵A中按递增排序的列，矩阵Ind的每列对应于上面提到的向量中列ind
sortrows(X,col)	对矩阵A的各行按递增排序。如果行的元素是复数，它们以abs（x）为主，以angle（x）为辅进行排序，如果给出col，则根据指定的列数对行进行排序

例.对给定矩阵升序降序排序：

>> B=[0 5 5;3 0 3;5 3 0]

 

B =

 

     0     5     5

     3     0     3

     5     3     0

 

>> [Ascend,Ind]=sort(B)

 

Ascend =

 

     0     0     0

     3     3     3

     5     5     5

 

 

Ind =

 

     1     2     3

     2     3     2

     3     1     1

 

>> Var_Descend=flipud(sort(B))      

%把矩阵sort(B)上下翻转，并把翻转后的新矩阵返回Var_Descend

 

Var_Descend =

 

     5     5     5

     3     3     3

     0     0     0

8.关系和逻辑运算及多项式运算

（1）关系操作符

关系操作符	功能说明	关系操作符	功能说明
<	小于	>=	大于或者等于
<=	小于等于	==	等于
>	大于	~=	不等于

例：

>> a=magic(3)        %输入一个魔方阵列

 

a =

 

     8     1     6

     3     5     7

     4     9     2

 

>> a>4*ones(3)     %将a与全为4的数组比较

 

ans =

 

     1     0     1

     0     1     1

     0     1     0

（2）逻辑操作符

逻辑操作符	说明
&	与
&&	只是用于标量，表示“与”
|	或
||	只是用于标量，表示“或”
~	非
xor	异或

例：

>> a=[1,2,-3,0,0];

>> b=[0,1,0,2,0];

>> a&b

 

ans =

 

     0     1     0     0     0

 

>> a|b

 

ans =

 

     1     1     1     1     0

 

>> -a

 

ans =

 

    -1    -2     3     0     0

 

>> xor(a,b)

 

ans =

 

     1     0     1     1     0

（3）关系与逻辑函数

函数名称	功能介绍
xor(x)	异或运算
any(x)	如果向量x中有非0元素则返回1，否则返回0
all(x)	如果向量x中所有元素非0则返回1，否则返回0
isequal(x,y)	x和y对于元素相等时置1，否则置0
ismember(x,y)	若x元素是y是子集，相应x元素置1，否则置0

例：

>> a=[1,2,-3,0,0];

>> b=[0,1,0,2,0];

>> any(a)

 

ans =

 

     1

 

>> all(a)

 

ans =

 

     0

 

>> isequal(a,b)

 

ans =

 

     0

（4）多项式运算

函数名称	功能介绍
polyval(p,x)	计算多项式p，如果x是一个标量，则计算出多项式在x点的值；如果x是一个向量或者一个矩阵，则计算出多项式在x中所有元素上的值
[y,err]=polyval(p,x,E)	计算向量x的多项式p的值。同上，计算结果在y中，同时还根据polyfit命令给出的矩阵E返回一个误差估计向量err
polyvalm(p,A)	直接对矩阵A进行多项式计算。不是像上个命令一样对每个元素进行多项式计算，而是计算p(A)=P1An+p2An+...
poly(A)	计算矩阵A的特征多项式向量
poly(x)	给出一个长度为n+1的向量，其中的元素是次数为n的多项式的系数。这个多项式的根是长度为n的向量x中的元素
compan(p)	计算带有系数p的多项式的友矩阵A,这个矩阵的特征多项式为p
roots(p)	计算特征多项式p的根，是一个长度为n的向量，也就是方程p(x)=0的解。表达式poly（roots(p)）=p为真，结果可以是复数
conv(p,q)	计算多项式p和q的乘积，也可以认为是p和q的卷积
[k,r]=deconv(p,q)	计算多项式p除q。k是商多项式，r是残多项式。这个计算等价于p和q的逆卷积

例：给定两个多项式和。试进行以下计算：

（1）计算多项式在x=1处的值。

（2）两个多项式相乘，得到一个新的多项式。

（3）求多项式的根。

解：

>> p2=[2 3 -5];

>> p3=[3 0 0 -4];

>> var_valuel=polyval(p2,1)

 

var_valuel =

 

     0

 

>> var_value2=polyval(p3,1)

 

var_value2 =

 

    -1

 

>> p5=conv(p2,p3)

 

p5 =

 

     6     9   -15    -8   -12    20

>> roots2=roots(p2)

 

roots2 =

 

   -2.5000

    1.0000

 

>> roots3=roots(p3)

 

roots3 =

 

  -0.5503 + 0.9532i

  -0.5503 - 0.9532i

   1.1006