小波分析的理解

　　小波变换是克服其他信号处理技术缺陷的一种分析信号的方法。

　　小波由一族小波基函数构成，它可以描述信号时间（空间）和频率（尺度）域的局部特性。采用小波分析最大优点是可对信号进行实施局部分析，可在任意的时间或空间域中分析信号。小波分析具有发现其他信号分析方法所不能识别的、隐藏于数据之中的表现结构特性的信息，而这些特性对机械故障和材料的损伤等识别是尤为重要的。如何选择小波基函数目前还没有一个理论标准，常用的小波函数有 Haar、 Daubechies(dbN)、 Morlet、 Meryer、Symlet、Coiflet、Biorthogonal 小波等15种。

　　但是小波变换的小波系数为如何选择小波基函数提供了依据。小波变换后的系数比较大，就表明了小波和信号的波形相似程度较大；反之则比较小。  另外还要根据信号处理的目的来决定尺度的大小。如果小波变换仅仅反映信号整体的近似特征，往往选用较大的尺度；反映信号细节的变换则选用尺度不大的小波。由于小波函数家族成员较多，进行小波变换目的各异，目前没有一个通用的标准。
    根据实际运用的经验，Morlet小波应用领域较广，可以用于信号表示和分类、图像识别特征提取；墨西哥草帽小波用于系统识别；样条小波用于材料探伤；Shannon正交基用于差
分方程求解。

 现在对小波分解层数与尺度的关系作如下解释：

      是不是小波以一个尺度分解一次就是小波进行一层的分解？
      比如：[C,L]=wavedec(X,N,’wname’)中，N为尺度，若为1，就是进行单尺度分解，也就是分解一层。    但是W=CWT(X,[2:2:128],’wname’,’plot’)的分解尺度又是从2～128以2为步进的，这里的“分解尺度”跟上面那个“尺度”的意思一样吗？
      [C,L]=wavedec(X,N,’wname’)中的N为分解层数, 不是尺度,’以wname’是DB小波为例, 如DB4, 4为消失矩,则一般滤波器长度为8, 阶数为7.
     wavedec针对于离散,CWT是连续的。
       多尺度又是怎么理解的呢？
      多尺度的理解:  如将0-pi定义为空间V0,  经过一级分解之后V0被分成0-pi/2的低频子空间V1和pi/2-pi的高频子空间W1,  然后一直分下去….得到 VJ+WJ+….W2+W1.    因为VJ和WJ是正交的空间, 且各W子空间也是相互正交的.  所以分解得到了是相互不包含的多个频域区间,这就是多分辩率分析, 即多尺度分析.
      当然多分辨率分析是有严格数学定义的,但完全可以从数字滤波器角度理解它.当然,你的泛函学的不错,也可以从函数空间角度理解.

       是不是说分解到W3、W2、W1、V3就是三尺度分解？
       简单的说尺度就是频率，不过是反比的关系．确定尺度关键还要考虑你要分析信号的采样频率大小，因为根据采样频率大小才能确定你的分析频率是多少．（采样定理）．然后再确定你到底分多少层．

       假如我这有一个10hz和50hz的正弦混合信号，采样频率是500hz，是不是就可以推断出10hz和50hz各自对应的尺度了呢？我的意思是，是不是有一个频率和尺度的换算公式？
       实际频率＝小波中心频率×采样频率/尺度

         在小波分解中，若将信号中的最高频率成分看作是1，则各层小波小波分解便是带通或低通滤波器，且各层所占的具体频带为（三层分解）a1:0~0.5 d1: 0.5~1; a2:0~0.25 d2: 0.25~0.5; a3: 0~0.125; d3:0.125~0.25    

 

　　可以这样理解吗？如果我要得到频率为0.125~0.25的信号信息，是不是直接对d3的分解系数直接重构之后就是时域信息了？这样感觉把多层分解纯粹当作滤波器来用了，又怎么是多分辨分析？？怎样把时频信息同时表达出来？？
       这个问题非常好，我刚开始的时候也是被这个问题困惑住了，咱们确实是把它当成了滤波器来用了，也就是说我们只看重了小波分析的频域局部化的特性。但是很多人都忽略其时域局部化特性，因为小波是变时频分析的方法，根据测不准原理如果带宽大，则时窗宽度就要小。那么也就意味着如果我们要利用其时域局部化特性就得在时宽小的分解层数下研究，也就是低尺度下。这样我们就可以更容易看出信号在该段时间内的细微变化，但是就产生一个问题，这一段的频率带很宽，频率局部化就体现不出来了。
       对d3进行单支重构就可以得到0.125－0.25的信号了，当然频域信息可能保存的比较好，
但如果小波基不是对称的话，其相位信息会失真。

      小波变换主要也是用在高频特征提取上。

      层数不是尺度，小波包分解中，N应该是层数，个人理解对应尺度应该是2^N

     小波分解的尺度为a，分解层次为j。   如果是连续小波分解尺度即为a。离散小波分解尺度严格意义上来说为a＝2^j,在很多书上就直接将j称为尺度，因为一个j就对应者一个尺度a。其实两者是统一的。

小波基：一般从线性相位，消失矩，相似性，紧支撑等来选择。

Daubechies小波基的构造
%  此程序实现构造小波基
%  periodic_wavelet.m
function ss=periodic_wavelet;
clear;clc;
% global MOMENT;  %  消失矩阶数
% global LEFT_SCALET;  %  尺度函数左支撑区间
% global RIGHT_SCALET;  %  尺度函数右支撑区间
% global LEFT_BASIS;  %  小波基函数左支撑区间
% global RIGHT_BASIS;  %  小波基函数右支撑区间
% global MIN_STEP;  %  最小离散步长
% global LEVEL;  %  计算需要的层数(离散精度）
% global MAX_LEVEL;  %  周期小波最大计算层数

[s2,h]=scale_integer;
[test,h]=scalet_stretch(s2,h);
wave_base=wavelet(test,h);
ss=periodic_waveletbasis(wave_base);
 

function [s2,h]=scale_integer;
%  本函数实现求解小波尺度函数离散整数点的值
%  sacle_integer.m
MOMENT=10;  %  消失矩阶数
LEFT_SCALET=0;  %  尺度函数左支撑区间
RIGHT_SCALET=2*MOMENT-1;  %  尺度函数右支撑区间
LEFT_BASIS=1-MOMENT;    %  小波基函数左支撑区间
RIGHT_BASIS=MOMENT;     %  小波基函数右支撑区间
MIN_STEP=1/512;          %  最小离散步长
LEVEL=-log2(MIN_STEP);  %  计算需要的层数(离散精度）
MAX_LEVEL=8;  %  周期小波最大计算层数

h=wfilters(‘db10’,’r’);  %  滤波器系数
h=h*sqrt(2); % FI(T)=SQRT(2)*SUM(H(N)*FI(2T-N)) N=0:2*MOMENT-1;
for i=LEFT_SCALET+1:RIGHT_SCALET-1
    for j=LEFT_SCALET+1:RIGHT_SCALET-1
       k=2*i-j+1;
       if (k>=1&k<=RIGHT_SCALET+1)
       a(i,j)=h(k);  %  矩阵系数矩阵
       else
       a(i,j)=0;
       end
    end
end
[s,w]=eig(a);  %  求特征向量，解的基
s1=s(:,1);
s2=[0;s1/sum(s1);0]; %  根据条件SUM(FI(T))=1,求解;
 
 
%  本函数实现尺度函数经伸缩后的离散值
%  scalet_stretch.m
function [s2,h]=scalet_stretch(s2,h);
MOMENT=10;  %  消失矩阶数
LEFT_SCALET=0;  %  尺度函数左支撑区间
RIGHT_SCALET=2*MOMENT-1;  %  尺度函数右支撑区间
LEFT_BASIS=1-MOMENT;  %  小波基函数左支撑区间
RIGHT_BASIS=MOMENT;  %  小波基函数右支撑区间
MIN_STEP=1/512;  %  最小离散步长
LEVEL=-log2(MIN_STEP);  %  计算需要的层数(离散精度）
MAX_LEVEL=8;  %  周期小波最大计算层数

for j=1:LEVEL  %  需要计算到尺度函数的层数
   t=0;
   for i=1:2:2*length(s2)-3  %  需要计算的离散点取值（0，1，2，3 -> 1/2, 3/2, 5/2)
      t=t+1;
      fi(t)=0;
      for n=LEFT_SCALET:RIGHT_SCALET;  % 低通滤波器冲击响应紧支撑判断
          if ((i/2^(j-1)-n)>=LEFT_SCALET&(i/2^(j-1)-n)<=RIGHT_SCALET) %  小波尺度函数紧支撑判断
            fi(t)=fi(t)+h(n+1)*s2(i-n*2^(j-1)+1);  %  反复应用双尺度方程求解
          end
      end
   end
   clear s
   n1=length(s2);
   n2=length(fi);
   for i=1:length(s2)+length(fi)  %  变换后的矩阵长度
      if (mod(i,2)==1)
      s(i)=s2((i+1)/2);  %  矩阵奇数下标为小波上一层(0,1,2,3)离散值
      else
      s(i)=fi(i/2);  %  矩阵偶数下标为小波下一层(1/2,3/2,5/2)(经过伸缩变换后)的离散值
      end
   end
   s2=s;
end
 
 

%  采用双尺度方程求解小波基函数 PSI(T)
%  wavelet.m
function wave_base=wavelet(test,h);
MOMENT=10;  %  消失矩阶数
LEFT_SCALET=0;  %  尺度函数左支撑区间
RIGHT_SCALET=2*MOMENT-1;  %  尺度函数右支撑区间
LEFT_BASIS=1-MOMENT;  %  小波基函数左支撑区间
RIGHT_BASIS=MOMENT;  %  小波基函数右支撑区间
MIN_STEP=1/512;  %  最小离散步长
LEVEL=-log2(MIN_STEP);  %  计算需要的层数(离散精度）
MAX_LEVEL=8;  %  周期小波最大计算层数

i=0;
for t=LEFT_BASIS:MIN_STEP:RIGHT_BASIS;  %  小波基支撑长度
    s=0;
    for n=1-RIGHT_SCALET:1-LEFT_SCALET  %  g(n)取值范围
        if((2*t-n)>=LEFT_SCALET&(2*t-n)<=RIGHT_SCALET)  %  尺度函数判断
          s=s+h(1-n+1)*(-1)^(n)*test((2*t-n)/MIN_STEP+1);  %  计算任意精度的小波基函数值 
        end
    end
    i=i+1;
    wave_base(i)=s;
end

 

 

 

 

 

 

 

一维数字滤波器filter():
        Y=filter(B, A, X)   由传递函数模型向量B、A描述的滤波器对向量X中的元素进行滤波，并将结果数据存放在向量Y中。
      [Y, Zf]=filter(B, A, X, Zi)   给出了滤波器延时的初始和终止条件Zf和Zi。
例子：
        人体心电信号在测量过程中往往受到工业高频干扰，所以必须经过低通滤波处理后，才能判断心脏功能的有用信息。下面给出一实际心电图信号采样序列样本x(n)，其中存在高频干扰。在试验中以x(n)作为输入序列，滤除其中的干扰成分。
{ x(n) } = {-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,
                 -2,-4,8,12,12,10,6,6,4,0,0,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0}
Matlab程序设计如下：
            X=[-4,-2,0,-4,-6,-4,-2,-4,-6,-6,-4,-4,-6,-6,-2,6,12,8,0,-16,-38,-60,-84,-90,-66,-32,-4,-2,-4,8,12,12,10,6,6,4,0,0,0,0,0,-2,-2,0,0,-2,-2,-2,-2,0];
               figure;
           plot(X);
           xlabel(‘时间‘);
           ylabel(‘幅值‘);
           wp=40;   ws=50;  rp=0.5;  rs=40;   Fs=200;
           [N, Wn] = buttord(wp/(Fs/2), ws/(Fs/2), rp, rs);
           [b, a]=butter(N, Wn);
           figure;
           [H, W]=freqz(b, a);
           plot(W*Fs/(2*pi), abs(H));   grid;
           xlabel(‘频率/Hz’);
           ylabel(‘幅值‘);
           Y=filter(b,a,X);
           figure
           plot(Y)
           xlabel(‘时间‘);
           ylabel(‘幅值‘);
           figure
           psd(X, [ ],200);
           figure
           psd(Y, [ ],200);

      end;

分析这段程序可知包括以下几部分：
       （1）首先绘制原始数据的图形；
       （2）设计一个Butterworth低通滤波器并绘制出它的幅频响应曲线；
       （3）用设计的滤波器对原数据进行滤波；
       （4）绘制滤波以后的数据图形；
       （5）绘制原数据功率谱图形；
       （6）绘制滤波以后数据功率谱图形。

       滤波器的主要目的是按照设计者的目的，突出或抑制一些频段。在本程序中，设计了一个低通滤波器，主要是抑制高频段突出低频段；在心电图信号分析中，要滤除工业高频干扰，突出低频部分.

 

　　有时某些信号容易受到噪声污染，导致无法直接辨别信号的发展趋势。  由于信号的发展趋势往往代表信号的低频部分，因此通过信号的多尺度分解，在分解的低频系数中可以观察到信号的发展趋势。

　　由于噪声的污染，从原始信号x中无法观察信号的发展趋势。通过进行五尺度的小波分解，在小波分解的低频系数重构中可以明显地看到原始信号的发展趋势。这是因为信号的发展趋势往往是信号的低频成分，在小波变换中对应着最大尺度小波变换的低频系数。此外还可以在低频中理解它，在进行低频成分的尺度分解时，随着分解层数的增加，它所含的高频成分会随之减少，因此随着尺度的增加，更多高频的信号被滤掉，可以看到信号的发展趋势。

 

1.监测信号的自相似性
       直观上讲，小波分解系数表示了信号与小波之间的“相似指数”，如果相似程度越高，则相似指数越大。因此如果一个信号的不同的尺度之间相似，则小波系数在不同的尺度上也应该相似。因此可以通过小波分解检测信号的自相似性，即检测信号的分形特征。实践表明，通过小波分解可以很好地研究信号或图像的分形特征。
       下面通过一个简单的例子来说明小波分析在检测信号自相似性中的应用，待检测的信号是经过反复迭代生成的信号，因此具有自相似性。

       程序代码如下：
       load vonkoch;
       x=vonkoch;
       subplot(211);
       plot(x);
       title(‘原始信号‘);
       subplot(212);
       %进行一维连续小波变换
      f=cwt(x,[2:2:128],’coif3’,’plot’);
     从图中可以看出分解后的小波系数在许多尺度上看上去都非常相似。

2.信号的奇异性检测
       信号的突变点和奇异点等不规则部分通常包含重要信息。
       一般信号的奇异性分为两种情况：（1）信号在某一时刻其幅值发生突变，引起信号的非连续，这种类型的突变称为第一类型的间断点；   （2）信号在外观上很光滑，幅值没有发生突变，但是信号的一阶微分有突变发生且一阶微分不连续，这种类型的突变称为第二类型的间断点。
       应用小波分析可以检测出信号中的突变点的位置、类型以及变化的幅度。下面介绍小波分析在信号奇异性检测中的应用。

      （1）第一类型间断点的检测
       下面举例说明小波分析用于检测第一类型的间断点。

 
       在本例中，信号的不连续是由于低频特征的正弦信号在后半部分突然有高频特征的正弦信号加入，首先利用傅里叶变换分析对信号在频域进行分析，发现无检测突变点，接着利用小波分析进行分析，结果证明它能够准确地检测出了信号幅值突变的位置，即高频信号加入的时间点。
    
       程序代码如下：
       load  freqbrk;
       x=freqbrk;
       
      %对信号进行傅里叶变换
       f=fft(x,1024);
       f=abs(f);
      
      figure;
      subplot(211);
      plot(x);
      subplot(212);
      plot(f);

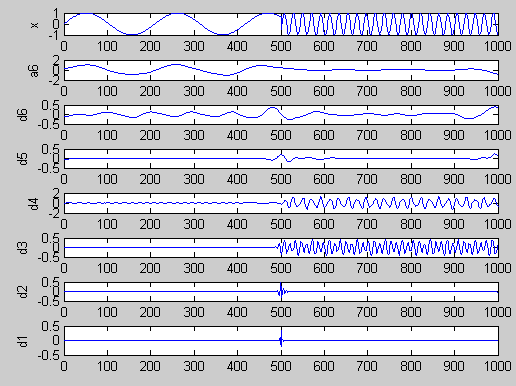
      %使用db6小波进行6层分解
       [c,l]=wavedec(x,6,’db6’);
       figure(2);
      subplot(811);
      plot(x);
      ylabel(‘x’);
   %对分解的第六层低频系数进行重构
     a=wrcoef(‘a’,c,l,’db6’,6);
     subplot(812);
     plot(a);
     ylabel(‘a6’);
     for i=1:6
                %对分解的第6层到第1层的高频系数分别进行重构
                d=wrcoef(‘d’,c,l,’db6’,7-i);
                subplot(8,1,i+2);
                plot(d);
                ylabel([‘d’,num2str(7-i)]);
   end

 

        由图中可以看出，由于傅里叶变换不具有时间分辨力，因此无法检测信号的间断点。而在小波分析的图中，在信号的小波分解的第一层高频系数d1和第二层高频系数d2中，可以非常清楚地观察到信号的不连续点，用db1小波比用db6小波要好。
       这个例子也表明小波分析在检测信号的奇异点时具有傅里叶变换无法比拟的优越性，利用小波分析可以精确地检测出信号的突变点。

      在信号处理中，信号中通常都包含噪声，而噪声的存在增加了辨别信号不连续点的难度。一般来说，如果信号小波分解的第一层能够估计出噪声的大体位置，则信号的间断点就能够在小波分解的更深层次上表现出来。

 

下面通过例子说明如何应用小波分析识别某一频率区间上的信号：

 

 

        在本例中，使用小波分析一个由三个不同频率的正弦信号叠加的信号，看是否能将这三个正弦信号区分开来，结果证明小波分析可以很好地识别某一频率区间的信号。

        程序代码如下：
        load sumsin;
        x=sumsin;
       figure;
       subplot(611);
       plot(x);
       ylabel(‘x’);
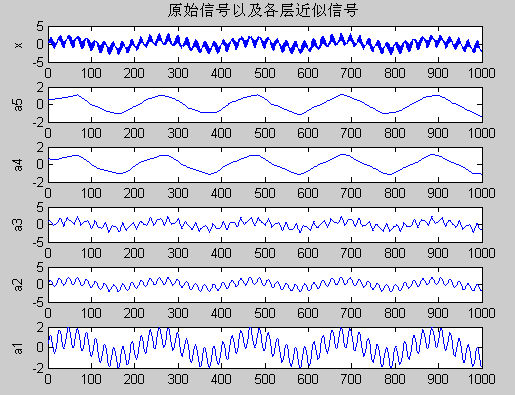
       title(‘原始信号以及各层近似信号‘);
      
      %使用db3小波进行5层分解
       [c,l]=wavedec(x,5,’db3’);
       for i=1:5
                %对分解的第5层到第1层的低频系数分别进行重构
                a=wrcoef(‘a’,c,l,’db3’,6-i);
                subplot(6,1,i+1);
                plot(a);
                ylabel([‘a’,num2str(6-i)]);
       end
 

       figure;
       subplot(611)
       plot(x);
       ylabel(‘x’)
       for i=1:5
              %对分解的第5层到第1层的高频系数进行重构
               d=wrcoef(‘d’,c,l,’db3’,6-i);
               subplot(6,1,i+1);
               plot(d);
               ylabel([‘d’,num2str(6-i)]);
       end

 

 

分析：
       在本例中，该信号是由周期分别为200、20、2的信号组成的，它们的采样周期均为1，为方便起见，在此分别称为低频、中频和高频的正弦信号。从图中可以看出，低频、中频和高频信号分别对应于分解的近似信号a4、细节信号d4以及细节信号d1。