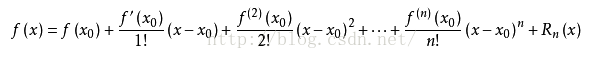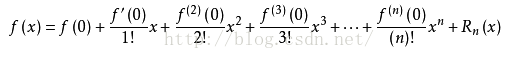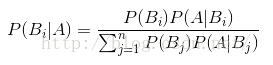1.机器学习与微积分
注:以下内容整理于七月算法2016年4月班培训讲义,详见: http://www.julyedu.com/
重点摘要:
机器学习简介
高等数学
概率论
一、机器学习简介
1.机器学习是什么?
计算机从已有数据中学习出规律和模式,在新数据上做出预测。
2.学习 = 在某项任务上总结与积攒经验,即积累知识
a) 在任务T上提升
b) 用P作为评估标准
c) 基于经验E
例如:中国象棋
a) 任务T:下中国象棋
b) 性能目标P:比赛中击败对手的百分比
c) 训练经验E:与自己对弈,或者参考棋谱自学习
3.机器学习分类:
a) 监督学习:输入数据有标签,即针对给定的特征,必须有标准答案。
*分类:标准答案是离散的,比如电影类型
*回归:标准答案是连续的,比如数据库表空间使用率预测、房价预测
b) 无监督学习:聚类,输入数据没有标签。例如:新闻分类
c) 强化学习:动态系统或机器人控制,行为认知启发
二、高等数学:
1.极限存在准则Ⅰ:夹逼定理
a) 当x∈U(x0,r)时,g(x)<=f(x)<=h(x),
b) 当x→x0时,limg(x)=A,limh(x)=A,
那么,当x→x0时,limf(x)存在且等于A
应用:当x趋近于0时,sinx/x的极限为1
2.极限存在准则Ⅱ:单调有界数列必有极限
3.导数:通过极限进行定义,换言之,导数也是极限
a) 定义
设函数y=f(x)在点x0的某邻域内有定义,当自变量x取得增量Δx(x0+Δx仍在邻域内),相应地函数取得增量Δy=f(x0+Δx)-f(x0),
如果当Δx→0时,Δy/Δx的极限存在,则称函数y=f(x)在x0处可导。
b) 一阶导数:斜率,反应曲线变化的快慢
应用:求函数的极值
驻点:一阶导数为0的点,驻点是极值点的必要而非充分条件。
极值点:若某点的两侧一阶导数变号,则该点为极值点
c) 二阶导数:反应斜率变化快慢,表征曲线的凸凹性
凸凹性:若二阶导数大于0,则曲线是凸的,否则是凹的。(注意:该定义与高等数学教材上的定义相反)
拐点:若某点的两个二阶导数变号,则该点为拐点。二阶导数等于0是判断某点是否是拐点的必要非充分条件。
d) 常用函数的导数(略)
4.泰勒公式:将复杂函数用一个关于(x-x0)的n次多项式函数近似化
即对于一个复杂的函数f(x),我们要找到一个多项式函数g(x),该多项式函数是一个关于(x-x0)的n次多项式函数,使得f(x)≈g(x),该怎么做?
我们设 g(x) = a0 + a1(x-x0) + a2(x-x0)^2 + ... + an(x-x0)^n
然后,怎样求系数a0、a1...an呢?
答案是,分别求f(x)和g(x)的零阶导数(没错,就是让f(x)=g(x)的意思)、一阶导数、二阶导数、三阶导数直到n阶导数,分别让它们相等即可。
泰勒公式中值定理:若f(x)在含有x0的某开区间(a,b)内具有直到n+1阶的导数,则当x∈(a,b)时,有
麦克劳林公式:当x0等于0时,上述公式即为麦克劳林公式
应用:
数值计算:sin(x)
考察基尼系数的图像、熵、分类误差率三者之间的关系
5.方向导数:偏导数反应的函数沿坐标轴方向的变化率。方向导数反应的是函数f(x,y)在沿方向l的变化率。
在点(x0,y0)处的方向导数=fx(x0,y0)*cosα+fy(x0,y0)*cosβ (其中,cosα和cosβ为方向l的方向余弦,fx(x0,y0)和fy(x0,y0)分别为f(x,y)对x和y的偏导数)
6.梯度
设z=F(x,y),则在点P(x0,y0)的向量(Fx(x0,y0),Fy(x0,y0))为该点的梯度。
记作:gradF(x0,y0)=Fx(x0,y0)*i+Fy(x0,y0)*j (i、j为沿坐标轴方向的单位向量)
7.沿梯度的方向是函数在该点的方向导数取得最大值的方向,梯度的模等于方向导数的最大值。
8.凸函数:二阶导数大于0
若f是凸函数,则f(θx1+(1-θ)x2) <= θf(x1)+(1-θ)f(x2)
三、概率论:
1.随机试验
a) 相同条件下可重复进行
b) 试验前可明确试验的所有可能
c) 试验前不能确定哪一个结果会出现
2.随机变量
设随机试验的样本空间为S={e},X=X(e)是定义在样本空间S上的实值单值函数,称X=X(e)为随机变量
3.分布函数
设X是一个随机变量,x是任意实数,函数 F(x)=P{X<=x},-∞
b) 0<=F(x)<=1
c) 若F(x)可导,其导函数称为概率密度函数
4.古典概型
a) 样本有限:样本空间中只包含有限个元素
b) 等可能:每个基本事件发生的可能性相同
5.概率公式
加法公式:p(A+B)=p(A)+p(B)-p(AB)
减法公式:p(A-B)=p(A)-p(AB)
乘法公式:P(AB)=p(A)*p(B|A)
全概率公式:p(A)=sum(p(A|Bi)*p(Bi))
贝叶斯公式:p(Bi|A)=p(Bi)*p(A|Bi)/sum(p(A|Bj)*p(Bj)) (Bj为样本空间的一个划分,j=1,2,3...n)
6.频率学派与贝叶斯学派
7.先验概率和后验概率
贝叶斯公式
给定某系统的若干样本X,计算该系统的参数θ,即P(θ|X)=P(θ)*P(X|θ)/P(X)
* P(θ):在没有数据支持下,θ发生的概率:先验概率
* P(θ|X):在给定数据X的情况下,θ发生的概率:后验概率
* P(X|θ):给定某参数θ的概率分布:似然函数
可参考:http://ask.julyedu.com/question/150
8.概率分布
a) 0-1分布
随机变量X只取0和1两个值,P(X=1)=p
E(X)=p
D(X)=p(1-p)
b)二项分布
设试验E值可能取两种结果,P(A)=p(0
E(X)=np
D(X)=np(1-p)
c)泊松分布
设随机变量X所有可能的取值为0,1,2....取各个值得概率为P(X=k)=λ^k*e^(-λ)/(k!),记作 X~π(λ)
E(X)=λ
D(X)=λ
d)均匀分布
若连续性随机变量X具有概率密度
f(x)=1/(b-a) (a
E(X)=(a+b)/2
D(X)=(b-a)^2/12
e)指数分布:具有无记忆性
若连续性随机变量X的概率密度为
f(x)=λe^(-λx) (x>0,x取其他值时f(x)为0)
其中λ>0为常数,则称X服从参数λ的指数分布,记作X~E(λ)
E(X)=1/λ
D(X)=1/λ^2
f) 正态分布
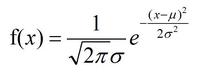
E(X)=μ
D(X)=σ^2
9.Sigmoid函数
f(x)=1/(1+e^(-x))