MATLAB-模型模糊神经网络预测控制demo

减法聚类方法从数据生成FIS结构 genfis2

tripdata
figure,plot(datin)
a=genfis2(datin,datout,0.45);
figure,plotfis(a);
figure
fuzout=evalfis(datin,a);
subplot(2,1,1)
plot(datin)
subplot(2,1,2)
plot([datout fuzout])
figure,plot(datout,fuzout,'bx',[0 10],[0 10],'r:')
xlabel('Actual Value')
ylabel('Predicted Value')
axis square

chkfuzout=evalfis(chkdatin,a);%未定义chkdatin
figure,plot(chkdatout,chkfuzout,'bx',[0 10],[0 10],'r:')
axis square
xlabel('Actual Value')
ylabel('Predicted Value')

---

genfis2 使用减法聚类方法从数据生成FIS结构
fismat = genfis2(Xin,Xout,radii)
Xin是一个矩阵，它的每一行包含一个数据点的输入值；Xout是一个矩阵，它的每一行包含一个数据点的输出值；randi是一个向量，它指定一个聚类中心在一个数据维上作用的范围，这里假定数据位于一个单位超立方体内

---

genfis1 不使用数据聚类方法从数据生成FIS结构
fismat = genfis1(data)
genfis1为an fis训练生成一个Sugeno型作为初始条件的FIS结构（初始隶属函数）

---

plotfis(fismat)
此函数显示由fismat指定的一个FIS的高层方框图，输入和它们的隶属函数出现在结构特征图的左边，同时输出和它们的隶属函数出现在结构特征图的右边。

---

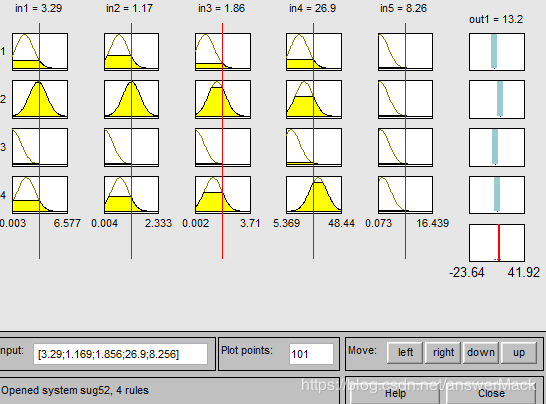
evalfis 完成模糊推理计算
output= evalfis(input,fismat)
input：指定输入值的一个数或一个矩阵，如果输入是一个M×N矩阵，其中N是输入变量数，那么evalfis使用 input的每一行作为一个输入向量，并且为变量output返回M×L矩阵，该矩阵每一行是一个向量并且L是输出变量数；
fismat：要计算的一个FIS结构；

---

自适应神经模糊推理系统DEMO：anfis

anfis:Adaptive Neural Network Based Fuzzy Interference System

% The Mackey-Glass time-delay differential equation is defined by dx(t)/dt = 0.2x(t-tau)/(1+x(t-tau)^10) - 0.1x(t)
% When x(0) = 1.2 and tau = 17, we have a non-periodic and non-convergent time series that is very sensitive to initial conditions. (We assume x(t) = 0 when t < 0.) 

load mgdata.dat%Mackey-Glass 时间序列
a=mgdata;
time = a(:, 1);
ts = a(:, 2);
figure,plot(time, ts);
xlabel('Time (sec)'); ylabel('x(t)');
title('Mackey-Glass Chaotic Time Series');

% Now we want to build an ANFIS that can predict x(t+6) from the past values of this time series, that is, x(t-18), x(t-12), x(t-6), and x(t). Therefore the training data format is [x(t-18), x(t-12), x(t-6), x(t); x(t+6]
% From t = 118 to 1117, we collect 1000 data pairs of the above format. The first 500 are used for training while the others are used for checking. The plot shows the segment of the time series where data pairs were extracted from. 

trn_data = zeros(500, 5);
chk_data = zeros(500, 5);

% prepare training data
start = 101;
trn_data(:, 1) = ts(start:start+500-1);
start = start + 6;
trn_data(:, 2) = ts(start:start+500-1);
start = start + 6;
trn_data(:, 3) = ts(start:start+500-1);
start = start + 6;
trn_data(:, 4) = ts(start:start+500-1);
start = start + 6;
trn_data(:, 5) = ts(start:start+500-1);

% prepare checking data
start = 601;
chk_data(:, 1) = ts(start:start+500-1);
start = start + 6;
chk_data(:, 2) = ts(start:start+500-1);
start = start + 6;
chk_data(:, 3) = ts(start:start+500-1);
start = start + 6;
chk_data(:, 4) = ts(start:start+500-1);
start = start + 6;
chk_data(:, 5) = ts(start:start+500-1);

index = 118:1117+1; % ts starts with t = 0
figure,plot(time(index), ts(index));
axis([min(time(index)) max(time(index)) min(ts(index)) max(ts(index))]);
xlabel('Time (sec)'); ylabel('x(t)');
title('Mackey-Glass Chaotic Time Series');

% We use GENFIS1 to generate an initial FIS matrix from training data. The command is quite simple since default values for MF number (2) and MF type ('gbellmf') are used: 

fismat = genfis1(trn_data);

% The initial MFs for training are shown in the plots.
figure
for input_index=1:4,
    subplot(2,2,input_index)
    [x,y]=plotmf(fismat,'input',input_index);
    plot(x,y)
    axis([-inf inf 0 1.2]);
    xlabel(['Input ' int2str(input_index)]);
end

% There are 2^4 = 16 rules in the generated FIS matrix and the number of fitting parameters is 108, including 24 nonlinear parameters and 80 linear parameters. This is a proper balance between number of fitting parameters and number of training data (500). The ANFIS command looks like this: >> [trn_fismat,trn_error] = anfis(trn_data, fismat,[],[],chk_data)
% To save time, we will load the training results directly. After ten epochs of training, the final MFs are shown in the plots. Note that these MFs after training do not change drastically. Obviously most of the fitting is done by the linear parameters while the nonlinear parameters are mostly for fine- tuning for further improvement. 

%anfis 自适应神经模糊推理系统 [trn_fismat,trn_error] = anfis(trn_data, fismat,[],[],chk_data)
% load training results
load mganfis

% plot final MF's on x, y, z, u
figure
for input_index=1:4,
    subplot(2,2,input_index)
    [x,y]=plotmf(trn_fismat,'input',input_index);
    plot(x,y)
    axis([-inf inf 0 1.2]);
    xlabel(['Input ' int2str(input_index)]);
end

% Error curves     This plot displays error curves for both training and checking data. Note that the training error is higher than the checking error. This phenomenon is not uncommon in ANFIS learning or nonlinear regression in general; it could indicate that the training process is not close to finished yet. 

% error curves plot
epoch_n = 10;
tmp = [trn_error chk_error];
figure,plot(tmp);
hold on; plot(tmp, 'o'); hold off;
xlabel('Epochs');
ylabel('RMSE (Root Mean Squared Error)');
title('Error Curves');
axis([0 epoch_n min(tmp(:)) max(tmp(:))]);

% Comparisons    This plot shows the original time series and the one predicted by ANFIS. The difference is so tiny that it is impossible to tell one from another by eye inspection. That is why you probably see only the ANFIS prediction curve. The prediction errors must be viewed on another scale. 

input = [trn_data(:, 1:4); chk_data(:, 1:4)];
anfis_output = evalfis(input, trn_fismat);
index = 125:1124;
figure,plot(time(index), [ts(index) anfis_output]);
xlabel('Time (sec)');

% Prediction errors of ANFIS      Prediction error of ANFIS is shown here. Note that the scale is about a hundredth of the scale of the previous plot. Remember that we have only 10 epochs of training in this case; better performance is expected if we have extensive training. 

diff = ts(index)-anfis_output;
figure,plot(time(index), diff);
xlabel('Time (sec)');
title('ANFIS Prediction Errors');

预测误差：

预测结果：

参考

模糊函数介绍及解释：
详细解释：https://blog.csdn.net/MonMama/article/details/91040016
简单解释：https://blog.csdn.net/qq_26093511/article/details/51872476
参考文章：https://wenku.baidu.com/view/f0c69e854028915f814dc246.html
参考书籍：《matlab控制系统应用与实例》清华大学出版社 樊京、刘叔军、盖晓华、崔世林编辑。
例程：源码CH8_3.m、CH8_4.m