机器学习基础——Adaboost
一、前言
最近吴恩达的机器学习课程已经快学习完了。作为一个转行人员,发现学习的算法还是有点少,加上这一阵看了不少同志的面试经验,发现Gradient Boosting以及相关的GBDT等算法是比较基础的。但是看了一下GB,发现这个没有具体实例,不太直观,加之看过不少人和书上的内容。Adaboost是Boosting族算法中最著名的,而且还是比较好懂的。特此总结一下。
二、Adaboost原理和Boosting
2.1 Boosting算法的起源
boost算法系列的起源来自于PAC Learnability(PAC 可学习性)。这套理论主要研究的是什么时候一个问题是可被学习的,当然也会探讨针对可学习的问题的具体的学习算法。这套理论是由Valiant提出来的,也因此,所以他获得了2010年的图灵奖。
PAC 定义了学习算法的强弱:
弱学习算法—识别错误率小于1/2(即准确率仅比随机猜测略高的学习算法)
强学习算法—识别准确率很高并能在多项式时间内完成的学习算法
同时 ,Valiant和 Kearns首次提出了PAC学习模型中弱学习算法和强学习算法的等价性问题,即任意给定仅比随机猜测略好的弱学习算法,是否可以将其提升为强学习算法?如果二者等价,那么只需找到一个比随机猜测略好的弱学习算法就可以将其提升为强学习算法 ,而不必直接去寻找很难获得的强学习算法。也就是这种猜测,让很多人去设计算法来验证PAC理论的正确性。
不过很长一段时间都没有一个切实可行的办法来实现这个理想。细节决定成败,再好的理论也需要有效的算法来执行。终于功夫不负有心人,
Schapire在1996年提出一个有效的算法真正实现了这个夙愿,它的名字叫AdaBoost。AdaBoost把多个不同的决策树用一种非随机的方式组合起来,表现出惊人的性能!第一,把决策树的准确率大大提高,可以与SVM媲美。第二,速度快,且基本不用调参数。第三,几乎不Overfitting。我估计当时Breiman和Friedman肯定高兴坏了,因为眼看着他们提出的CART正在被SVM比下去的时候,AdaBoost让决策树起死回生!Breiman情不自禁地在他的论文里赞扬AdaBoost是最好的现货方法(off-the-shelf,即“拿下了就可以用”的意思)。(这段话摘自统计学习那些事)
2.2 Boosting
Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制为:
① 先从初始训练集(Training Sample)训练得到一个基学习器(弱学习器)
② 根据基学习器的预测结果(performance)对训练样本进行调整,使得这个基学习器做错的训练样本在后续增加关注度;没做错的则降低关注度。
③ 这样,基于调整后样本来训练下一个基学习器
④ 如此反复,直到达到你所想要基学习器的数量M,然后将这M个基学习器进行加权组合(dml.tools —> sign(参考Dark_Scope的代码))
Adaboost是Boosting族中最著名的代表算法,由Freund和Schapire于1997年正式提出,其描述如下图所示(以二分类为例,类别分别用1和-1表示):

其中:1) Zm 为规范化因子,其目的是使得 wm+1,i 成为一个分布
2)当误差 ϵm <= 1/2时, αm >= 0,且 αm 随着 ϵm 的减小而增大,意味着分类误差率越小的基本分类器在最终分类器中的所占比重越大。
3) wm+1,i 是更新训练集中每一个样本的权值,用于新一轮的迭代使用。其效果是:使得误分类的样本在下次迭代中的权值增加,使得正确分类的样本在下次迭代中的权值减少。
2.3 Adaboost原理
这里采用容易理解的“加性模型”(additive model)来推导:即用基学习器的线性组合表示分类器H(x):

来最小化指数函数损失(exponential loss function)[Friedman et al., 2000]
![]()
其中 fm(xn) 就是上面的 H(x) 。 tn 为实际的label, hi(x) 为弱分类器。
我们的目标是:最小化E
假设前m-1个α和h都已经fixed了:那么
![]()
其中 w(m)n 可以看成是一个常量了,因为它里面的参数都是已知的,或者说假设为已知了。
![]()
其中 Tm 表示正确分类的集合, Mm 表示误分类的集合,这一步其实就是把上面那个式子拆开。
然后就是找 ym 了,即最小化下式:
![]()
由于代价函数(损失函数已知),我们推出 Zm 和代价函数 E (取指数损失时)关系为:
证明如下:

下面利用这个结果,来继续证明弱分类器中权重更新值为: αm=12log1−ϵmϵm


由这个式子可以容易的得到: αm=12log1−ϵmϵm 。即错误率小的弱分类器的权重更大。
三、例子
可能看到这里,还是有不少童鞋不太理解。比如:弱分类器hi是怎么构造的能使得ei尽可能小?
下面放上一个例子,李航的《统计学习方法》中最简单的例子
![]()
求解过程:初始化训练数据的权值分布,令每个权值W1i = 1/n = 0.1,其中,n = 10,i = 1,2, …, 10,然后分别对于m = 1,2,3, …等值进行迭代。
拿到这10个数据的训练样本后,根据 X 和 Y 的对应关系,要把这10个数据分为两类,一类是“1”,一类是“-1”,根据数据的特点发现:“0 1 2”这3个数据对应的类是“1”,“3 4 5”这3个数据对应的类是“-1”,“6 7 8”这3个数据对应的类是“1”,9是比较孤独的,对应类“-1”。抛开孤独的9不讲,“0 1 2”、“3 4 5”、“6 7 8”这是3类不同的数据,分别对应的类是1、-1、1,直观上推测可知,可以找到对应的数据分界点,比如2.5、5.5、8.5 将那几类数据分成两类。当然,这只是主观臆测,下面实际计算下这个过程。
第一次迭代
对于m=1,在权值分布为D1(10个数据,每个数据的权值皆初始化为0.1)的训练数据上,经过计算可得:
阈值v取2.5时误差率为0.3(x < 2.5时取1,x > 2.5时取-1,则6 7 8分错,误差率为0.3),
阈值v取5.5时误差率最低为0.4(x < 5.5时取1,x > 5.5时取-1,则3 4 5 6 7 8皆分错,误差率0.6大于0.5,不可取。故令x > 5.5时取1,x < 5.5时取-1,则0 1 2 9分错,误差率为0.4),
阈值v取8.5时误差率为0.3(x < 8.5时取1,x > 8.5时取-1,则3 4 5分错,误差率为0.3)。
所以无论阈值v取2.5,还是8.5,总得分错3个样本,故可任取其中任意一个如2.5,弄成第一个基分类器为:

可以看出:0 1 2对应的类(Y)是1,因它们本身都小于2.5,所以被h1(x)分在了相应的类“1”中,分对了。
3 4 5本身对应的类(Y)是-1,因它们本身都大于2.5,所以被h1(x)分在了相应的类“-1”中,分对了。
6 7 8本身对应类(Y)是1,却因它们本身大于2.5而被h1(x)分在了类”-1”中,所以这3个样本被分错了。
9本身对应的类(Y)是-1,因它本身大于2.5,所以被h1(x)分在了相应的类“-1”中,分对了。
从而得到h1(x)在训练数据集上的误差率(被h1(x)误分类样本“6 7 8”的权值之和)e1=P(h1(xi)≠yi) = 3*0.1 = 0.3。
然后根据误差率 e1 计算 h1 的系数。
![]()
这个 α1 代表基学习器 h1(x) 在最终的分类函数中所占的权重为0.4236。接着更新训练数据的权值分布,用于下一轮迭代。
ps:由权值更新的公式可知,每个样本的新权值是变大还是变小,取决于它是被分错还是被分正确。即如果某个样本被分错了,则 yi∗hm(xi) 为负,负负等正,结果使得整个式子变大(样本权值变大),否则变小。
第一轮迭代后,最后得到各个数据新的权值分布D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)。由此可以看出,因为样本中是数据“6 7 8”被h1(x)分错了,所以它们的权值由之前的0.1增大到0.1666,反之,其它数据皆被分正确,所以它们的权值皆由之前的0.1减小到0.0715。
分类函数
此时,得到的第一个基本分类器sign(f1(x))在训练数据集上有3个误分类点(即6 7 8)。
从上述第一轮的整个迭代过程可以看出:被误分类样本的权值之和影响误差率,误差率影响基本分类器在最终分类器中所占的权重。
第二次迭代
对于m=2,在权值分布为D2 = (0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)的训练数据上,经过计算可得:
阈值v取2.5时误差率为0.1666*3(x < 2.5时取1,x > 2.5时取-1,则6 7 8分错,误差率为0.1666*3),
阈值v取5.5时误差率最低为0.0715*4(x > 5.5时取1,x < 5.5时取-1,则0 1 2 9分错,误差率为0.0715*3 + 0.0715),
阈值v取8.5时误差率为0.0715*3(x < 8.5时取1,x > 8.5时取-1,则3 4 5分错,误差率为0.0715*3)。
所以,阈值v取8.5时误差率最低,故第二个基本分类器为:
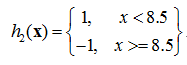
很明显,h2(x)把样本“3 4 5”分错了,根据D2可知它们的权值为0.0715, 0.0715, 0.0715,所以h2(x)在训练数据集上的误差率e2=P(G2(xi)≠yi) = 0.0715 * 3 = 0.2143。
计算h2的系数:
![]()
更新训练数据的权值分布,得到:
D3 = (0.0455, 0.0455, 0.0455, 0.1667, 0.1667, 0.01667, 0.1060, 0.1060, 0.1060, 0.0455)。被分错的样本“3 4 5”的权值变大,其它被分对的样本的权值变小。
此时,得到的第二个基本分类器sign(f2(x))在训练数据集上有3个误分类点(即3 4 5)。
f2(1) = 0.4236x1 + 0.6496x1 大于0,预测取为正类(1) 实际也为正,预测正确
f2(3) = 0.4236x(-1) + 0.6496x1 大于0,也预测取正类(1) 但是实际为负类,预测错误
第三次迭代过程得到 f3(x) ,有 sign(f3(x)) 在训练集上的误分类点为0,这里就不写了,思路和上面一样。
四、参考资料
1、 《机器学习》 周志华 p173
2、 《统计学习方法》 李航 8.3节
3、 Adaboost 算法的原理与推导
4、 AdaBoost–从原理到实现