算法篇-10-回溯法-工作分配&世界名画监视
本系列所有代码https://github.com/YIWANFENG/Algorithm-github
工作分配
n个工作分给n个人,将i工作给j号人所需费用为c[i][j],设计一算法为每人分配一工作,并且耗费最小。
算法思路分析与相关公式:
这题也是一简单的排列树问题,方式类似于旅行售货员问题,不同之处在于这里不需要判断是否有回路,所以变得更简单了。
程序源代码:
#include
#include
//工作分配问题-回溯法
//排列树
using namespace std;
class WorkAssign{
private:
intn; //n个人
int*time; //(n+1)*(n+1)矩阵,表示i分给j所需的费用
int *best_c; //最优解
int*curr_c; //当前最优分配
intcurr_t; //当前耗费
intbest_t; //最优耗费
private:
voidBacktrack(int t)
{
//第i个人
if(t>n&&curr_t(curr_c[t],curr_c[i]);
Backtrack(t+1);
swap(curr_c[t],curr_c[i]);
curr_t-= time[t*(n+1)+i];
curr_c[t]= 0;
}
}
public:
intSolve(int n_,int *time_,int *best,int max_time)
{
n = n_;
time = time_;
best_c = best;
curr_c = new int[(n+1)*(n+1)];
curr_t = 0;
best_t = max_time;
Backtrack(1);
delete []curr_c;
return best_t;
}
};
int main()
{
intn=5;
inttime_[] = {
0,0,0,0,0,0,
0,1,2,3,4,5,
0,5,1,2,3,4,
0,4,4,1,1,4,
0,4,2,4,1,5,
0,5,4,2,3,1
};
intwu[n+1];
WorkAssignwa;
cout<<"最小耗费"<
缺点分析:
在这里同样没有加限界函数,其中一限界方法同于旅行售货员问题,若当前耗费超过以求出的最优耗费,则不必搜索当前结点的子树。
世界名画监视问题
题目:
世界名画陈列馆由m×n个排列成矩形阵列的陈列室组成。为了防止名画被盗,需要在陈列室中设置警卫机器人哨位。每个警卫机器人除了监视它所在的陈列室外,还可以监视与它所在的陈列室相邻的上、下、左、右4 个陈列室。试设计一个安排警卫机器人哨位的算法,使得名画陈列馆中每一个陈列室都在警卫机器人的监视之下,且所用的警卫机器人数最少。
算法思路分析以及相关公式:
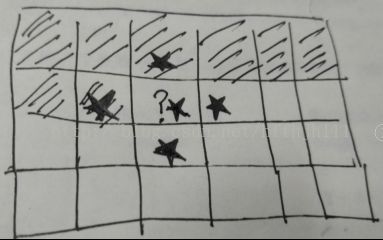
欲监视这个m*n矩阵,我们先来假设在安排第n号房间时,从0~(n-1)号房间安排完毕,即下图黑色阴影部分安排完毕,在安排?所标位置时,可安放机器人位置为五个有五角星标注的位置,经过分析可知上、左五角星不可能获得最优安排,因为他们安排后分别只能多监视1、2个房间,所以下一步应安排在中、右、下这三位置中某一个。
那么判断回溯结束即时房间全部安全,即不安全房间为0,此时应记录当前最优解与当前全局最优解比较。回溯时我们要变动对房间的监视情况,用一整数表示某房间监视情况,有一机器人监视到他就+1,此时该房间若为1则不安全房间减一,这样在回溯时取消机器人后就应考虑-1,若该房间为0则不安全房间加一。
程序源代码:
#include
//世界名画排列问题
//回溯法
//算法时间复杂度不理想啊,7*7矩阵以上复杂度陡增。
//8*8矩阵用我这电脑跑了近50分钟
using namespace std;
class Point{
public:
intx,y;
Point(intx_,int y_) {
x=x_;y=y_;
}
Point(){
x=0;y=0;
}
};
class Monitor{
private:
int*rooms; // m*n矩阵表示房间被几人监视
intm; //m行
intn; //n列
bool*robot; //m*n矩阵表示当前解的机器人安排
bool*result; //返回安排结果
intbestc; //最少机器哨位数
intcurr_c; //当前机器哨位数
intnot_safe; //当前不安全房间数
private:
voidChange(Point &t)
{
//room,not_safe与 robot变动
//中间
if(t.x>0&&t.y>0&&t.x<=m&&t.y<=n){
robot[t.x*(n+1)+t.y]= true;
rooms[t.x*(n+1)+t.y]++;
if(rooms[t.x*(n+1)+t.y]==1)not_safe--;
} else {
return;
}
//上
if(t.x-1>0&&t.y>0&&t.x-1<=m&&t.y<=n){
rooms[(t.x-1)*(n+1)+t.y]++;
if(rooms[(t.x-1)*(n+1)+t.y]==1)not_safe--;
}
//右
if(t.x>0&&t.y+1>0&&t.x<=m&&t.y+1<=n){
rooms[t.x*(n+1)+t.y+1]++;
if(rooms[t.x*(n+1)+t.y+1]==1)not_safe--;
}
//下
if(t.x+1>0&&t.y>0&&t.x+1<=m&&t.y<=n){
rooms[(t.x+1)*(n+1)+t.y]++;
if(rooms[(t.x+1)*(n+1)+t.y]==1)not_safe--;
}
//左
if(t.x>0&&t.y-1>0&&t.x<=m&&t.y-1<=n){
rooms[t.x*(n+1)+t.y-1]++;
if(rooms[t.x*(n+1)+t.y-1]==1)not_safe--;
}
}
voidRecover(Point &t)
{
//room,not_safe与 robot恢复
if(t.x>0&&t.y>0&&t.x<=m&&t.y<=n){
robot[t.x*(n+1)+t.y]= false;
rooms[t.x*(n+1)+t.y]--;
if(rooms[t.x*(n+1)+t.y]==0)not_safe++;
} else {
return;
}
//上
if(t.x-1>0&&t.y>0&&t.x-1<=m&&t.y<=n){
rooms[(t.x-1)*(n+1)+t.y]--;
if(rooms[(t.x-1)*(n+1)+t.y]==0)not_safe++;
}
//右
if(t.x>0&&t.y+1>0&&t.x<=m&&t.y+1<=n){
rooms[t.x*(n+1)+t.y+1]--;
if(rooms[t.x*(n+1)+t.y+1]==0)not_safe++;
}
//下
if(t.x+1>0&&t.y>0&&t.x+1<=m&&t.y<=n){
rooms[(t.x+1)*(n+1)+t.y]--;
if(rooms[(t.x+1)*(n+1)+t.y]==0)not_safe++;
}
//左
if(t.x>0&&t.y-1>0&&t.x<=m&&t.y-1<=n){
rooms[t.x*(n+1)+t.y-1]--;
if(rooms[t.x*(n+1)+t.y-1]==0)not_safe++;
}
}
PointFindNotSafe(Point &t)const
{
//找到一个不安全房屋
for(int i=t.x; i<=m; ++i) {
for(intj=1; j<=n; ++j) {
if(i>0&&rooms[i*(n+1)+j]==0) {
//cout<<"("<m ||t.y>n)
return;
Point x1,x2;
//(t.x,t.y)
Change(t);
curr_c++;
x1 = FindNotSafe(t);
//cout << "(" < 0 && x2.y > 0&& x2.x <= m && x2.y <= n) {
Change(x2);
curr_c++;
x1= FindNotSafe(t);
Backtrack(x1);
Recover(x2);
curr_c--;
}
//(t.x+1,t.y)
x2.x = t.x+1;
x2.y = t.y;
if (x2.x > 0 && x2.y > 0&& x2.x <= m && x2.y <= n) {
Change(x2);
curr_c++;
x1= FindNotSafe(t);
Backtrack(x1);
Recover(x2);
curr_c--;
}
}
public:
intSolve(int m_,int n_,bool *res)
{
//m_ 行 n_列 res[] 最终安排数组
//返回所需最少机器人属
m =m_; n=n_;
rooms=(int*)malloc(sizeof(int)*(n+1)*(m+1));
robot=(bool*)malloc(sizeof(bool)*(n+1)*(m+1));
for(int i=0;i<(n+1)*(m+1);++i) {
rooms[i]= 0;
robot[i]= false;
}
result = res;
bestc = m*n;
curr_c = 0;
not_safe=m*n; //当前不安全房间数
Backtrack(Point(1,1));
free(rooms);
free(robot);
return bestc;
}
};
void show(int m_,int n_,bool *res)
{
for(inti=1; i<=m_; ++i) {
for(int j=1; j<=n_; ++j) {
if(res[i*(n_+1)+j])cout<<"# ";
elsecout<<"O ";
}
cout<<'\n';
}
}
int main(int argc,char *argv[])
{
intn = 4, m = 4;
cout<< "输入房间矩阵大小行列";
cin>> m >> n;
Monitorsl;
bool*res = new bool[(n+1)*(m+1)];
cout<<"最少哨兵:"<>aa;
return0;
} 运行结果分析:
算法时间复杂度不理想啊,7*7矩阵以上复杂度陡增。
8*8矩阵用我这电脑跑了近50分钟 。优化方向应是增加一些剪枝函数加以限制。
提到过结点控制,但是我此时没有想出来。