浅析求两个数的最大公约数的三种算法

1.最大公约数（最大公因数）就是几个数公有的因数中最大的一个。
例：12与18 12的因数有1，12，2，6，3，4
18的因数有1，18，2，9，6，3
公有的因数有1，2，3，6， 所以6就是12与18的最大公约数.
而求最大公约数的方法可以总结为：

1)更相减损法：更相减损术， 出自于中国古代的《九章算术》，也是一种求最大公约数的算法。

①先判断两个数的大小，如果两数相等，则这个数本身就 是就是它的最大公约数。
②如果不相等，则用大数减去小数，然后用这个较小数与它们相减的结果相比较，如果相等，则这个差就是它们的最大公约数，而如果不相等，则继续执行②操作。

解法分析（更相减损法）：
例如： 有两个数 12 18，它们的最大公约数为6
12 = 6 * a—————–12肯定是它最大公约数的倍数
18 = 6 * b—————–18也肯定是它最大公约数的倍数
18 - 12 = 6 *(b - a)——由结果可看出它们的差值肯定也是最大公约数的倍数
12 - 6 = 6 ————-直到减数和差值相同时，则这个相同的数就是它们的最大公约数。（其原理就是用两个数相等时，它本身就是最大公约数，因为，除去第一次相减，其余的每次减法都是用减数和差值相减，当然了，这仅仅是个人的看法，感觉这样可以好理解一点）

---

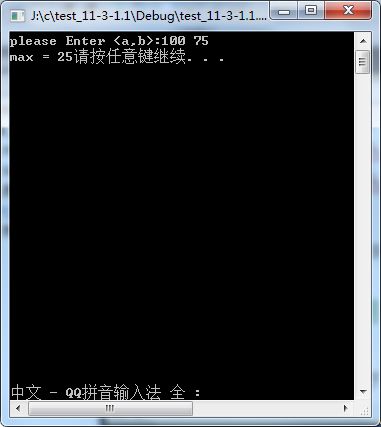
第一种方法（用更相减损法求最大公约数）：

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include

int Max_Com_Divisor(int x, int y)//用更相减损法求最大公约数
{
    while (1)//用大数减去小数并将结果保存起来
    {
        if (x > y)
        {
            x -= y;
        }
        else if(x < y)
        {
            y -= x;
        }
        else//如果两个数相等时，则这个数就是最大公约数
        {
            return x;
        }
    }
}


int main()
{
    int a = 0;
    int b = 0;
    int com_div = 0;
    printf("please Enter :");
    scanf("%d %d",&a,&b);
    com_div = Max_Com_Divisor(a,b);
    printf("max = %d",com_div);
    system("pause");
    return 0;
}

结果如下

：

第二种方法（用辗转相除法求最大公约数）：
辗转相除法， 又名欧几里得算法（Euclidean algorithm），目的是求出两个正整数的最大公约数。它是已知最古老的算法， 其可追溯至公元前300年前。

这条算法基于一个定理：两个正整数a和b（a>b），它们的最大公约数等于a除以b的余数c和b之间的最大公约数。比如10和25，25除以10商2余5，那么10和25的最大公约数，等同于10和5的最大公约数。

2)辗转相除法解法分析：
①当两个数相等时，其中任意一个就是它们的最大公约数，因为它们的余数为0；
②当两个数不相等时，用较大数除以较小数，当余数不为0时，这时
使较小数作为被除数，余数作为除数，继续 ②的操作，直至余数为0,也就是这两个数相等时，其中任一数为最大公约数。

依然是上面的例子：18和12的最大公约数6
18 = 6 * a
12 = 6 * b
18/12—–商为1—–余数为6 = 6 *1—-可以看出余数也是最大公约数的倍数
12/6——-商为2—–余数为0———–所以得到6为最大公约数

通用分析：

首先，我们先计算出a除以b的余数c，把问题转化成求出b和c的最大公约数；然后计算出b除以c的余数d，把问题转化成求出c和d的最大公约数；再然后计算出c除以d的余数e，把问题转化成求出d和e的最大公约数……

以此类推，逐渐把两个较大整数之间的运算简化成两个较小整数之间的运算，直到两个数可以整除，或者其中一个数减小到1为止。

#define _CRT_SECURE_NO_WARNINGS 1  
#include  
#include  
#include  

int Max_Com_Divisor(int x, int y)//用辗转相除法求最大公约数  
{  
    while (x * y)//当其中一个为0时，终止循环  
    {  
        if (x > y)//将较大数模较小数的结果（余数）赋给较大的值，直到两个数相等  
        {  
            x %= y;  
        }  
        else if(x < y)  
        {  
            y %= x;  
        }  
    }  
    return x > y ? x : y;  
}  


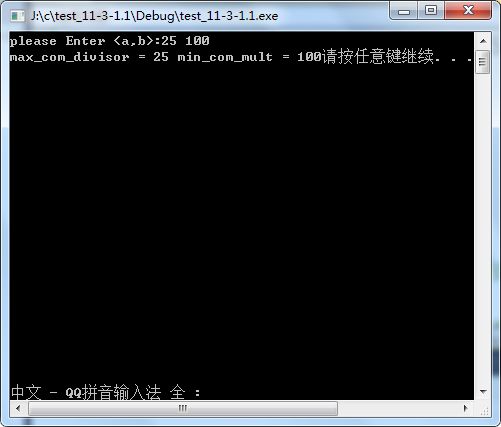
int main()  
{  
    int a = 0;  
    int b = 0;  
    int max_com_div = 0;  
    int min_com_mult = 0;  
    printf("please Enter :");  
    scanf("%d %d",&a,&b);  
    max_com_div = Max_Com_Divisor(a,b);  
    min_com_mult = (a * b)/max_com_div;//min_com_mult为最小公倍数  
    printf("max_com_divisor = %d min_com_mult = %d",\  
           max_com_div,min_com_mult);  
    system("pause");  
    return 0;  
}  

---

第三种方法：使用递归（结合辗转相除法和更相减损法的优势以及移位运算）

众所周知，移位运算的性能非常快。对于给定的正整数a和b，不难得到如下的结论。其中gcb(a,b)的意思是求a,b的最大公约数的函数

当a和b均为偶数，gcb(a,b) = 2*gcb(a/2, b/2) = 2*gcb(a>>1, b>>1)

当a为偶数，b为奇数，gcb(a,b) = gcb(a/2, b) = gcb(a>>1, b)

当a为奇数，b为偶数，gcb(a,b) = gcb(a, b/2) = gcb(a, b>>1)

当a和b均为奇数，利用更相减损术运算一次，gcb(a,b) = gcb(b, a-b)， 此时a-b的结果必然是偶数，又可以继续进行移位运算。

比如计算10和25的最大公约数的步骤如下：

（10，25）———（10>>1,25 ）————-( 5,25）
（5，25 ）———-（5，25-5 ）————（5，20）
（利用更相减损法）
（5，20）———-（5，20>>1 ）———– （5，10）
（5, 10）———-（5，10>>1 ）———– （5，5）
（5，5）———–（5，5-5）———（5，0）——-5为最大公约数
（利用更相减损法）
在两数比较小的时候，暂时看不出计算次数的优势，当两数越大，计算次数的节省就越明显。

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include

int gcd(int data1,int data2)
{
    if (data1 == data2)
    {
        return data1;
    }
    if (data1 < data2)//为了保证较大的数始终在前面，减少了代码
    {
        gcd(data2,data1);
    }
    else
    {//与1操作是为了判断奇偶
        if (!(data1 & 1) && !(data2 & 1))//两数都是偶数
        {
            return gcd(data1>>1,data2>>1)<<1;       
        }
        else if(!(data1 & 1) && (data2 & 1))//data1为偶数，data2为奇数
        {
            return gcd(data1>>1,data2);
        }
        else if((data1 & 1) && !(data2 & 1))//data1为奇数，data2为偶数
        {
            return gcd(data1,data2>>1);
        }
        else//当两个数都为奇数时，应用更相减损法
        {
            return gcd(data2,data1 - data2);
        }
    }
}

int main()
{
    int data1 = 0;
    int data2 = 0;
    int ret = 0;
    printf("Please Enter:");
    scanf("%d %d",&data1,&data2);
    ret = gcd(data1,data2);
    printf("ret : %d \n",ret);
    system("pause");
    return 0;
}

2.最小公倍数就是几个数公有的倍数中最小的一个。
6的倍数有6，12，18，24，……
4和6 公倍数 12，18……， 所以4和6的最小公倍数是12 。
如果求a和b的最小公倍数，可以先求出它们的最大公约数，最小公倍数就是 a*b/最大公约数

由于查的好多资料上面在求最大公约数时几乎没有算法的分析，只有该怎样求的方法，但是却没有深入讲解这个问题，所以为了能够深入了解算法是怎样来的，故整理了如上的解析，如果你还有更好的想法或理解，欢迎分享探讨。