MATLAB强化学习入门——五、倒立摆的DQN神经网络控制
在上一期中，使用DQN算法，我们让智能体能够顺利解决较大的网格迷宫问题。本期我们更进一步，尝试用DQN控制倒立摆。倒立摆是非常经典的控制问题，如果DQN能够有效实现倒立摆的控制，也就意味着DQN等强化学习算法适用于更复杂的动力学控制问题，即就是说，采用相似的思想，我们可以将强化学习算法用于机械臂控制、卫星姿态控制等工程问题上。
像往常一样，想要实现倒立摆的强化学习控制，我们可以把这样一个大问题拆解成几个相对独立的问题解决。第一是使用MatLab实现倒立摆的数值仿真建模；第二则是修改DQN算法，使之能够与倒立摆环境相适应；第三则是改善程序的整体框架，使它更简洁、更易于维护。
第一个问题中，倒立摆的动力学方程可以整理为常微分方程；同时，为了更好的与之前我们掌握的神经网络工具箱结合，我们使用MatLab的Ode45()函数实现动力学仿真。
第二个问题，我们需要根据倒立摆问题调整神经网络和DQN算法的相关参数，使之能够满足控制需求。这其中，神经网络的输入、输出参数需要得到调整；DQN算法中的回报(reward)需要修改；训练循环的计数方式以及训练周期等内容也需要调整。
最后，由于整个程序中加入了倒立摆的数值仿真，不仅参数和常数增多，程序也相对网格迷宫程序复杂了很多。因此，我们需要优化程序的编写，以提高程序的易读性和维护性。
一、倒立摆的数学建模
1.1 倒立摆模型的方程
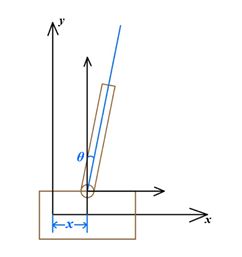
倒立摆由小车以及小车上向上铰支的摆杆组成，显然，当摆杆朝上时，这是一个可以平衡但不能稳定的系统。
小车固定在横轴上，因此在y方向上无位移，仅在x方向上有位移和速度。在水平方向上，小车受到控制力、摩擦力以及摆杆支撑力水平分量的作用。取x_c为x方向位移、x_c为x方向速度，得方程（1.1）：
至于摆杆，虽然摆杆的下端固定在小车上，但摆杆的质心却是存在垂直和水平两向位移的。水平方向上，摆杆受力为支撑力的水平分量；垂直方向上，摆杆的受力包括重力和支撑力的垂直分量。
除此之外，摆杆存在转动，绕质心的转动方程为：
然而，上述动力学系统中，四个物理坐标仅仅有两个是相互独立的，
因此，在实际的数值仿真中，为了更好的与物理现象相对应，我们选取小车的横坐标x_c和摆杆的转角θ作为状态量。摆杆质心的横纵坐标与x_c及θ的关系如下：
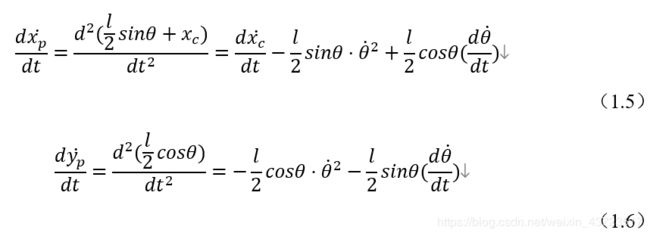小车所收到的摩擦力与运动方向相反，与相对滑轨的正压力成正比，摩擦力F_f可表示为：
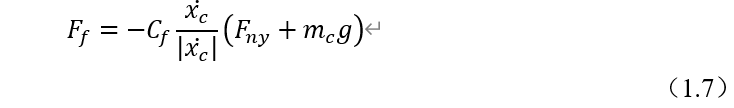联立上述方程，即可得到用于适合于数值求解的方程格式：
1.2倒立摆的数值仿真
如上，即完成了倒立摆的数值仿真建模。我们将方程在编程中实现，并调用ode45()函数，即可实现倒立摆的MatLab仿真。
[t,y]=ode45(@CartPole_Eqs,[0,T_step],OdeInput,opts);
function dotPara=CartPole_Eqs(t,Para)
global Mc Mp Lp Cf g;
X=Para(1);
V=Para(2);
Theta=Para(3);
Omega=Para(4);
Fc=Para(5);
dotPara=zeros(4,1);
dotPara(1,:)=V;
if V~=0
D1=V/abs(V);
else
D1=0; %停滞状态下不考虑摩擦力，实际上，除去初值外，dotx几乎不为0
end
C21=(Mc+Mp)/Mc+3/4*Mp/Mc*cos(Theta)*(Cf*D1*sin(Theta)-cos(Theta));
C22=Fc/Mc-(Mp+Mc)/Mc*Cf*D1*g+(sin(Theta)+cos(Theta)*Cf*D1)*Mp/Mc*Lp/2*(Omega^2)+0.75*(Cf*D1*sin(Theta)-cos(Theta))*Mp/Mc*sin(Theta)*g;
dotPara(2,:)=C22/C21;
dotPara(3,:)=Omega;
dotPara(4,:)=1.5/Lp*(sin(Theta)*g-cos(Theta)*dotPara(2));
dotPara(5,:)=0;
二、倒立摆的DQN控制
想要使用DQN控制倒立摆，有两个问题需要解决。第一，是DQN的状态和动作分别是什么？第二，DQN的奖赏如何定义？
对于第一个问题，DQN的状态就是倒立摆动力学系统的状态，包括四个参量，小车的横坐标、水平速度，摆杆的转角以及旋转角速度。对于DQN的动作，我们知道倒立摆的平衡是由控制力F_c实现的，因此其动作自然应该是控制力。但控制力本身是连续量，在依据策略选择动作时我们没办法将这一连续量的所有值都遍历一遍以获得Q值最大的控制力。因此，**我们将倒立摆的控制力离散化成一个控制力数组来实现DQN需要的动作输入，**也就是说，倒立摆的控制力输出为一组规定的常值。**在仿真模拟中，智能体每隔规定间隔进行一次状态采样，输入DQN网络中获得该状态下所有动作的Q值并选择Q值最高的动作，此控制力即为下一时间段的控制力输出。**也就是说，由于DQN的特点，我们采用幅值和时间上均离散的控制力来实现倒立摆的控制。
对于第二个问题，我们希望，倒立摆的小车水平位置距离导轨越近越好，摆杆如垂直方向的夹角越小越好。由于整个倒立摆控制程序中，需要在多个地方进行奖赏reward()的计算，我们将奖赏封装成如下的函数：
function reward=Reward_Cal(CPstate)
global X_threshold Theta_threshold;
r1=1.4*((X_threshold-abs(CPstate(1)))/X_threshold-0.8);
r2=(Theta_threshold-abs(CPstate(3)))/Theta_threshold-0.95;
reward=r1+r2;
奖赏的定义对DQN控制器的表现存在着较大的影响，r1与r2的权重决定了DQN对两种位置误差的敏感程度。也因此，奖赏的定义本身也是倒立摆DQN控制中可以调试的参数。读者也可尝试对奖赏函数进行修改来观察DQN的表现。
三、 倒立摆程序设计
我们修改在网格迷宫中搭建的MatLab程序框架，以实现其对倒立摆的控制。变化主要有以下几点：
- 由于神经网络智能体和倒立摆环境参数较多，参数的初始化单独用两个.m文件封装，这样也方便了参数的调整与检查。
- 将观察期和训练期合并成了一段代码，缩短代码长度，便于检查和维护。
- 单训练周期内，循环变量由次数变为时间，且时间的步进为可调参数。
- 在每个episode的开始，倒立摆的初始化会产生随机的扰动，一方面提高训练中的“探索”概率，另一方面模拟真实情况。
程序的框架可由下面的流程图展示。
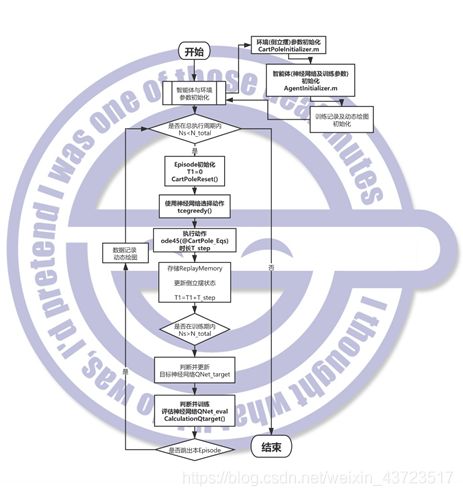程序的主体部分则如下：
% 忘记面孔的Batou
% "I thought what I'd do was I'd pretend I was one of those deaf-mutes, or should I?"
clear all;
run('CartPoleInitializer');
run('AgentInitializer');
%训练周期设置：观察期，训练期
N_obs=300;
N_train=3000;
N_total=N_obs+N_train;
T_episode=60; %每个周期的总时间
%数据记录初始化，状态记录在Episode开始前进行
TimeRecord=zeros(1,N_total);
AveTimeRecord=zeros(2,N_total/10);
ATRpointer=1;
%episode及其余设置
T_step=0.1;
n_step=1;
%动态绘图初始化
Plotset=zeros(2,1);
p = plot(Plotset(1,:),Plotset(2,:),...
'EraseMode','background','MarkerSize',5);
axis([0 N_obs+N_train 0 60]);
for Ns=1:N_total
CPstate=CartPoleReset(); %CPstate为4*1矩阵，x,dotx,theta,dottheta
T1=0;
%初始化历史记录。记录下列内容：1.控制时长；2.每个episode的600个状态与控制力矩
TrackPointer=1;
TrackRecord(Ns).Track=zeros(6,T_episode/T_step);
while T1<=T_episode
%根据tcegreedy策略选择动作
[act,Qnow]=tcegreedy(Ns,CPstate,QNet_eval);
Fc=FcTable(act);
%使用Ode45执行动作
OdeInput=[CPstate;Fc];
[t,y]=ode45(@CartPole_Eqs,[0,T_step],OdeInput,opts);
Nsize=size(y); Nsize=Nsize(1);
Newstate=y(Nsize,1:4); Newstate=Newstate';
%Replaymemory记录+指针更新
Rmemo(:,Memopointer)=[CPstate;act;Newstate];
Memopointer=PointerMove(Memopointer,S_memo);
%轨迹数据记录更新
TrackRecord(Ns).Track(:,TrackPointer)=[T1;CPstate;Fc];
TrackPointer=TrackPointer+1;
%更新状态
T1=T1+T_step;
n_step=n_step+1;
CPstate=Newstate;
%按照T-renew间隔更新估计Q_target的目标神经网络QNet_target
if (mod(n_step,N_renew)==0)&&(Ns>=N_obs)
QNet_target=QNet_eval;
end
%按照T_gap的间隔训练估计Q_eval的评估神经网络QNet_eval
if (mod(n_step,N_gap)==0)&&(Ns>=N_obs)
%1. 利用Rmemo生成训练数据级
Trainset=zeros(10,nBatch); %前9行与replaymemory一致，后一行为利用QNet_target计算得到的Q_target;
i=1;
while i<=nBatch
num1=unidrnd(S_memo);
if Rmemo(5,num1)>0 %有记录的第五行始终不为零
Trainset(1:9,i)=Rmemo(:,num1);
i=i+1;
end
end
%2. 计算Q_target
Trainset(10,:)=CalculationQtarget(Trainset(1:9,:),QNet_target);
%3. 训练QNet_eval
QNet_eval=train(QNet_eval,Trainset(1:5,:),Trainset(10,:));
end
%判断是否跳出本episode，并记录控制时长
if (abs(CPstate(1))>X_threshold)||(abs(CPstate(3))>Theta_threshold)
TimeRecord(Ns)=T1;
break;
elseif T1>=T_episode
TimeRecord(Ns)=T1;
break;
end
end
%动态绘图
if mod(Ns,10)==0
Ave1=mean(TimeRecord(Ns-9:Ns));
AveTimeRecord(:,ATRpointer)=[Ns;Ave1]';
ATRpointer=ATRpointer+1;
TempP=[Ns;Ave1];
Plotset=[Plotset,TempP];
set(p,'XData',Plotset(1,:),'YData',Plotset(2,:));
drawnow
axis([0 N_obs+N_train 0 60]);
end
end
四、Let it RUN
完成程序后，我们运行程序以观察智能体的训练。在倒立摆模型中，我们不能再简单的以智能体是否到达终点作为性能评估的标识，而以每一个episode中DQN控制倒立摆不倒（小车的坐标距离中心的偏差和摆杆的转角均不超过门限）的时长作为观察其性能的标志。我们取每10个Episode的控制时长作平均进行绘图，得到DQN的训练情况：
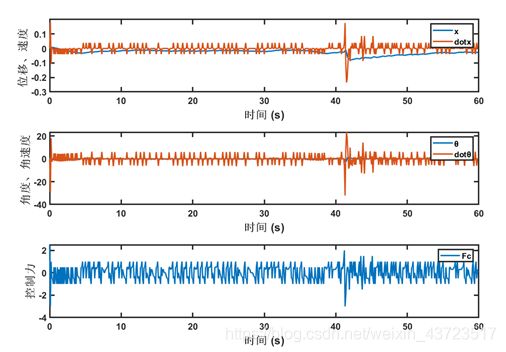
在训练完成后，单个Episode里，倒立摆呈现出如下的运动状态：
