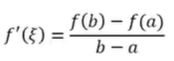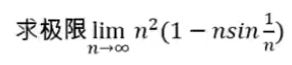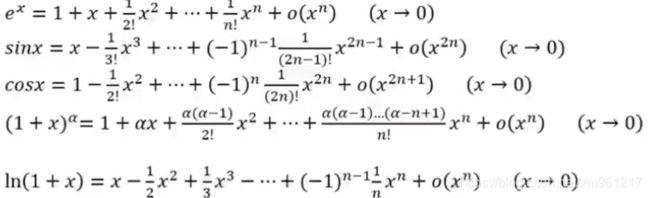数学原理-高等数学复习笔记 ——1.2 泰勒公式 罗尔中值定理与拉格朗日中值定理(附加多个实战题目)
微分中值定理
罗尔(Rolle)微分中值定理
设 f(x) 在闭区间[a,b]上连续,并且f(a)=f(b).又假设 y=f(x) 在(a,b)内可导,则必存在一点 c∈(a,b),使得 f'(c)=0
简单来说就是一个连续且可导的函数,在两个相等的端点中间必存在一条水平切线。
拉格朗日(Lagrange)微分中值定理
函数在闭区间 [a,b] 连续,开区间 (a,b) 可导,则比存在一点属于开区间内的数,使得
这个公式是什么意思呢,主要表达的意思是,在这个连续的函数上,存在某一点的斜率,诶!这个斜率啊,正好等于闭区间两端组合成一个直线的斜率,也就是两个直线平行。其实也是罗尔中值定理的进一步变换
那我们怎么证明拉格朗日中值定理呢
推论一
闭区间连续,开区间可导,f'(x)=0,则f(x) 恒等于 C,其中 C 是常数
推论二
设 f(x),g(x) 在闭区间连续,在开区间可导,f'(x) = g'(x),则 f(x) = g(x) + C
柯西(Cauchy)微分中值定理
柯西中值定理的特殊形式,g(t)=t 时,就相当于是拉格朗日中值定理。
泰勒公式
我们先讲一下泰勒公式的作用。用简单的多项式函数来表现复杂的函数,以 n 阶导无限接近原函数,也就是说通过改变系数,我们可以写出任何函数曲线,送读者们一颗心,【旺柴】方便后面能多算几道题
泰勒公式我们在另一篇文章已经有了通俗易懂的解释,想要有个总体性的认知的同学可以先看一下那一篇
数学原理-高等数学复习笔记 ——1.1 泰勒公式 泰勒展开式
上面的 Rn(x) 称为泰勒公式余项,而我们写的泰勒多项式确并不是与此相同,这就是由佩亚诺后期对泰勒公式进行进一步修改后,缩小的泰勒公式余项的范围
泰勒公式实战
理论其实很容易就理解,为了防止日后再次把泰勒公式计算过程忘记,这次我决定算一算题目,我从网上找了一道题,大家可以先看题目,计算完答案,再看我的计算过程
这里说了,麦克劳林公式,也就是说让我们在 x=0 的位置做展开(不带 ^ ,带括号,表示下标, ^ 表示上标)
也就是我们要求这个 a(k) = f^k(0)/k!
这里函数是一个指数函数 exp(x) ,也就是说多少阶都是她本身
(如果有同学有兴趣还可以看一下为什么 exp(x) 的导数等于他本身 指数函数 f(x)=exp(x) 求导后为什么还是它本身?)
a(k) = f^k(0)/k! = 1/(k!)我们每次求泰勒展开基本都是求这个公式,把每个 x 前的通项求出来即可,也就是 f^k(x)
f(x) = f(0) + (f'(0)/1!)x + (f''(0)/2!)x^2+...+(f^n(0)/n!)x^n + o(x^n)
= 1+1*x +...+x^n/n! + o(x^n) (x -> 0)
这样我们就完成了
大家可以再试着自己做做这道题
过程我就不多阐述,我把通项的值挂出来
a(k) = f^k(0)/k!
求 f^k(sin0)
f^k(sinx) = sin(x+kπ/2)
f'(0) = (sin0)' =1
f''(0) = (sin0)'' = 0
f^k(0) = sin(kπ)
为奇数次导数时 = (-1)^n k = 2n+1
为偶数的时候 = 0 k = 2n
这个可以大家自己算算看
不过也不是所有的题目都可以无脑的进行多阶求导
先做一下变形
f(x) = 1/2 - 1/2cos(x+2x^2)
= 1/2 -1/2(cos2cos(2x^2) - sin2sin(2x^2))
也就是我们只要做 cos(2x^2) 和 sin(2x^2) 的展开就好
也就是 cosx 展开的变形
也有的题目不会那么绝情,会让你求几阶就好了
第一步,常规套路,我们先尝试一下暴力求导
会发现变成了 两个未知项相乘 f'(x) = -exp(cosx) * sinx
这种越边越多的套路,除非你真的很能算,最好还是另寻方法
第二步,我们观察这个函数,复杂的地方也只有 cosx ,我们可以尝试一下换元法
但我们之前能成功换元,原因是因为我们换不换元,都是趋向于 0 的。
而这里是趋向于 1 的,那我们可以让它趋向于 0 吗?
第三步,让它趋向于 0
拆一个 e 出来即可
f(x) = e * exp(cosx-1)
....
作者算到这里的时候已经头壳隐隐作痛,希望好心的读者把剩下的步骤写出来
再留几道附加题:
为了防止读者猝死,留下几个减少脑负担的常见公式
后面的文章会讲解一下这个余项的原理与内容
以及各种导数的数学文章,(好吧我知道写反了,该先写导数)