LeetCode探索下的字节跳动面试专题全记录
前几天做完了这个专题，还是整理一下吧，感觉题目都不算很难，不过题目比较连惯，大多由简到难，简单题对稍难的题有一定的启发性。
字符串
1.无重复字符的最长子串
比较简单粗暴的想法就是没尝试添加一个字符，则回溯与前面比较，如果出现重复的，则将开始点设为重复字符位置+1，这样的时间复杂度为O（n2）.
当然还有巧妙的方法，滑动窗口，时间复杂度O(n)
借助HashMap完成，map的key为字符，value为上一次出现的索引。如果遇到存在了，则更新start为重复元素的索引+1 和 val。
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character,Integer> map = new HashMap<>();
int max = 0,start =0;
for(int i=0;i<s.length();i++){
char c= s.charAt(i);
if(map.containsKey(c)){
start = Math.max(map.get(c)+1,start);
}
map.put(s.charAt(i),i);
max = Math.max(max,i-start+1);
}
return max;
}
}
最长公共前缀
只需要遍历每个字符串的前k个字母即可，若任意字符串到达串底或者有一个匹配不上，则结束
class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs==null||strs.length==0){
return "";
}
int ans = 0;
lab:
for (int j = 0; j < strs[0].length(); j++) {
char pre = strs[0].charAt(j);
for (int i = 0; i < strs.length; i++) {
if(strs[i].length()<=j||pre!=strs[i].charAt(j)){
break lab;
}
}
ans++;
}
return strs[0].substring(0,ans);
}
}
字符串的排列
1.排列也就是说顺序无所谓 ->某个字符串一共有多少个，可预先存于一个结构中（HashMap，数组也行）
2.子串就是要求是连续的。->如果碰到非s1的字符且没有将s1字符串完全匹配完则之前匹配作废，需要重置。
这题可以使用双指针，当两个指针间距等于了s1，则匹配成功。
因为我们预先将s1的字符数量存于了一个容器中，所以遇到匹配上的减去即可，右指针向后移动，当某个字符减为负的时候，可将它恢复，直到左指针指到右指针位置或者为负的那个字符恢复为0的状态。
class Solution {
public boolean checkInclusion(String s1, String s2) {
int[] ccount = new int[256];
IntStream.range(0,s1.length()).forEach(i->ccount[s1.charAt(i)]++);
for(int left =0,right=0;right<s2.length();right++){
char c = s2.charAt(right);
ccount[c]--;
while(left<=right&&ccount[c]<0){
ccount[s2.charAt(left++)]++;
}
if(right-left+1==s1.length()){
return true;
}
}
return false;
}
}
字符串相乘
一般利用字符串相乘啊，字符串相加啊，都是使用的竖式计算的那种方式。
加法：对应位数相加，进位保留到下一位一起相加，之后有一道链表加法的与之类似，到时候再细讲吧
乘法：竖式乘法，可以将乘数拆解成，个、十、百、千…与逐个与另一个的位数相乘（1），同样将该位存于该位（2），进位到下次计算时再加上（3）。然后每一轮乘完若需要进位，则存于下一位（4）。
最后注意有可能开头会有0，也可能全为0，所以需要至少剩下一个数的情况下，去掉所有的前缀0（5）
class Solution {
public String multiply(String num1, String num2) {
int[] ans = new int[num1.length()+num2.length()];
for(int i = num1.length()-1,next = 0;i>=0;i--){
int n1 = (num1.charAt(i)-'0');
for(int j=num2.length()-1;j>=0;j--){
int n2 = num2.charAt(j)-'0';
int inx = num1.length()+num2.length()-i-j-1-1;
//（1）
int a = n1*n2;
//（2）
ans[inx] += a%10+next;
//（3）
next = a/10+ans[inx]/10;
//（2）
ans[inx] %= 10;
}
//（4）
ans[num2.length()+num1.length()-1-i] = next;
next = 0;
}
StringBuilder sb = new StringBuilder();
for(int i =ans.length-1,flag=1;i>=0;i--){
if(flag==1&&i!=0&&ans[i]==0) {
//（5）
continue;
}
sb.append(ans[i]);
flag = 0;
}
return sb.toString();
}
}
翻转字符串里的单词
按照空格分割为数组，再反向输出即可。
class Solution {
public String reverseWords(String s) {
s.trim();
String[] ss = s.split("\\s+");
StringBuilder sb = new StringBuilder();
for(int i=ss.length-1;i>=0;i--){
sb.append(ss[i]+" ");
}
return sb.toString().trim();
}
}
简化路径
…/操作主要是针对回退到前一个路径，也就是相当于…/之后的后一个路径节点删掉…/前一个路径。1
./操作相当于不变2
其他除了/…//这种类型，都是合法的文件名3
由于1，这题可以用栈结构模拟过程。
首先将字符串按照‘/’分割。
然后顺向进栈。
遇到…再弹出前一个，如果栈不为空。遇到. 和空不做处理，遇到其他将字符串存起来。
然后再以队列的方式出队，拼接"/"。
注意如果是空队列，需要补充为"/"
class Solution {
public String simplifyPath(String path) {
String[] ss = path.split("/");
Deque<String> deque = new ArrayDeque<>();
for(String s:ss){
if(s.equals("..")) {
if (!deque.isEmpty())
deque.pop();
}else if(!s.equals(".")&&!s.equals(""))
deque.push(s);
}
StringBuilder sb = new StringBuilder();
while (!deque.isEmpty()){
sb.append("/"+deque.pollLast());
}
return sb.length()==0?"/":sb.toString();
}
}
复原IP地址
这题很明显可以用回溯法
分成4段，每一段都在0～255之间，也就是1，2，3位。
而选位数又有个判断，如果选了后，至少在数字的长度上得被剩余的段数够分，而且不会多了。
也就是说假设目前是在选第x段的位数，那么剩余的数字的位数，得处于【（4-x）*3～（4-x）*1】
当然还需要使得选取的位数组成的数字位于【0，255】之间。
注意，0不能作为一个长度不为1的字符串数字的开头。
class Solution {
public List<String> restoreIpAddresses(String s) {
List<String> ans = new ArrayList<>();
if(!(s==null||s.length()<4))
store(s,new StringBuilder(),0,0,ans);
return ans;
}
private void store(String s,StringBuilder sb,int inx,int count,List<String> ans){
if(count==4){
sb.deleteCharAt(sb.length()-1);
ans.add(sb.toString());
sb.append(".");
return;
}
for(int i=0;i<3;i++){
int y = s.length()-inx-i-1;
if(y<=(3-count)*3&&y>=3-count&&judge(s,inx,i)){
sb.append(s.substring(inx,inx+i+1)+".");
store(s,sb,inx+i+1,count+1,ans);
sb.delete(sb.length()-i-2,sb.length());
}
}
}
private boolean judge(String s, int inx, int offst) {
if(inx+offst>=s.length()||(s.charAt(inx)=='0'&&offst!=0))
return false;
int num = 0;
for(int i=inx+offst,t=1;i>=inx;i--,t*=10){
num+=(s.charAt(i)-'0')*t;
}
return num<256;
}
}
数组与排序
三数之和
由于结果要为0，所以要么三个数全是0，要不然肯定存在至少一个负数/正数。那么我们就先将数组排序。使用三个指针，来指向三个数字。
1.left(指向三个数字中最小或者与2,3相等的数字，代码中用的i)：初始化指向排序后的数组开头，如若left>0了，则退出判断，输出结果。
2.right(指向最大的数字或相等)：初始化指向排序数组的末端。
3.next(指向中间大小数字，代码中用的left)：left的后一个。
然后注意对于重复元素的去重。
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.parallelSort(nums);
List<List<Integer>> list = new ArrayList<>();
for(int i=0;i<nums.length-2&&nums[i]<=0;i++){
int num1 = nums[i];
if(i>0&&num1==nums[i-1])
continue;
int left = i+1,right = nums.length-1;
while (left<right){
int sum = nums[left]+nums[right]+num1;
if(sum==0){
List<Integer> ans = new ArrayList<>();
ans.add(num1);
ans.add(nums[left]);
ans.add(nums[right]);
list.add(ans);
do {
left++;
} while (left<right&&nums[left]==nums[left-1]);
do{
right--;
}while (right>left&&nums[right]==nums[right+1]);
}else
if(sum>0){
right--;
}else {
left++;
}
}
}
return list;
}
}
岛屿的最大面积
这题可用dfs也可用bfs。我习惯用dfs，然后利用沉岛的思想。将探索过的岛屿沉没，防止重复探索。
class Solution {
public int maxAreaOfIsland(int[][] grid) {
if(grid==null||grid[0].length==0)
return 0;
int max = 0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]==1){
max = Math.max(max,dfs(grid,i,j));
}
}
}
return max;
}
private int dfs(int[][] grid, int i, int j) {
if(i<0||i>=grid.length||j<0||j>=grid[0].length||grid[i][j]==0)
return 0;
grid[i][j] = 0;
int max = 1+dfs(grid,i+1,j)+dfs(grid,i-1,j)+dfs(grid,i,j-1)+dfs(grid,i,j+1);
return max;
}
}
搜索旋转排序数组
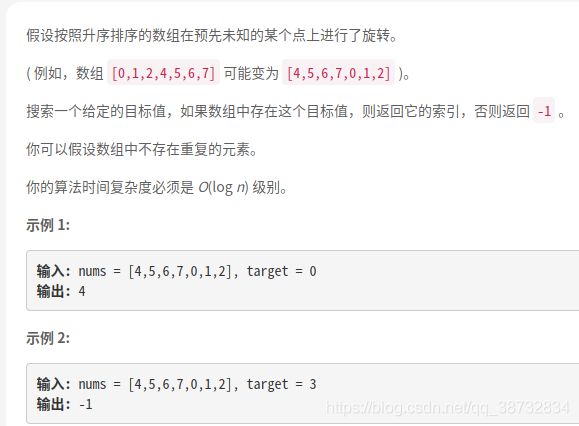
这题是剑指offer中的一题类似。（不得不说剑指offer是本挺不错的书，经典果然是经典，之前挺嫌弃它的名字的）。套用那个方法也行，找到旋转点，然后一左一右做两次二分查找。
这题肯定要利用它是排序数组旋转得到的这个特质来解决，看到排序的序列，请第一时间想到二分法。
如果是常规排序数组，查找一个数字很简单，那么这题与常规的有什么不同呢？
1.由于旋转，旋转点已左必然大于旋转点已右。
2.旋转点已左已右，自身是呈递增顺序的。
分为6种情况：
查询目标值为x，左指针为l，右指针为r，中间为mid
(1).x>len x< mid mid >len r<<
(2).x>len x>mid mid>len l>>
(3).x>len x>mid mid< 0 r <<
(4).x<0 x>mid mid<0 l>>
(5).x<0 x
终止条件就是，1.穷尽所有可能了，2.找到了。
1-> left
但是这么写有个漏洞，纯顺序就会出问题。
就需要将这些情况包括进来。
先看看这个判断与常规的逻辑，哪里有差异。
顺序 （3），（6）
x>len ,如果是顺序时，一定没有正确答案，所以可以忽略(3) 。
x<0,如果是顺序时，也没有答案，可以忽略(6).
。
再加一个顺序的判断即可。直接加一个分支感觉有点臃肿，可将(6)或者（3）条件加以限制(或者将(5)或者（2)加以拓宽）
（这题还能简略，画个卡诺图，求下最简式）
class Solution {
public int search(int[] nums, int target) {
if(nums==null||nums.length==0)
return -1;
int left = 0,right = nums.length-1;
while (left<right){
int mid = left+right>>1;
if(nums[mid]==target) {
left = mid;
break;
}
if(target>nums[nums.length-1]){
if(nums[mid]<target&&nums[mid]>nums[nums.length-1])
left = mid+1;
else
right = mid-1;
}else{
if((nums[mid]>target&&nums[mid]<nums[0])
||(nums[0]<nums[nums.length-1]&&nums[mid]>target))
right = mid-1;
else
left = mid+1;
}
}
return nums[left]==target?left:-1;
}
}
最大连续递增序列
如果一个连续的序列被中断了，则它前面的元素都可以弃置了，直接从中断处开始下轮搜索即可。
class Solution {
public int findLengthOfLCIS(int[] nums) {
if(nums.length==0){
return 0;
}
int ans =0,pre=nums[0]-1,count=0;
for(int i:nums){
if(i>pre){
count++;
}else{
ans = Math.max(count,ans);
count=1;
}
pre = i;
}
ans = Math.max(count,ans);
return ans;
}
}
数组中的第K个最大元素
四舍五入有两种做法。
1.堆
使用一个大顶堆，输出它的前k个元素即可。这里使用的是优先队列（由于优先队列是小顶堆，所以输出后K个）
class Solution {
public int findKthLargest(int[] nums, int k) {
if(nums==null||nums.length==0)
throw new RuntimeException("输入不合法");
PriorityQueue<Integer> pq = new PriorityQueue<>();
for(int i:nums){
pq.offer(i);
if(pq.size()>k)
pq.poll();
}
return pq.poll();
}
}
当然时间充分也可以自己实现一个大顶堆。详细的可看下排序中堆排序的部分，按照堆排序中类似的思想，将数组映射为一个大顶堆。
所谓大顶堆，就是父节点大于子节点的一个堆，父子索引之间的映射关系为：f = （s-1）/2.
class Solution {
public int findKthLargest(int[] nums, int k) {
int ans =0;
int count =0;
buildHeap(nums,0);
while(k-->0){
ans = nums[0];
swap(nums,0,nums.length-1-count);
adjustment(nums,0,++count);
}
return ans;
}
private void buildHeap(int[]nums,int inx){
int left = (inx<<1)+1;
int right = left+1;
if(left>=nums.length)
return;
buildHeap(nums,left);
buildHeap(nums,right);
if(nums[left]>nums[inx]){
swap(nums,left,inx);
adjustment(nums,left,0);
}
if(right<nums.length&&nums[right]>nums[inx]){
swap(nums,right,inx);
adjustment(nums,right,0);
}
}
private void adjustment(int[]nums,int inx,int offst) {
int left = (inx<<1)+1;
int right = left+1;
if(left>=nums.length-offst)
return;
if(right>=nums.length-offst||nums[left]>nums[right]){
if(nums[left]>nums[inx]) {
swap(nums, left, inx);
adjustment(nums, left, offst);
}
}else if(right<nums.length){
if(nums[right]>nums[inx]) {
swap(nums,right,inx);
adjustment(nums,right,offst);
}
}
}
private void swap(int[] nums,int inx1,int inx2){
nums[inx1]^=nums[inx2];
nums[inx2]^=nums[inx1];
nums[inx1]^=nums[inx2];
}
}
2.快速选择
可以说是快排的一半吧？我们只选择目标k在的那一边进行搜索。
假如比较后，目标值大于了分界值，则我们取右边的那一部分…小于取左边部分，相等了，输出值。
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSelect(nums,0,nums.length-1,nums.length-k);
}
private int quickSelect(int[] nums, int l, int r, int k) {
int left =l,right = r;
int num = nums[l];
while (l<r){
while (r>l&&nums[r]>=num)r--;
if(nums[r]<num)
nums[l] = nums[r];
while (l<r&&nums[l]<=num)l++;
if(nums[l]>num)
nums[r] = nums[l];
}
nums[l] = num;
if(l==k)
return num;
if(l<k){
return quickSelect(nums,l+1,right,k);
}else {
return quickSelect(nums,left,l-1,k);
}
}
}
但是这种实现效率方式极低，它与快排类似，效率完全取决于分界点的选取。
有几种选择方式，可以每次选取中间位置。
因为中间位置的要么是上一次已经确定小于某数的值，要么是大于，比较可能位于中间分界点。
class Solution {
public int findKthLargest(int[] nums, int k) {
return quickSelect(nums,0,nums.length-1,nums.length-k);
}
private int quickSelect(int[] nums, int l, int r, int k) {
if(l<r) {
int num = nums[l];
nums[l] = nums[l+r>>1];
nums[l+r>>1] = num;
int left = l, right = r;
num = nums[l];
while (l < r) {
while (r > l && nums[r] >= num) r--;
if (nums[r] < num) {
nums[l] = nums[r];
l++;
}
while (l < r && nums[l] <= num) l++;
if (nums[l] > num) {
nums[r] = nums[l];
r--;
}
}
nums[l] = num;
if (l == k)
return num;
if (l < k) {
return quickSelect(nums, l + 1, right, k);
} else {
return quickSelect(nums, left, l - 1, k);
}
}
return nums[k];
}
}
最长连续序列
两种思路，1.dp 2.贪心？
1.dp的条件就是求最优情况， 能否划分为子问题，且子问题存在最优结构，无后效性。
如果需要求一个最长的序列，那么就要使得它左右序列最长。
那么dp[i] 的含义就是如果i位置存在数字时，序列的长度。
dp[i] = 1+dp[i-1]+dp[i+1];
由于时间复杂性度要求为O(n),不可能逐一更新相邻的结构，所以只更新边界。
左边界：i-dp[i-1]
右边界：i+dp[i+1]
但是这样做有个问题，如果出现重复的数字就会将之前有它的前提下更新的边界值作为新边界值所以需要判重。
这题当然可以用数组的偏移来处理，不过还是Map会方便些，所以还是采用了Map。
class Solution {
public int longestConsecutive(int[] nums) {
HashMap<Integer,Integer> map = new HashMap<>();
int max = 0;
for(int i:nums){
if(!map.containsKey(i)) {
int r = map.getOrDefault(i + 1, 0);
int l = map.getOrDefault(i - 1, 0);
int sum = r + l + 1;
max = Math.max(max, sum);
map.put(i, sum);
map.put(i + r, sum);
map.put(i - l, sum);
}
}
return max;
}
}
2.贪心？
如果想要找到最长的序列，那么一个序列最长肯定是从它的开头开始，那么我们假设每一个点都为开头，为开头的条件就是它的值-1不存在，然后将作为开头的数逐渐递增，如果递增后的值在数组中存在，则计数递增，如果不存在则结束，判断是否需要更新最大值。
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> set = Arrays.stream(nums).boxed().collect(Collectors.toSet());
int max =0 ;
for(int i:set){
if(!set.contains(i-1)){
int count =1;
while(set.contains(i+1)){
count++;
i++;
}
max = Math.max(count,max);
}
}
return max;
}
}
第k个排列
如果不用数学解法，那就使用深搜+回溯。
从最小的数字位数开始，那么当存储了k个时结束寻找，然后输出即可。
public String getPermutation(int n, int k) {
List<String> list = new ArrayList<>();
get(k,new StringBuilder(),new boolean[n],list);
return list.get(k-1);
}
private void get(int k,StringBuilder sb,boolean[] b,List<String> li){
if(sb.length()==b.length){
li.add(sb.toString());
return;
}
for(int i=1;i<=b.length;i++){
if(!b[i-1]){
b[i-1] = true;
sb.append(i);
get(k,sb,b,li);
sb.deleteCharAt(sb.length()-1);
b[i-1] = false;
}
if(k==li.size())
return;
}
}
当然这么做会很慢，那有没有什么办法可以剪枝？
当然有啦，我们可以将字符串的数量判断前置，如果数量没达到这么多，那么就跳过，一个枝的数量是它剩余的节点的阶乘。
由于我们只有当为当前字符串时才添加进去，所以回溯都省了
class Solution {
public String getPermutation(int n, int k) {
return get(n,k,new StringBuilder(),new boolean[n]);
}
private String get(int n,int k,StringBuilder sb,boolean[] b){
if(sb.length()==b.length){
return sb.toString();
}
int count = count(n);
for(int i=1;i<=b.length;i++){
if(!b[i-1]){
if(count<k){
k-=count;
continue;
}
b[i-1] = true;
sb.append(i);
return get(n-1,k,sb,b);
}
}
return "略略略";
}
private int count(int n){
int ans = 1;
while(n-->1){
ans*=n;
}
return ans;
}
}
}
朋友圈
这题也是很明显的使用深搜+回溯
跟那个最大岛屿面积那个题类似。
找到一个一个人的朋友圈，然后再搜它朋友圈的朋友圈，然后再搜朋友圈的朋友圈的朋友圈…直到这一系列朋友圈没有新朋友了，而且将被搜索过的朋友圈，都标记一下。
class Solution {
public int findCircleNum(int[][] M) {
if(M==null||M.length==0){
return 0;
}
boolean[] inxs = new boolean[M.length];
int count=0;
for(int i=0;i<inxs.length;i++){
if(!inxs[i]) {
dfs(inxs, i, M);
count++;
}
}
return count;
}
private void dfs(boolean[] inxs,int inx,int[][] M){
inxs[inx] = true;
for(int i=0;i<inxs.length;i++){
if(M[inx][i]==1&&!inxs[i]){
dfs(inxs,i,M);
}
}
}
}
合并区间
一个区间与另一个区间的重叠的条件是前者的开头位于后者的中间，或者结束位于后者的中间。
那么共有的条件就是，前者的开头要小于后者的结束，前者的结束要大于后者的开头。
可以从前往后逐一遍历，逐后寻找可以合并的数组，找到了则更新到后面，并将前置为空(方便后续操作) ，并重新选择前置，这样是为了防止后面的合并为比较大的情况后，前面又能更新的情况。
class Solution {
public int[][] merge(int[][] intervals) {
if(intervals==null||intervals.length<2||intervals[0]==null||intervals[0].length==0)
return intervals;
int count =0;
for(int i=0;i<intervals.length-1;i++){
int min = intervals[i][0],max=intervals[i][1];
for(int j=i+1;j<intervals.length;j++){
if(min<=intervals[j][1]&&max>=intervals[j][0]){
intervals[j][0] = Math.min(min,intervals[j][0]);
intervals[j][1] = Math.max(max,intervals[j][1]);
intervals[i] = null;
count++;
break;
}
}
}
int[][] ans = new int[intervals.length-count][];
for(int i=0,inx =0;i<intervals.length;i++){
if(intervals[i]!=null){
ans[inx++] = intervals[i];
}
}
return ans;
}
}
接雨水
双指针。
有两种做法，1.滑动窗口，2.一个在首一个在尾。
1.
首先一端(l)固定于一个位置，另一个指针®向前滑动，如果h[r]
这么做前面都没问题，如果最后不是一个封闭的区域就可能漏加最后那一个窗口的雨水。
如果最后一个窗口不是封闭的话，就再在最后一个窗口的范围内，逆向再做一次这个运算。
class Solution {
public int trap(int[] height) {
if(height==null||height.length<3)
return 0;
int right =1,left = 0;
int ans = 0;
int temp =0;
for(left = 0;left<height.length&&right<height.length;){
if(height[right]<height[left]){
temp+=height[left]-height[right];
right++;
}
if(right<height.length&&height[right]>=height[left]){
ans+=temp;
temp= 0;
left = right;
right++;
}
}
if(temp!=0){
temp =0;
for(int i=height.length-1,newRight =i-1;i>left;){
if(height[newRight]<height[i]){
temp+= height[i]-height[newRight];
newRight--;
}
if(newRight>=left&&height[newRight]>=height[i]){
ans+=temp;
temp= 0;
i = newRight;
newRight--;
}
}
}
return ans;
}
}
2
这个思路更好一些，实现起来也相对优雅。
一个指向开头(l)，一个指向结尾®
如果左比右大了，
如果当前右边界的最大值大于现在的高度所指的高度，则将差值加到结果中，最后将r往中间推进。
如果右比小了，
同上，右换成左即可。
如果相等，推谁都一样，仍选一边推进。
直到两个指针相遇。
class Solution {
public int trap(int[] height) {
if(height==null||height.length<2)
return 0;
int ans =0 ,left =0,right = height.length-1,leftMax = 0,rightMax = 0;
while(left<right){
if(height[left]>height[right]){
rightMax = Math.max(height[right],rightMax);
ans += rightMax-height[right];
right--;
}else {
leftMax = Math.max(height[left],leftMax);
ans += leftMax-height[left];
left++;
}
}
return ans;
}
}
链表和树
合并两个有序链表
就是归并排序合并的过程，用两个指针分别指向两个串的开头，将较小那个保留，较小的那个指针往前挪动，下一个连接挪动后与之前较大的节点。知道某个串为空为止。
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode head = new ListNode();
ListNode helper = head;
while(l1!=null&&l2!=null){
if(l1.val>l2.val){
helper.next = l2;
l2 = l2.next;
}else {
helper.next = l1;
l1 = l1.next;
}
helper = helper.next;
}
helper.next = l2==null?l1:l2;
return head.next;
}
}
当然也可以使用迭代的写法，同理。
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode head = new ListNode();
ListNode helper = head;
while(l1!=null&&l2!=null){
if(l1.val>l2.val){
helper.next = l2;
l2 = l2.next;
}else {
helper.next = l1;
l1 = l1.next;
}
helper = helper.next;
}
helper.next = l2==null?l1:l2;
return head.next;
}
}
反转链表
1.迭代
双指针，一个指针开始指向头指针的前一个指针(pre)，另一个指向头指针(cur)，每次将cur的next指向pre，然后再将pre更新为cur，再将cur指向cur原来的next。当cur为空时输出pre即可(如果只有一个元素，就输出cur)。
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null,cur = head;
while (cur!=null){
ListNode tmp = cur.next;
cur.next = pre;
pre = cur;
cur = tmp;
}
return pre==null?cur:pre;
}
}
2.递归
首先深搜到最底，然后反向链接即可，将某个节点的下一个的下一个指向自己，然后再断开它与它下一个之间的链接，就完成了一个节点与一个链之间的反向，注意返回之前的尾节点，它是现在的头结点。
public ListNode reverseList(ListNode head) {
if(head==null||head.next==null)
return head;
ListNode li = reverseList(head.next);
head.next.next = head;
head.next = null;
return li;
}
两数相加
就是一竖式加法，与字符串加法一回事（如果链表的顺序反向就又不一样了）。每一位对齐，对应相加，如果大于10了，记录下进位的结果，下一位数再加上。不过由于俩链表的长度并不一样长，所以需要另外的空间存储结果链表。
同样可以使用递归和迭代完成
递归：
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode newHead = new ListNode();
addTwoNumbers(l1,l2,0,newHead);
return newHead.next;
}
public void addTwoNumbers(ListNode l1,ListNode l2,int next,ListNode newNode){
if(l1==null&&l2==null&&next==0)
return;
if(l1!=null){
next += l1.val;
l1 = l1.next;
}
if(l2!=null){
next += l2.val;
l2 = l2.next;
}
newNode.next = new ListNode(next%10);
addTwoNumbers(l1,l2,next/10,newNode.next);
}
}
迭代：
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode newHead = new ListNode();
ListNode helper = newHead;
int next =0;
while (l1!=null||l2!=null||next!=0){
if(l1!=null){
next += l1.val;
l1 = l1.next;
}
if(l2!=null){
next += l2.val;
l2 = l2.next;
}
helper.next = new ListNode(next%10);
helper = helper.next;
next /= 10;
}
return newHead.next;
}
}
排序链表
链表的排序与数组的排序的区别在于，多了断链和重连。
联想到前一题做的两个排序链表合并，那么可以将这题拆解成n个链表合并呀，然后n/2个链表合并，n/2/2个链表合并…这个过程就是归并排序。
具体实现就是一个快慢指针来分，因为需要定位到1/2处，所以快指针比慢指针快1个单位，当快指针到达末端时，慢指针就位于1/2位置。而且需要取左中位数(取右边时在元素仅有2个时会出现死循环，一直定位到右边那个点，无法拆分)，所以一开始快指针比慢指针领先一位。
然后再以慢指针最后的位置(左中位)的下一个作为右边的开始，开头作为左边的开始，再断开这两条链。
当拆分到一定程度时(比如1个或者0个节点时无需比较直接返回)，这时会回溯到左右各一个的情况，利用之前的合并算法合并，直到整条链表合并完成。
class Solution {
public ListNode sortList(ListNode head) {
if(head==null||head.next==null)
return head;
//1.拆分
ListNode slow = head,fast = head;
while(fast!=null&&fast.next!=null){
slow = slow.next;
fast = fast.next.next;
}
ListNode nextStart = slow.next;
slow.next = null;
ListNode leftS = sortList(head);
ListNode rightS = sortList(nextStart);
//2.治+合并
return mergeTwoLists(leftS,rightS);
}
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode head = new ListNode();
ListNode helper = head;
while(l1!=null&&l2!=null){
if(l1.val>l2.val){
helper.next = l2;
l2 = l2.next;
}else {
helper.next = l1;
l1 = l1.next;
}
helper = helper.next;
}
helper.next = l2==null?l1:l2;
return head.next;
}
}
环形链表 II
如果存在环，那么使用快慢指针，肯定能够相遇。因为都在一个圈里转悠。
而这道题是定位起点，直觉告诉俺，肯定与相遇位置有关，如果相遇了，那么快指针比慢指针恰好多走了一圈。而快指针比慢指针多走了一倍的路程，那就说明到达环开启的位置(x)+慢指针在圈内走的路程(inx) = 一圈（y） ，就是说剩下的半圈就是x的长度。
1.递归：
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode target = cycle(head,head,false);
if(target==null)
return null;
int count = 0;
while(head!=target){
head = head.next;
target = target.next;
count++;
}
return head;
}
private ListNode cycle(ListNode fast,ListNode slow,boolean flag){
if(fast==null||fast.next==null||slow==null){
return null;
}
if(flag&&fast==slow){
return fast;
}
flag =true;
return cycle(fast.next.next,slow.next,flag);
}
}
2.迭代
class Solution{
public ListNode detectCycle(ListNode head) {
ListNode slow=head,fast = head;
while(fast!=null&&fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if (fast==slow){
while(head!=slow){
head = head.next;
slow = slow.next;
}
return slow;
}
}
return null;
}
}
相交链表
如果俩链表从某个点开始相交了，它们后面的链表都会是相同的节点，利用这个条件，这题就能解了，由于两条链表可能不一样长，所以选择将链表分别入各自的栈，如果找到记录下当前相交点，直到最后两边出栈元素不相等时，输出记录的最后一个相交的节点。
class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Deque<ListNode> sa = new ArrayDeque<>();
Deque<ListNode> sb = new ArrayDeque<>();
while (headA!=null){
sa.push(headA);
headA = headA.next;
}
while (headB!=null){
sb.push(headB);
headB = headB.next;
}
ListNode ans = null;
while (!sa.isEmpty()&&!sb.isEmpty()){
if((headA=sa.pop())==(headB=sb.pop()))
ans = headA;
else
break;
}
return ans;
}
}
细看题目才发现没注意到要求O(1)的内存条件。
那么只能顺序遍历，可是长短链怎么解决呢？
顺序遍历，
如果两条链等长，它们会同时遍历完，如果遇到相同的第一个节点则可以返回答案了，如果没有相交，则会在最终遇到null，也可以交了。
那么长短链的情况，短链遍历到末尾，长链就还差的距离就是与短链之间的差值，那么怎么样才能使得长短链构造成一样的长度呢？如果我们知道长短链前面的差值，让长链先走差值才让短链开始，问题就回到等长链上了。
在第一次遍历后，可以让原短链的引用变成长链开始走，直到原长链走完，这时原长链变为短链，就达成了我们的要求了。
class Solution{
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode a = headA,b =headB;
while (a!=b){
if(a==null){
a = headB;
}else {
a = a.next;
}
if(b==null){
b = headA;
}else {
b = b.next;
}
}
return a;
}
}
合并k个排序链表
前面排序俩都会做了，合并k个还不简单，憨一点的方法就是合并n-1次(如果那几个小链表所属的位置在比较靠后，就会遍历很长的那个长链表)，要不然就两两合并，大家的长度都相对类似了。就类似归并排序的并的过程。
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if(lists==null||lists.length==0){
return null;
}
return div(lists,0,lists.length-1);
}
public ListNode div(ListNode[] listNodes,int left,int right){
if(left==right)
return listNodes[left];
int mid = left+right>>1;
return mergeTwoLists(div(listNodes,left,mid),div(listNodes,mid+1,right));
}
ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode head = new ListNode();
ListNode helper = head;
while(l1!=null&&l2!=null){
if(l1.val>l2.val){
helper.next = l2;
l2 = l2.next;
}else {
helper.next = l1;
l1 = l1.next;
}
helper = helper.next;
}
helper.next = l2==null?l1:l2;
return head.next;
}
}
二叉树的最近公共祖先
两个节点在最近的祖先之前的路径都是一样的，是不是有点像之前那道相交的链表那道题反过来。
可以先找到一个节点后，回溯上一个节点，搜索另外个方向，看能否找到，如果找到了，返回一个标志位，直接跳出所有的栈，没找到，则进入下一个选择。
如果这些都找不到说明另一个节点是之前找到那个节点的子节点。也就是说当我们第一个两个方向都找到的节点就是根节点，如果一直回溯完都找不到，先找到的那个节点一定是另一个节点的子节点。
static class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null||root==p||root==q)
return root;
TreeNode l = lowestCommonAncestor(root.left,p,q);
TreeNode r = lowestCommonAncestor(root.right,p,q);
if(l==null)
return r;
if(r==null)
return l;
return root;
}
}
这题还有一种思路，当找到第一个节点时的路径和第二个节点时的路径第一个出现分歧时，之前那个节点就是公共父节点。
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Stack<TreeNode> sk1 = new Stack<>();
Stack<TreeNode> sk2 = new Stack<>();
dfs(root,p,sk1);
dfs(root,q,sk2);
TreeNode pre = null;
while(!sk1.isEmpty()&&!sk2.isEmpty()){
TreeNode t1 = sk1.pop();
TreeNode t2 = sk2.pop();
if(t1!=t2){
break;
}else{
pre = t1;
}
}
return pre;
}
private boolean dfs(TreeNode t1,TreeNode target,Stack<TreeNode> sk){
if(t1==null){
return false;
}
if(t1==target){
sk.push(t1);
return true;
}
boolean flag = dfs(t1.left,target,sk);
if(!flag) flag = dfs(t1.right,target,sk);
if(flag) sk.push(t1);
return flag;
}
}
我使用的是用俩栈分别存储两边的路径，遇到不同的的节点时，就返回上一个节点。不过时间效率有点难顶。
看了题解，官方给出了使用哈希表，存储整棵树的父节点，然后根据目标节点的父节点，父节点的父节点…（有点连通图的味道）,回溯到树顶，将路径存入一个set中，然后另一个节点，按照同样的方式，找到第一个存在于目标set中的节点即为公共的爹。
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Map<Integer,TreeNode> fathers = new HashMap<>();
dfs(root,fathers);
Set<TreeNode> treeNodes = new HashSet<>();
while (p!=null){
treeNodes.add(p);
p = fathers.get(p.val);
}
while (!treeNodes.contains(q)){
q = fathers.get(q.val);
}
return q==null?root:q;
}
private void dfs(TreeNode root,Map<Integer,TreeNode> map){
if(root!=null) {
if (root.left != null) {
map.put(root.left.val,root);
dfs(root.left,map);
}
if(root.right!=null){
map.put(root.right.val,root);
dfs(root.right,map);
}
}
}
}
二叉树锯齿形层次遍历
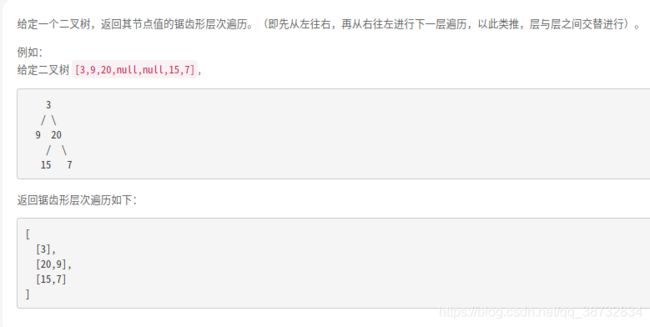这个跟层次遍历没啥区别，普通层次遍历就是读取到对应的层数时，将节点顺序存入，锯齿形就是一些随着奇偶的不同，顺序不同而已，比如此题,设为1～n层就是奇数尾插，偶数头插。
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
if(root==null)
return list;
dfs(root,list,1);
return list;
}
private void dfs(TreeNode root, List<List<Integer>> list, int level){
if(root==null){
return;
}
if(list.size()<level)
list.add(new ArrayList<>());
if((level&1)==1)
list.get(level-1).add(root.val);
else
list.get(level-1).add(0,root.val);
dfs(root.left,list,level+1);
dfs(root.right,list,level+1);
}
动态规划和贪心
买卖股票的最佳时机
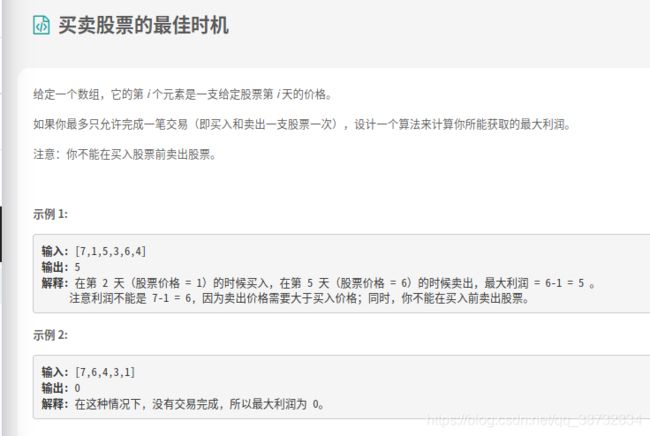这题之前做过一个系列的股票，有个套路，每天初始都只有两种状态。
持有：无操作->持有，卖出->不持有
不持有:买入->持有 ，无操作->不持有
就是两种状态对应的两种操作。只需要记录下每天对应的四种情况，即可最后知道最大值。
一个状态来记录当前是否持有，一个状态来记录当前的操作，还有一个状态来设置允许的操作次数。
状态定义：
dp[n][k][i]:第n天第k次交易时，原始状态为i(非持有即不持有)。
转移方程：
dp[n][k][持有]= max(dp[n-1][k][不持有]-当日价，dp[n-1][k][持有])。
dp[n][k][不持有] = ，max(dp[n-1][k][不持有]，dp[n-1][k-1][持有]+当日价格)。
初始化：
dp[0][0][持有] = -当日价格
压缩状态：
由于天数都是昨天的，可以将天数压缩。反着更新就可以直接覆盖
由于本题只能进行一次操作，所以不存在上一次交易后的情况，我们可以将买入次数限定为1.
也就是不加之前的累加值。
class Solution {
public int maxProfit(int[] prices) {
if(prices==null||prices.length<2)
return 0;
int[] dp = new int[2];
//持有
dp[1] = -prices[0];
for(int i=1;i<prices.length;i++){
dp[1] = Math.max(dp[1],-prices[i]);
dp[0] = Math.max(dp[0],dp[1]+prices[i]);
}
return dp[0];
}
}
买卖股票的最佳时机2
与上题同理，由于可以无限制买卖，所以加上之前的收益即可
class Solution {
public int maxProfit(int[] prices) {
if(prices==null||prices.length<2)
return 0;
int[] dp = new int[2];
//持有
dp[1] = -prices[0];
for(int i=1;i<prices.length;i++){
dp[1] = Math.max(dp[1],dp[0]-prices[i]);
dp[0] = Math.max(dp[0],dp[1]+prices[i]);
}
return dp[0];
}
}
干脆把全部股票再捋遍吧。如果交易数为2时应该如何处理呢？
一个交易的开始是从购买开始，卖出结束。
那么第一次交易应该从买入开始，我们第二次交易的开始只能从第一次交易的结束开始。（逆向更新防止覆盖）
class Solution {
public int maxProfit(int[] prices) {
if(prices==null||prices.length<2)
return 0;
int[][] dp = new int[2][2];
//持有
dp[0][1] = Integer.MIN_VALUE;
dp[1][1] = Integer.MIN_VALUE;
for(int i=0;i<prices.length;i++){
dp[1][1] = Math.max(dp[1][1],dp[0][0]-prices[i]);
dp[1][0] = Math.max(dp[1][1]+prices[i],dp[1][0]);
dp[0][1] = Math.max(dp[0][1],-prices[i]);
dp[0][0] = Math.max(dp[0][0],dp[0][1]+prices[i]);
}
return dp[1][0];
}
}
然后如果k设定为某个不确定的值呢？注意如果k的大小超出天数的一半，可认为可以无限次交易.还需要注意的是，0次交易额为0.
class Solution {
public int maxProfit(int k,int[] prices) {
if(prices==null||prices.length<2||k==0)
return 0;
if(k>=(prices.length>>1))
return maxProfit(prices);
int[][] dp = new int[k][2];
Arrays.stream(dp).forEach(n->n[1]=Integer.MIN_VALUE);
for(int i:prices){
for(int j=k-1;j>=01;j--){
dp[j][0] = Math.max(dp[j][0],dp[j][1]+i);
dp[j][1] = Math.max(dp[j-1][0]-i,dp[j][1]);
}
dp[0][0] = Math.max(dp[0][0],dp[0][1]+i);
dp[0][1] = Math.max(dp[0][1],-i);
}
return dp[k-1][0];
}
public int maxProfit(int[] prices) {
int have = Integer.MIN_VALUE,noHave = 0;
for(int i:prices){
have = Math.max(have,noHave-i);
noHave = Math.max(noHave,have+i);
}
return noHave;
}
}
那如果一次交易后含为期一天的冷冻期无法立即开始下次交易呢？
解决方式也很简单，多保存前一天的交易就行了。
class Solution {
public int maxProfit(int[] prices) {
int preNoHave =0,have = Integer.MIN_VALUE,noHave = 0;
for(int i:prices){
int tmp = noHave;
noHave = Math.max(noHave,have+i);
have = Math.max(have,preNoHave-i);
preNoHave = tmp;
}
return noHave;
}
}
含手续费
class Solution {
public int maxProfit(int[] prices, int fee) {
int have = -prices[0],no = 0;
for(int i=0;i<prices.length;i++){
have = Math.max(have,no-prices[i]);
no = Math.max(no,have+prices[i]-fee);
}
return no;
}
}
最大正方形
如果需要找到一大的个正方形，nn的，那么在(n-1,n)位置，肯定可以构成一个(n-1)(n-1)的正方形。在(n-1,n-1)还有(n,n-1)也是。
那么只需要找这三个方向上最小的正方形+1即为当前最大正方形。
状态定义：
dp[i][j] :(0～i,0～j)位置最大面积。
转移方程：
dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
初始化：
为了避免循环里面判断耗时，将边界位置，预先设定，为1的地方设为1.
class Solution {
public int maximalSquare(char[][] matrix) {
if(matrix==null||matrix.length==0||matrix[0].length==0)
return 0;
int max = 0;
int[][] dp = new int[matrix.length][matrix[0].length];
for(int i=0;i<matrix.length;i++) {
dp[i][0] = matrix[i][0] - '0';
max = Math.max(dp[i][0],max);
}
for(int i=0;i<matrix[0].length;i++) {
dp[0][i] = matrix[0][i] - '0';
max = Math.max(dp[0][i],max);
}
for(int i=1;i<matrix.length;i++){
for(int j=1;j<matrix[0].length;j++){
if(matrix[i][j]=='1') {
int t = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j-1]);
dp[i][j] = t + 1;
max = Math.max(dp[i][j],max);
}
}
}
return max*max;
}
}
最大子序和
这题严格来说算是贪心，只要加上结果加上下一个数字比单纯的下一个数字大，就保留，如果没有，则只选下一个数字。
class Solution {
public int maxSubArray(int[] nums) {
int max = Integer.MIN_VALUE,sum =0;
for(int i:nums){
sum = Math.max(i,sum+i);
max = Math.max(sum,max);
}
return max;
}
}
三角形最小路径和
计数dp的一种类型。
从顶端走道低端，每次都有两个选择路径，或者说每个位置有两种来源（除了左边界和右边界）。那么就选最小的那个来源即可。
话说这是接触的第一道动态规划题就是这种类型，比这题还简单，当时是一个矩形，想想自己还是进步挺多的。
三角形第i(1~n)层长度是i。
利用这个特性，我们可以将dp数组的长度定为n。数组的定义很直接就是某个位置时最小的和。
考虑到由于边界值的来源只有一个，所以我们在边界的外面加一个最大值。减少不必要的判断。
想象一下将图中那个三角形左对齐，可以发现。dp[i][j] = min(dp[i-1][j],dp[i-1][j-1])+该点处的值。
也就是说某个位置值仅与上一层的头顶上和它前一个有关。
为了实现O(n)的额外空间，所以我们反着更新。
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
if(triangle==null||triangle.size()==0)
return 0;
int[] dp = new int[triangle.size()+2];
dp[0] = Integer.MAX_VALUE;
for(int i=0;i<triangle.size();i++){
List<Integer> tmp = triangle.get(i);
for(int j=i;j>=0;j--){
dp[j+1] = Math.min(dp[j],dp[j+1])+tmp.get(j);
}
dp[i+2] = Integer.MAX_VALUE;
}
return Arrays.stream(dp).min().getAsInt();
}
}
俄罗斯套娃信封问题
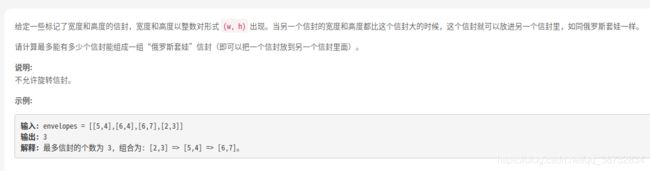打败套娃的方式是套娃哈哈哈哈哈哈。
这题就是最大上升序列的二维版，那么我们只需要将一维排序（顺序，当然求逆序也可以对应的求最大下降序列），另一维按最大上升序列找就行了呗。然后注意排序维相等时，逆序，因为信封一样大是无法放下的，而且不允许旋转。
求上升序列是一个线性dp问题。
想要找到一个当前点最长的上升序列，肯定需要寻找上一个小于当前值的最长的那个序列。
class Solution {
public int maxEnvelopes(int[][] envelopes) {
if(envelopes==null||envelopes.length==0)
return 0;
Arrays.sort(envelopes,(o1,o2)->{
if(o1[0]==o2[0])
return o2[1]-o1[1];
return o1[0]-o2[0];
});
int max =1;
int[] dp = new int[envelopes.length];
Arrays.fill(dp,1);
for(int i=1;i<envelopes.length;i++){
for(int j=i-1;j>=0;j--){
if(envelopes[i][1]>envelopes[j][1])
dp[i] = Math.max(dp[i],1+dp[j]);
}
max = Math.max(max,dp[i]);
}
return max;
}
}
既然 是最大上升序列，当然有个优化方式啦，利用二分法，是基于这样的假设，要想某个序列尽可能长，那么到同样的长度的数字就要尽可能的小。如果一个数字与前面的数字能形成长度为3的序列，而另一个数字也能，而后者小于前者，当我们有一个数字大于后者时，则它至少可以形成一个长度为4的序列。
在如此的假设下的dp数组必然是一个单调递增的序列，我们就可以使用二分查找了。
class Solution {
public int maxEnvelopes(int[][] envelopes) {
if(envelopes==null||envelopes.length==0)
return 0;
Arrays.sort(envelopes,(o1,o2)->{
if(o1[0]==o2[0])
return o2[1]-o1[1];
return o1[0]-o2[0];
});
int max = 0;
int[] dp = new int[envelopes.length];
dp[0] = envelopes[0][1];
for(int[] i:envelopes){
int tmp = i[1];
if(tmp>dp[max]){
dp[++max] = tmp;
}else {
int left = 0, right = max;
while (left < right) {
int mid = left + right >> 1;
if (dp[mid] <tmp)
left = mid+1;
else
right = mid;
}
if (tmp < dp[left])
dp[left] = tmp;
}
}
return max+1;
}
}
数据结构
最小栈
最小栈，就是需需要获取某个值为栈顶时的最小值，那么可以将最小值绑定到节点上，这样添加时只需读取一下前者的最小值即可。如果自身比它小，则将与自己绑定的最小值更新为自己否则不变。这样就实现了O(1)时间复杂性度下获取该值。
class MinStack {
private int size;
private Node head;
private static class Node{
int val;
Node next;
int min;
Node pre;
Node(){}
Node(int val,int min){this.val = val;this.min = min;}
}
/** initialize your data structure here. */
public MinStack() {
}
public boolean isEmpty(){
return size==0;
}
public int size(){
return size;
}
public void push(int x) {
if(isEmpty()){
head = new Node(x,x);
}else{
head.next = new Node(x,Math.min(x,head.min));
head.next.pre = head;
head = head.next;
}
size++;
}
public void pop() {
if(isEmpty()){
throw new RuntimeException("栈为空");
}
Node temp = head.pre;
if(temp!=null)
head.pre.next = null;
head.pre =null;
head = temp;
size--;
}
public int top() {
if(isEmpty()){
throw new RuntimeException("栈为空");
}
return head.val;
}
public int getMin() {
if(isEmpty()){
throw new RuntimeException("栈为空");
}
return head.min;
}
}
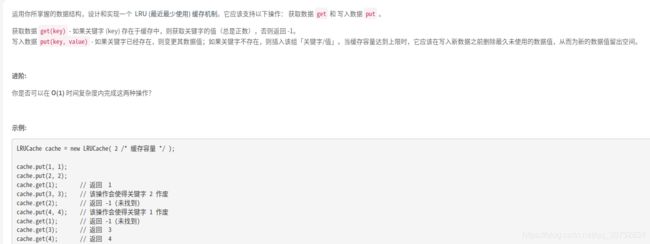
LRU缓存机制
俺在之前为了讲LinkedHashMap时候做过详细题解
全是O(1)的数据结构
我用的思路与上一题类似的思路，使用了一个双向链表穿着map，使节点的大小从小到大排列。顶端为最小值，末端为最大值。
Inc:要么不存在，直接插入到头节点，值为1，如果存在，则将它递增，探索到与它原来值一样大的最后一个节点，将该节点置于它之后。
Dec:如果不存在，不处理，如果存在，则减1，并向前查找与它原值一样大的第一个值，将该节点移动到该位置即可。
Inc和Dec虽然方向相反，但是整体的操作逻辑是一样的，先短链，取出目标节点，重连断开位置(如果是首尾节点需要更新)，然后寻找到合适的位置，将目标节点插入然后增大/减小1，如果变为头尾节点，需要更新。
头尾节点的特征就是头没有前节点，尾没有后节点。
public class AllOne{
private Map<String ,Node> map;
private static class Node{
Node pre;
Node next;
int val;
String key;
public Node(String key,int val) {
this.val = val;
this.key = key;
}
}
Node head,tail;
private void addNode(Node nv) {
//添加于头，空链,非空链
if(head==null){
tail =nv;
}else {
head.pre = nv;
nv.next = head;
}
head =nv;
}
private void setNode(Node nv,int val) {
Node temp = nv;
nv.val+=val;
Node tmp = null;
//1 往后找，到第一个大于等于递增后相同的数字，调整到它的next，
// -1，往前找，同理
if(val==1){
if(tail!=nv){
while (temp.next != null && temp.next.val < nv.val){
temp = temp.next;
tmp = temp;
}
if(tmp!=null){
//1.将原位置断开重连
removeNode(nv);
//2.将nv插入新位置
nv.pre = tmp;
nv.next = tmp.next;
if(tmp.next!=null){
tmp.next.pre = nv;
}else{
tail = nv;
}
tmp.next = nv;
}
}
}else{
if(head!=nv){
while (temp.pre != null && temp.pre.val > nv.val){
temp = temp.pre;
tmp = temp.pre;
}
if(tmp!=null){
//1.将原位置断开重连
removeNode(nv);
//2.将nv插入新位置
nv.next = tmp;
nv.pre = tmp.pre;
if(tmp.pre!=null){
tmp.pre.next = nv;
}else{
head = nv;
}
tmp.pre = nv;
}
}
}
}
private void removeNode(Node nv) {
//Node位于中，位于首，位于尾
Node p = nv.pre,n = nv.next;
if(p!=null){
p.next = n;
}else {
head = n;
}
if(n!=null){
n.pre = p;
}else {
tail = p;
}
}
/** Initialize your data structure here. */
public AllOne() {
map = new HashMap<>();
}
/** Inserts a new key with value 1. Or increments an existing key by 1. */
public void inc(String key) {
if(key==null){
throw new RuntimeException("key不能为null");
}
Node nv = map.get(key);
if(nv==null){
nv = new Node(key,1);
map.put(key,nv);
addNode(nv);
}else{
setNode(nv,1);
}
}
/** Decrements an existing key by 1. If Key's value is 1, remove it from the data structure. */
public void dec(String key) {
if(key==null){
throw new RuntimeException("key不能为null");
}
Node nv;
if((nv=map.get(key))!=null){
if(nv.val ==1){
map.remove(key);
removeNode(nv);
}
setNode(nv,-1);
}
}
/** Returns one of the keys with maximal value. */
public String getMaxKey() {
return tail==null?"":tail.key;
}
/** Returns one of the keys with Minimal value. */
public String getMinKey() {
return head==null?"":head.key;
}
}
拓展练习
前俩题有种CF里前一两道题的感觉。
x的平方根
如果不用数学方法，那么就只能遍历1～x/2的范围内是否为有满足条件的值，1～x/2这意味着啥？顺序呀，二分查找嘛
class Solution {
public int mySqrt(int x) {
if(x<2)
return x;
int left = 1,right = x>>1;
while(left<right){
int mid = left+right>>1;
long ans = (long)mid*mid;
if(ans < (long)x){
left = mid+1;
}else {
right = mid;
}
}
if((long)left*left>(long)x){
return left-1;
}else {
return left;
}
}
}
UTF-8 编码验证
这题的意思就是说。
如果最高位数字为0，合法。如果有高位开始有n个连续的1的，就需要后面就需要接n-1个最高位为1，次高位肯定不为1的数字(高位连续的1只有1个)，高位仅1位为1的数字不能单独出现。
顺序遍历数字即可，每个数字的范围都是0~255.
统计某个数字的高位有几个1，记录下来，遇到1个高位仅1个连续为1的就减去，如果减完了则将下一个数字的高位1来更新连续1的个数(不能为1).
如果没减完，则没有高位仅1个连续1的不合法。
如果当前需要减的为0了，单独出现高位仅1个连续1的不合法。
最后再输出有没有将前面的1的位数减干净即可。
class Solution {
public boolean validUtf8(int[] data) {
int num = 0;
for(int i:data){
int count = pre(i);
if(num!=0&&count==1){
num--;
}else if(num==0&&count<5&&count!=1){
num =Math.max(count-1,0);
}else {
return false;
}
}
return num==0;
}
private int pre(int num) {
int count =0;
for(int i=0;i<8;i++){
if((num&1)==1){
count++;
}else {
count=0;
}
num>>=1;
}
return count;
}
}
第二高的薪水
这是一道SQL题
查询第二高的，还得不重复，可以根据Salary分组去重，然后排序输出第二个即可。当然有可能不存在，全员一个工资，那么我们就需要使用一个叫做IFNULL的函数，如果不存在，则返回NULL。
如果Salary上建立得有索引，且为覆盖索引，GROUP BY可能会比DISTANIN快，而DISTANIN是全表扫描。
SELECT IFNULL((SELECT salary FROM Employee
GROUP BY 1 ORDER BY 1 DESC LIMIT 1,1),NULL) AS SecondHighestSalary;
当然可以用子查询查出最大值，然后去掉它，再查找一次最大值。
SELECT Max(Salary) AS SecondHighestSalary FROM Employee WHERE Salary NOT IN (SELECT Max(Salary) FROM Employee);