在上一篇文章里我们简单的讲述了下什么是理财以及理财对我们的意义,在这一篇文章中我们将会对理财的渠道进行一些比较,从而得出属于我们自己的理财观点.
现在我们继续使用我们常用的toy modle来进行推理:
假设现在有两个点A,B他们的风险是一样的,但是他们的投资回报是不一样的(假设这个风险是严格风险,考虑到所有意外情况的发生,比如跑路等等),那么如果风险一样的话大家会选择哪个进行投资,显而易见会是B.因为B的回报率会更高,这是我们首先关心的,接着我们会关心说如果两个回报率相同的点,但是他们的风险可能是不一样的,这时候我们一定会选择A,因为我们A相对于C会更加的稳定,但是我们为什么会这样选择?
首先,风险不是说以一定的概率会亏损或者失去这些回报,或者是有一定的概率去获得这样的超额的回报,因为这里的我们期望的收益E是他的期望,而不是他的上限,所以这件事情并不是这么的显然,这里我们需要一个简单的证明,我们在这里补充一下;
1:为什么人是风险厌恶的?
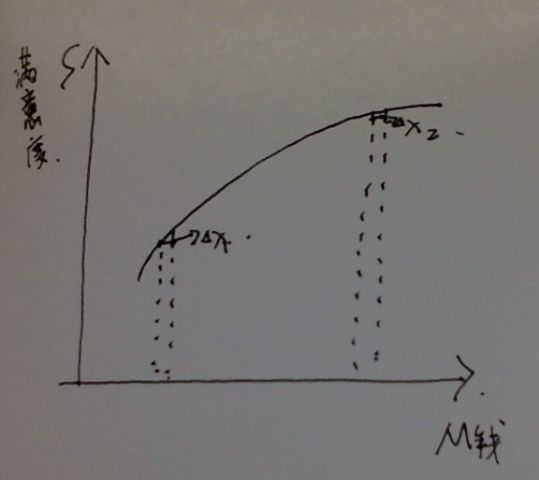
说起风险的衡量,我们首先要说一下我们是拿什么东西来衡量的我们愿不愿意进行投资或者是一种配比,其实说到底,最后最后还是归结于我们开不开心,我们做一个偏好的选择,其实是做一种满意度的比较,而且这个满意度的比较每个人可能是不一样的,有不同的曲线,比如可能对于我来说,我可能有10万块的总资产的时候满意度就非常高,但是对于另外一个人来说可能满意度就非常低,所以说这个满意度的曲线是有历史依赖的,但是无论如何在任何一个时刻,一个人的满意度曲线是根据他的资产的变多而变大,这个是可以接受的(所以他的斜率是正的),并且这个斜率是不断降低的,降低意味着我特别没钱的时候,我多一个单位的钱我就会比较开心(类似于边际效益递减),
如果大家认为他的斜率为正并且随着金钱数量的增加满意度斜率会不断降低这件事是无可辩驳的话,那么我们就来分析一下,在这种情况下他是投资厌恶的?无论他此刻现在资产是多少:
假设现在某一个人的资产是M0,那么说风险我们通常理解的是在某一种资产的情况下,可能会有偏移,简单的来说,现在可能一个人有50%的概率资产减少1000元,以50%的概率增加1000元,那么我们可能现在就说他的风险可能是1000元,这是一个简单的描述,因为真实的情况要用偏移的概率分布来讲的,但是简化来说就是这样.那这时候假设他的风险更大,比如说有50%的概率有3000元的震荡,这个时候就会有另外的一种情况,这个时候我们结合他的函数图像,我们就可以发现更多有趣的东西:
如果现在震荡点为A点,那么如果他的风险震荡是1000的话,那么他有可能会变成B的满意度,或者是B’的满意度,各以1/2的概率出现,如果风险更大的话,它是以C或者C’一点出现,那么这个时候如果不确定的话,其实他的平均的满意度应该是这两个点的一个平均,因为这个曲线是上突的,那么B和B’的中值满意度就是这个图中的所示,但是C和C’点的中值满意度是低于B和B’的点的,因为这个函数是这样的,我们就可以简单的证明.
因此无论现在任何一个人资产是多少,如果只给你风险而没有给你收益的话,你是会拒绝的,所以说风险偏好这件事情我们能够感受到,但是实际上也是有一些东西在支撑的,一旦我们接受人的满意度是斜率大于0并且不断降低的话,那么我们就能够得到A点的这个投资渠道是优于C点的,因为他们的期望值是一样的,并且凭空而来的风险我们是厌恶的,那么这样就得到了一个非常重要的结论.
那么这时候就会有人说为什么会有人去额外的承担风险(现实生活中有这样的例子),其实这样一种是额外的风险往往会承诺额外的收益的,比如我们去做一个P2P理财,他拿一个很大的收益来吸引我们,我们可能会愿意承担风险,即使这个平台有可能跑路,即使我们身边不靠谱的同学推荐给我们的,我们也有可能会相信,因为他的投资收益可能会更大,还有一种情况是(我自己也想不通,但是实际上会发生的情况),有一些人是愿意去赌博的,并且他也知道可能带来的期望是负的,因为赌场总是赚钱的,(赌场其实是靠大数定律最终怎么能够去收敛,或者是有隐瞒赌局的某一种手段来赚钱的),所以一个赌徒,如果他要去赌场的话,平均来说他应该是要亏钱的,但是还是有人去做,这也就是有一部分人他对风险其实并不是那么的厌恶,他甚至会主动地去承担风险,他可能会主动地去丢一个钢镚,比如丢到正面赚100元,丢掉反面亏102元,是有人愿意去丢的,但是我们认为这样的人就是不是那么理性,但是我们想一想我们认识的,我们总会遇得到这样的人,但是我们所讨论的不是这样的一小部分人,我们讨论的是大部分的人,以及我们之后讨论的基金经理的行为,基金经理其实没有什么好说的,他一定是经受过这样的考验的,别人才会放心的给他钱,所以我们都按照上边的情况来进行分析,我们认为受到良好教育的人的世界观里面,B投资是优于A投资的,A投资是优于C投资的.
那有趣的事情来了,我们知道投资的种类是非常多的,如果我们简单的进行投资的渠道比较的话我们是可以比较的,但是我们要面临的问题远远不是画一个不等号的问题,而是我应该有多少钱投到什么地方.这才是我们真正关心的,你要具体告诉我百分50投什么,剩下的百分50再去投什么,这才是我需要的答案,这时候我们就需要先想一个问题,如果我们明显的知道有A,B,C三个投资,他有明显的优劣,并且有不等式的传递性的话,在这样的一个简单的情况下,我们是应该做简单的单一投资还是应该做多元投资.
首先这时候我们先建设投资的渠道有两个A和A’,这个A的收益小风险小,A’风险大收益高,这么来看,这两个没有明显的优劣,但是在这样没有明显优劣的情况下,是会分散投资的,但是如果有明显优劣的情况下,我们会怎么选择.肯定是选优的,就跟刚才的那个B,C点,C点的收益低并且风险高,但是B点风险低还收益高,我们肯定会去投资B,但是这个结论是错误的,我们现在来证明为什么这是一个错误的结论,即使B点明显优于C点,我们也应该分散投资.
因为几乎多元投资几乎永远是正确的,下面我们来证明这个匪夷所思的结论,而这个结论是很有意义的,因为他可以作为我们将来理财的主导思想,下面我们来证明这件事情,证明证明这件事情也是很有意思的:
首先证明的话,我们首先要介绍一个无差别曲线:
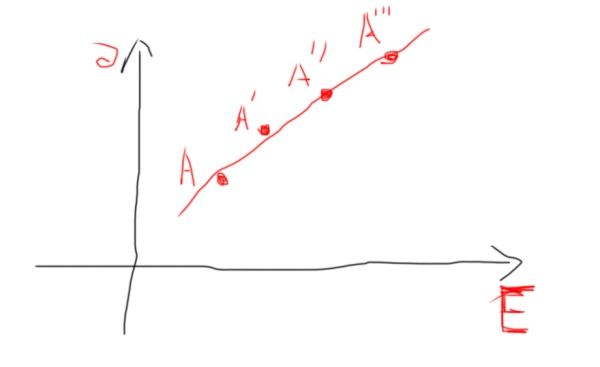
因为我们要去分散投资或者是单一投资,我们都需要去比较一下投资渠道的好坏,在上边我们说了,A和A’,这两个可能是很难比较的,因为对不同的人,是有不同的偏好的,因为对于有的人我可以冒很大的风险,但是有的人还是觉得这是一个可控的风险,但是对于单一个人和投资体来说,他有个人的投资偏好,因此在这里我们要先去确定投资个体,其实我就可以很明显的告诉你,A对于我来说是多么的好,但是如果再让我再去承受多一点的风险,我会明确的告诉你,多给我多少收益我会接受,最后以至于A点和A’点的满意程度是一样的,对于一个具体的个人是这样的,我们自己总有一个风险接受度,并且我们总会告诉自己,你要拿多少的额外收益来抵偿我们额外的风险,这样的话我们就能画出一系列的点,而这个点练成的线我们就称为无差别曲线:
就是没有任何的差异(满意度相同),但是你换成新的个体,这个斜率就不一样,以至于你可以画出一条曲线,一般来说是曲线,你换另外一个点,你会画出一系列的无差别线,这个有点类似于等高,等压线,而对于一个具体的投资者,他就会有具体一系列的满意度(在他可以投资的二维平面里),而这时候如果有明显优劣的两个投资同时存在的话,我们是否以混搭的比例去配置一部分资产?
下一篇文章,我们一起来探索这个有趣的问题