LeetCode排序数组(插入排序(直接、希尔)、选择排序(直接、堆)、交换排序(冒泡、快排)、归并排序、基数排序)
排序
- 插入排序
- 直接插入排序
- 希尔排序
- 选择排序
- 直接选择排序
- 堆排序
- 交换排序
- 冒泡排序
- 快速排序
- 归并排序
- 基数排列
class Solution {
public int[] sortArray(int[] nums) {
Arrays.parallelSort(nums);
return nums;
}
}
hhhhh
那正好整理一下排序算法。
| 类型 | 算法名 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 插入排序 | 直接插入 | O(n2) | O(1) | 稳定 |
| 插入排序 | 希尔排序 | O(n1.3)~O(n2) | O(1) | 不稳定 |
| 选择排序 | 直接选择排序 | O(2) | O(1) | 不稳定 |
| 选择排序 | 堆排序 | O(nlogn) | O(1) | 不稳定 |
| 交换排序 | 冒泡排序 | O(n2) | O(1) | 稳定 |
| 交换排序 | 快速排序 | O(nlogn) | O(logn)~O(n) | 不稳定 |
| 归并排序 | 归并排序 | O(nlogn) | O(n) | 稳定 |
| 基数排序 | 基数排序 | O(d*(n+r))//d位数,r基数,n比较的数目 | O(n+r) | 稳定 |
插入排序
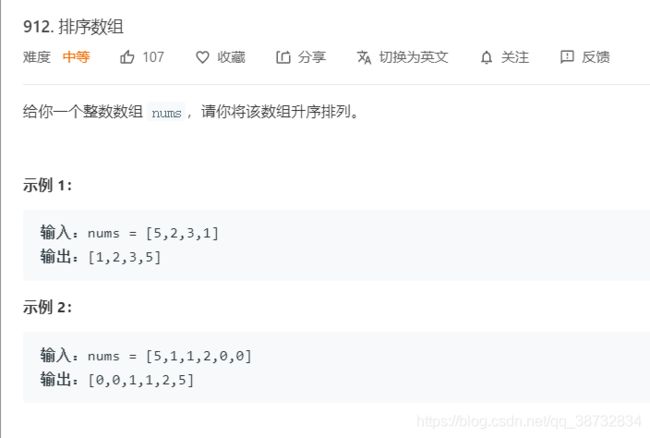
直接插入排序
思想: 如果假设前i个都是顺序排列的,第i+1个数字就应该插入到它合适的位置上,直到最后个数字都插入到合适的位置上。
算法:
- 只有一个数字的序列,肯定是顺序排列的。
- nums[i]
- 若小于,交换后,再与前面比较,直到将原来的nums[i]放到合适的位置为止。
//LeetCode居然过了
public int[] sortArray(int[] nums) {
for(int i=1;i<nums.length;i++){
for(int j=i-1;j>=0;j--){
if(nums[j+1]>nums[j]){
break;
}
else{
int temp = nums[j+1];
nums[j+1] = nums[j];
nums[j] = temp;
}
}
}
return nums;
}
希尔排序
希尔排序是直接插入排序的优化版本,首先思考一下直接插入排序在什么情况下比较有效,是不是序列基本有序或者小序列会比较高效。那么希尔排序要做的就是首先让序列基本有序。
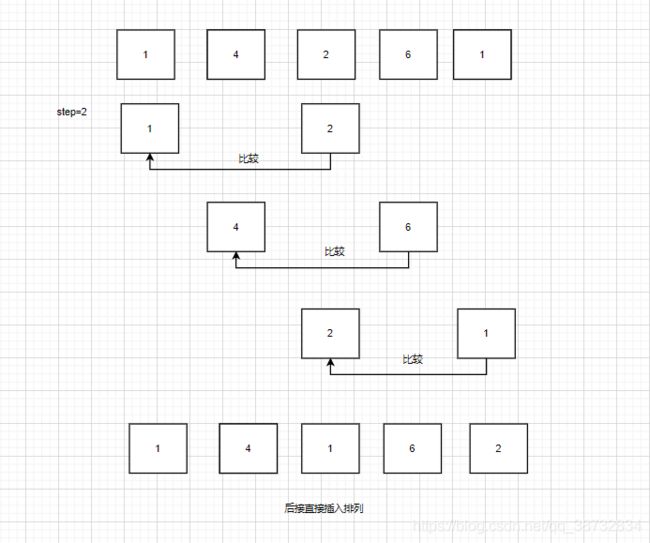
思想: 先让大范围有序,再逐渐缩小范围有序,最后回归到直接插入的形式。
算法:
1.确定初始分组大小
4. 以分组大小作为步长进行插入排序
5. 缩小分组步长进行插入排序直至缩小到步长为1.
public int[] sortArray(int[] nums) {
int h =1,size = nums.length,s = 3;
//在LeetCode里数据规模下,以3作为分割效果最好
//这个具体选择应该根据数据的形式决定,满足一个条件即为最优,
//较大h的排序的结果对最终结果尽量有益。
while((size/=s)>0){
h = h*s+1;//选择步长
}
while(h>0){
for(int i=h;i<nums.length;i++){
for(int j=i-h;j>=0;j-=h){
if(nums[j+h]>nums[j]){
break;
}
else{
int temp = nums[j+h];
nums[j+h] = nums[j];
nums[j] = temp;
}
}
}
h/=s;
}
return nums;
}
选择排序
直接选择排序
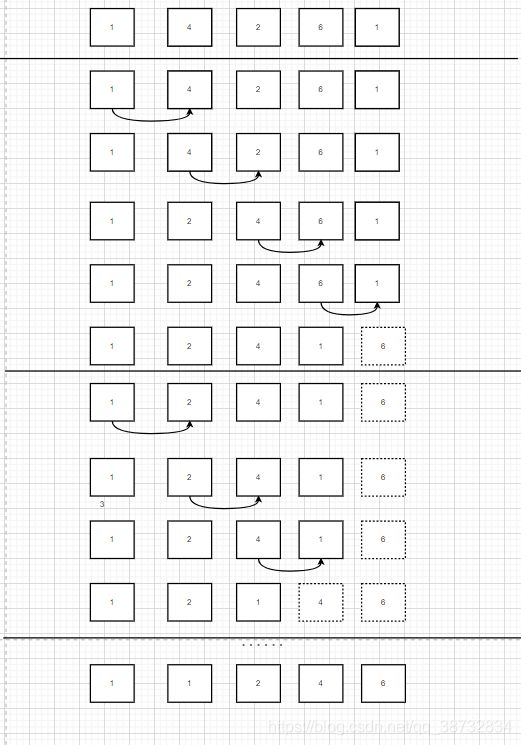
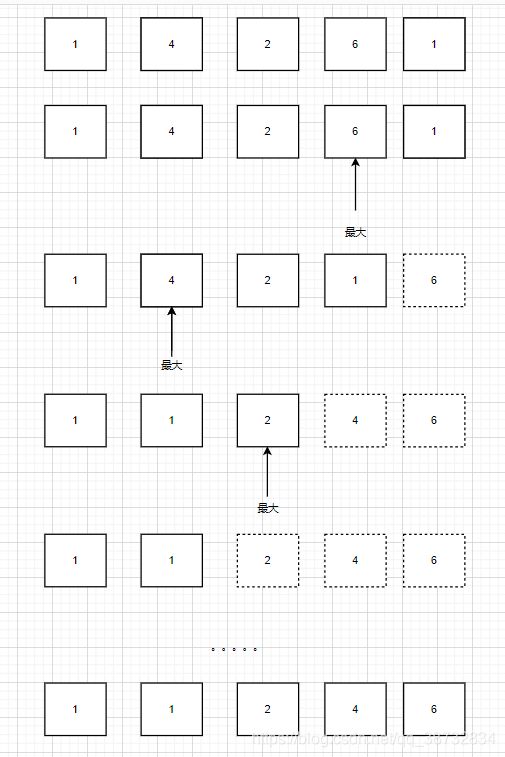
思想: 找出第i大的数字放在倒数第i的位置,直到最后,自然排序完毕。
算法:
6. 遍历0~n-1位置找出最大值与n-1位置的数字交换
7. 遍历0~n-2位置…
8. 直到遍历到0~0位置.
public int[] sortArray(int[] nums) {
for(int i=nums.length-1;i>0;i--){
int max_inx = i;
for(int j=i-1;j>=0;j--){
max_inx = nums[j]>nums[max_inx]?j:max_inx;
}
int temp = nums[i];
nums[i] = nums[max_inx];
nums[max_inx] = temp;
}
return nums;
}
堆排序
可以见得直接选择排序无论情况如何,时间复杂度都是O(n2),挺糟糕的,堆排序是它的一种优化策略,构造一个大顶堆,所谓大顶堆就是满足父节点大于子节点的二叉树 (还有一个小顶堆,就是父节点小于字节点的二叉树,升序用大顶,降序用小顶)。
思想: 构造一个大顶堆后,将最上面的结点挪到叶子结点上(就是数组的尾部),再调整大顶堆,重复上述操作,直到挪完全部结点。时间复杂度都是O(nlogn)
算法:
- 构造大顶堆,将数组索引映射为堆,调整其父子结点的大小顺序使得父节点的值必比子节点大。
- 将堆的顶点 (数组0的位置的值) 置于最后个叶子结点的位置,调整堆,缩小堆的范围
- 重复上述步骤直至堆中仅有一个数。
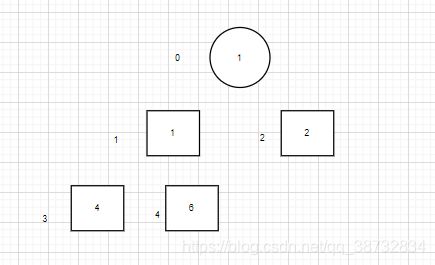
原数组:
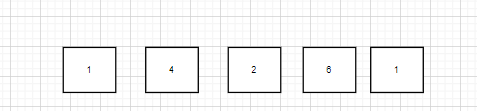
映射为堆:
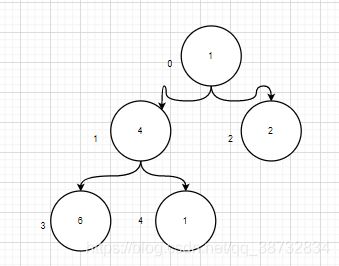
调整为大顶堆,从第一个非叶子结点 (nums.length/2-1) 开始.
父子结点的索引关系为:inx_father = (inx_son+1)/2-1
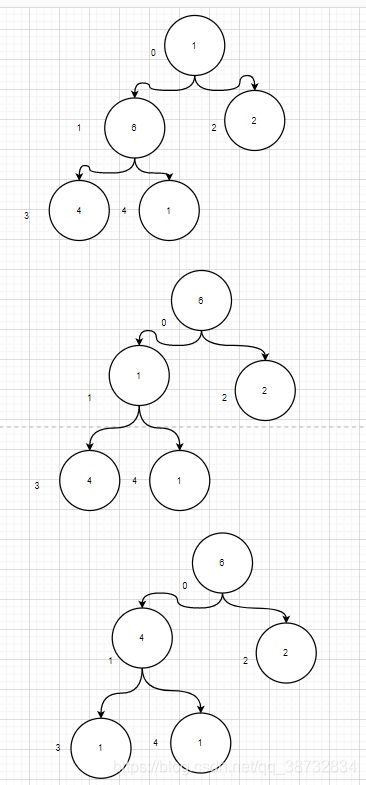
获取最大值:

重复上述步骤,直到只有叶子结点
public int[] sortArray(int[] nums) {
for(int i=nums.length/2-1;i>=0;i--){//构造大顶堆
int f = adjustHeapPart(nums,i,nums.length);
//若被调整则需要再次对应子树
while(f!=-1){
f = adjustHeapPart(nums,f,nums.length);
}
}
for(int i=0;i<nums.length-1;i++){
swap(nums,nums.length-1-i,0);
int f = adjustHeapPart(nums,0,nums.length-i-1);
//若被调整则需要再次对应子树
while(f!=-1){
f = adjustHeapPart(nums,f,nums.length-i-1);
}
}
return nums;
}
private int adjustHeapPart(
int[] nums,int father,int size){//局部调整
int son_left = (father+1)*2-1,
son_right = (father+1)*2;
int big_inx = (son_left<size?
nums[son_left]:Integer.MIN_VALUE)>
(son_right<size?
nums[son_right]:Integer.MIN_VALUE)?
son_left:son_right;//找出较大的那个子结点的索引
if(big_inx<size&&nums[father]<nums[big_inx]){
swap(nums,big_inx,father);
return big_inx;
}
return -1;
}
private void swap(int[] nums,int inx_x,int inx_y){
int temp = nums[inx_x];
nums[inx_x] = nums[inx_y];
nums[inx_y] = temp;
}
如果数据量足够大的情况下,多叉堆排序会更快。
交换排序
冒泡排序
俺学的第一个排序算法就是这个…
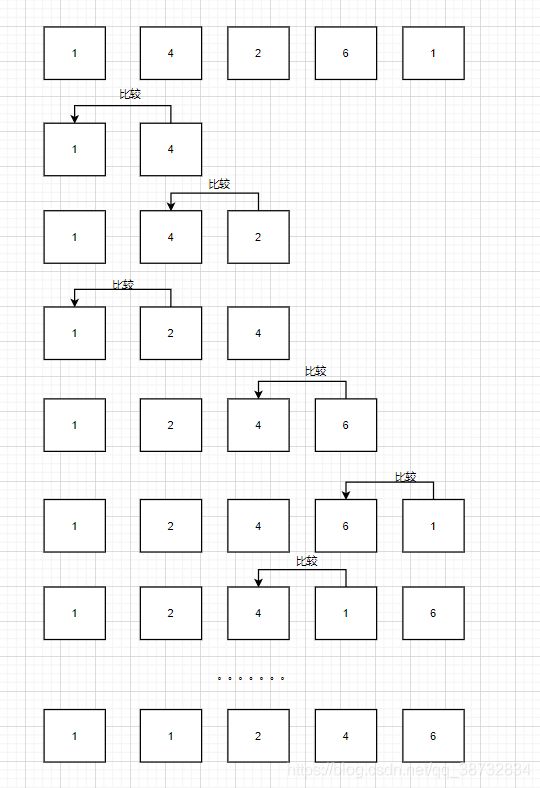
思想: 像鱼吐泡泡一样,每次都和近邻的数字进行比较,如果前大于后则交换,这样必然将泡泡冒到边界,自然就是最大的泡泡嘛,重复以往不断缩小边界,直到边界大小为1.
算法:
public int[] sortArray(int[] nums) {
for(int i=0;i<nums.length;i++){
for(int j=0;j<nums.length-i-1;j++){
if(nums[j]>nums[j+1]){
swap(nums,j,j+1);
}
}
}
return nums;
}
快速排序
啊终于到了大家都喜欢的快排。
思想: 快排有一种化整为零的思想,将比某基准数小的数字都放在基准数的左边,比基准数大的都放在基准数右边,然后再以左右两边划分子数组的分别再找个基准数,重复这种操作,直到子数组的大小为1.
算法:
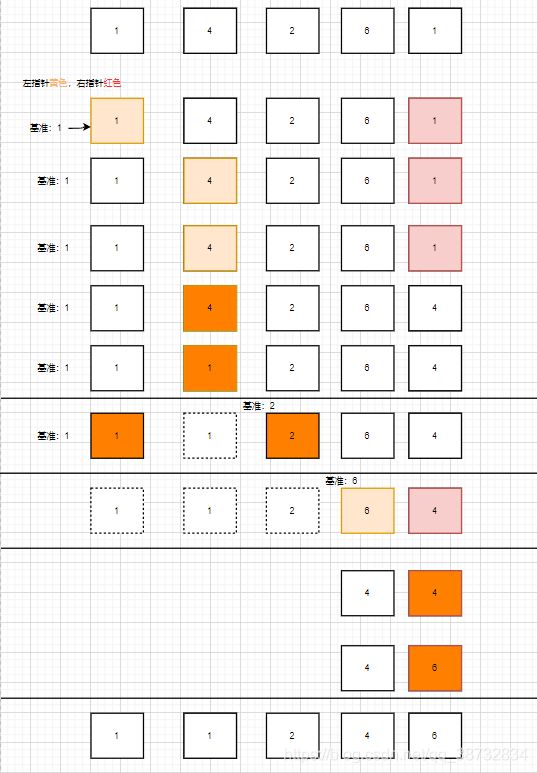
- 设定某数为基准数(以左1为基准),再创建两个指针,分别指向基准数,和数组边界位置的数字。
- 右指针开始往回找小于基准数的数字,若找到了则将右指针数字覆盖左指针数字(这时右指针那里的数字是重复的)
- 左指针往前找大于基准数的数字,若找到则将左指针所指数字覆盖右指针所指数字(这时左指针那里的数字是重复的)
- 直到两个指针相遇,这时所指的数字必然是重复的,或者就是基准数,这时将基准数覆盖他俩所指的位置。
- 这时变为了基准数已左的数字和基准数已右的数字,再将他俩重复上述操作,直到子数组长度为1.
public int[] sortArray(int[] nums) {
quick(nums,0,nums.length-1);
return nums;
}
private void quick(int[] nums,int left,int right){
if(left>=right){
return;
}
int mid = partQuick(nums,left,right);
quick(nums,left,mid-1);//左排
quick(nums,mid+1,right);//右排
}
private int partQuick(int[] nums,int start,int end){
int temp = nums[start];
while(start<end){
while(start<end&&nums[end]>temp){
end--;
}
nums[start] = nums[end];
while(start<end&&nums[start]<=temp){
start++;
}
nums[end] = nums[start];
}
nums[start] = temp;
return start;
}
在LeetCode的数据情景下,快排果然是目前为止排序最快的算法。
归并排序
这是目前一个需要自己开临时空间的排列算法。
思想:分而治之。分:将一个数组不断分割成原来的一半,直到子数组长度为1时,再合并为长度的两倍(1->2)治:将子数组直接比较排序,再合并直到复原为原数组长度。
算法:
- 将数组看成一个一个长度为1的数组
- 合并成长度为i*2的数组,比较排序,用两个指针指着需要合并的俩数组的开始位置,若左指针比右指针小,则将左指针所指的数放入零时数组中,反之亦然,直到将俩数组的值全部放入临时数组中,然后再用临时数组覆盖俩数组的位置。
- 重复2直到数组长度为原长度。
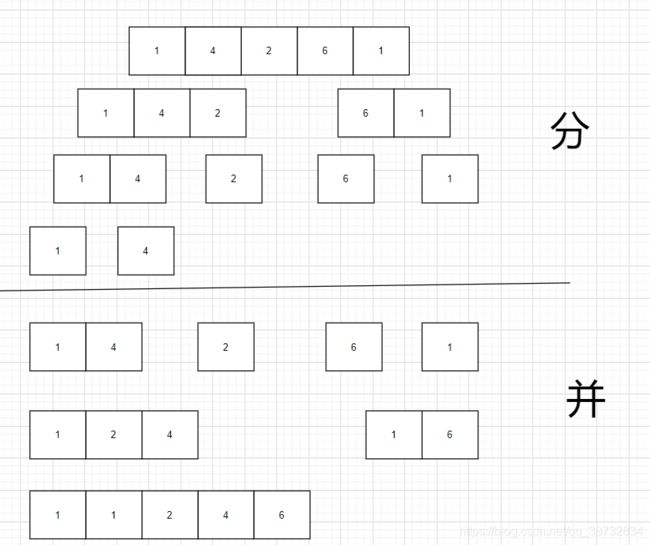
以最后次合并为例讲讲如何排序:

private void merge(int[] nums,int start,int end){
if(start==end){
return;
}
int mid = (start+end)/2;
merge(nums,start,mid);
merge(nums,mid+1,end);
partSort(nums,start,mid,mid+1,end);
}
private void partSort(int[] nums,int num1_start,int
num1_end,int num2_start,int num2_end){
int[] temp = new int[num2_end-num2_start+
1+num1_end-num1_start+1];//长度为两个子数组长度之和
int count =0;
int left= num1_start,right = num2_start;
while(left<=num1_end||right<=num2_end){
if(right>num2_end||
(left<=num1_end&&nums[left]<nums[right])){
temp[count++] = nums[left++];
}else{
temp[count++] = nums[right++];
}
}
count = num1_start;
for(int i:temp){
nums[count++] = i;
}
}
基数排列
这种排列方式与其他的排列方式都不太相同,其他排列方式核心都再与比较如果更好的比较。而这种就是收集与查找(我第一次学桶排序时感觉有点散列表的味道2333)。
思想: 将数组按照其位数不断入桶,再从低到高读取出来,再入桶,入桶的顺序自然基于前一位排列的顺序,直到所有的数子都在一个桶里取出,排序完毕。
算法:
- 先按i位存储(个,十,百…位之类)
- 从低往高遍历。
- i = i+1位 重复上述操作,直到所有的数字都存储于一个桶为止
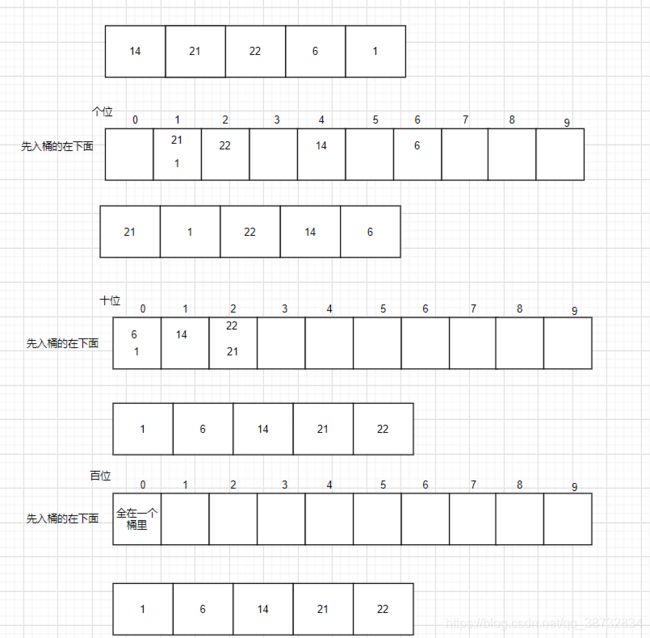
注意:这里的代码,仅支持正整数,若想支持负整数可以将桶扩容为19,再按-9 ~ 0 ~ 9的顺序存放即可。
public int[] sortArray(int[] nums) {
int count = 1;
boolean flag;
do{
flag = false;
int pre=0;
List<Integer>[] barrel = new ArrayList[10];
for(int i=0;i<nums.length;i++){
int temp = (nums[i]/count)%10;
if(barrel[temp]==null){
barrel[temp] = new ArrayList<>();
}
barrel[temp].add(nums[i]);
if(i!=0&&pre != temp){
flag =true;
}
pre = temp;
}
count *= 10;
int inx =0;
for(List<Integer> li:barrel){
if(li==null){
continue;
}
for(int i:li){
nums[inx++] = i;
}
}
}while(flag);
return nums;
}