后缀数组-SA\height详解
综述
最近在做字符串的相关工作。现阶段主要学习的是后缀数组。相比较后缀树,后缀数组的性能略差但是由于编写方便。在信息学竞赛中,性价比很高。
本篇文章主要介绍SA和height数组的求解方法。由于时间原因,一步一步介绍。
网上关于SA的介绍很多,而且非常好懂。但是对于height数组的介绍不是很到位了。所以,本次首先介绍height数组的求法。
编译器
sublime
介绍
实现目标
a) 对任意给定的字符串S,建立其后缀数组;
b) 查找一个字符串S是否包含子串T;
c) 统计S中出现T的位置和次数;
d) 找出S中最长的重复子串。所谓重复子串是指出现了两次以上的子串。
基础知识
首先说明:对于一个长度为len的字符串,后缀总共有:len个。
例如:aba,len=3。他的后缀有:aba,ba,a;三个。
SA(后缀数组)的求法
讲解
·后缀数组SA的求法:
注意SA[i] = x是指排名第i名的是x。
采用基数排序+倍增算法。一个长度为n的字符串一共有n个后缀,例如:abcd的后缀:abcd,bcd,cd,d共计4个。我们希望将字符串的后缀们按照字典序排序。如果强行快排的话,考虑到“字符串比较”的特点我们的复杂度为O(n^2logn)。这显然是不行的。所以后缀数组采用了以下办法:
首先将字符进行基数排序。(我是按照字符的ascii 码)来做的桶的。

然后两两一组再次进行基数排序。注意右侧首位如果没有那么就补0.(如下图中最右边的“2”)。
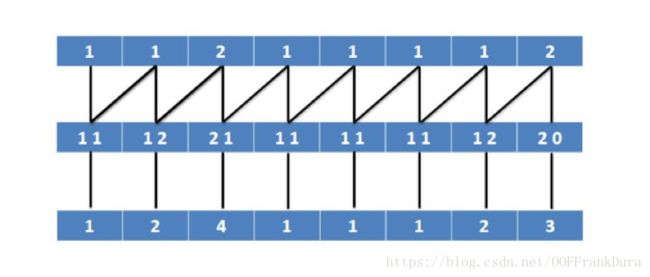
以此类推,下一次就是四四一组。注意这里的四四一组是四个字符。等到任意字符的名次都不同了,就不必进行下去了。
这里巧妙的算法思想:我们每次倍增都很好的利用了上次排序的成果。也就是说我们的第二关键字其实是该位置右侧的名次。而这个名次在上一轮就已经求出来了。所以我们只需要微做调整,就可以快速的完成第二关键的排序。然后再进行复杂度为O(n)的第二关键字的排序。这一方面得益于倍增算法的特点另一方面也得益于基数排序的特点!
注意到对于一个长度为n的字符串,我们得到了n个后缀。又注意到倍增算法的特点。我们总共需要进行logn次上述操作(上述操作是O(n)复杂度)。所以总的复杂度是O(nlogn)。可见效率提升了很多!
大概可以看一发大神关于SA的讲解
传送门:后缀数组SA求解
再简略的说一下,大概的思路是:借助于倍增的思想,我们每次进行基数排序O(len)。总共进行log(len)次。总的复杂度是:O((len)log(len))之所以需要基数排序,是因为我们通过这个排序可以将“相似”的后缀们聚集在一起/。
注意SA[i] = x代表排名第i名的是第x个后缀。
同时我们还求得了rank数组。
注意rank[x] = i代表第x个后缀的排名是i。
单纯利用SA可以进行模式匹配了。
求解SA的代码(参考):
#include 0;
for(i=0; i//以字符的ascii码为下标
for(i=1; i1];
for(i=n-1; i>=0; i--) sa[--Ws[x[i]]]=i;
/*cout<<"SA"<
for(j=1,p=1; p2 ,m=p)
{
for(p=0,i=n-j; ifor(i=0; iif(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; ifor(i=0; i0;
for(i=0; ifor(i=1; i1];
for(i=n-1; i>=0; i--) sa[--Ws[wv[i]]]=y[i];
for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1; i1],sa[i],j)?p-1:p++;
}
return;
}
int main()
{
while(scanf("%s",str)!=EOF)
{
cout << str << endl;
int len=strlen(str);
get_SA(str,sa,len+1,130);
for (int i = 1; i <= len; ++i)
cout << sa[i] << endl;
break;
}
return 0;
} height的求法
好,我们现在已经拿到了SA(后缀数组),而且我们也拿到了rank[i]。
但是只有SA和rank我们几乎啥都干不了。
我们需要建立一个数据结构:height数组。
关于height数组的证明
强烈建议,牢记sa[i]与rank[i]的对应关系并且拿出纸笔进行推导记录!
我们需要引入一个新的结构:height数组。此外还要引入系列概念:最长公共前缀lcp(注意区分lcs:最长公共子序列)。
·lcp定义:最长公共前缀的长度。通俗地说就是对于任意的两个字符串s,p从头依次比较,如果相同则继续比较。总共相同字符的最大位置。
例如:s=jkui与p=jkhh的lcp (s,p) = 2.
·LCP定义:注意区分lcp,这里的LCP服务于我们的后缀数组SA。LCP(i,j) = lcp(suffix(SA[i]),suffix(SA[j]))。通俗地讲,就是排名为i名和排名第j名的后缀的最长公共前缀的长度。
·LCP的性质:
LCP(i,j) = LCP(j,i);结合我们的定义,可知这是显然的。 (1)
LCP(i,i) = len(suffix(SA[i])) (2)
性质二也是显然的,其实就是自己和自己的lcp的值就是该串的长度。
公式(1)(2)涵盖了i大于j,i小于j,i等于j所有的情况。
如果强行计算LCP(i,j)复杂度是O(n)。显然是不可接受的。
注意还有一条性质三。
若i小于j, LCP(i,j) = min{LCP(k-1,k),i+1<=k<=j} (3)
通俗的来讲就是排名i和j之间的LCP是由区间[i,j]中两两相邻的LCP最小值决定的.这本质是由于基数排序的结果,因为整个区间是有序的。
* ·height数组定义:*
定义一维数组:height[i] = LCP(i-1,i);规定height[1] = 0.
此时再看LCP性质三:LCP(i,j)其实就是height[i],i+1小于等于k小于等于j的最小值。也即height在i+1到j之间的最小值。
结合上述分析,我们注意到:
能够解决问题4的其实就是要求最大的LCP。而经过我们的变换,我们将其转化为相邻的LCP的最大值问题。而通过定义height数组我们只需求解最大的height 值即可!
求解height我们可以利用性质:
定义 h[i] = height[rank[i]](或者height[i]=h[sa[i]])其中rank[i] = p是指在i位置的后缀的排名是p。
重要性质:对于i>1且rank[i] >1 有
h[i] > h[i-1]-1;
证明:
假设lcp(suffix(i),suffix(j))>1
首先如果suffix(i) 小于 suffix(j)那么suffix(i+1) 小于 suffix(j+1) (先后保持不变性)这是很自然的。因为我们的排序是基数排序。当两者都截去首位后按照基数排序的性质。它们仍然满足先后顺序。同时根据该分析,我们知道lcp(suffix(i+1),suffix(j+1)) = lcp(suffix(i),suffix(j))-1.
(截去特性)当h[i-1] 小于等于 1的时候(也即相邻没有公共前缀或者说只有一个的时候)。结论一定成立。因为此时h[i-1]-1小于等于0,而我们知道跟我们的定义对于任意的x都有h[x]>=0所以h[i] >= h[i-1]-1也自然成立。
当h[i-1] >1 的时候,即按照h数组定义有height[rank[i-1]]>1,因为按照height数组的定义,height[1]=0所以rank[i-1]一定是比1大的。所以rank[i-1]>1.
设j = i-1,k = SA[rank[i-1]-1]=SA[rank[j]-1]。所以即k是i-1在sa中的前一名。所以一定过suffix(k) 小于 suffix(j).又因为:
h[i-1] = lcp(suffix(k),suffix(j))>1;suffix(k)小于suffix(j)(作为前提利用截去特性)。
那么有lcp(suffix(k+1),suffix(i)) = h[i-1]-1.注意这里的suffix(k+1)和suffix(i)的排名就未必是紧邻的了!
此外我们知道rank[k+1] 小于 rank[i](也即先后保持不变性)
所以rank[k+1] 小于等于 rank[i]-1的。因为rank数组中是整数。
所以
LCP(rank[i]-1,rank[i])>=LCP(rank[k+1],rank[i]);
//注意rank[i]-1和rank[i]在排名上是紧邻的。而rank[k+1]与rank[i]保持了次序但是未必紧邻。
LCP(rank[i]-1,rank[i])>=LCP(rank[k+1],rank[i])
=lcp(suffix(k+1),suffix(i)) 这是LCP的定义。
= h[i-1]-1;利用上述绿色部分。
而LCP(rank[i]-1,rank[i]) = h[i]。
所以得证。
拿到了该性质我们可以快速计算height数组。
1.如果rank[i]==1那么h[i] = 0;(即height[1] = 0)
2.如果i==1或者h[i-1]小于等于1利用suffix(i)与suffix(rank[i]-1)前缀更新h[i].比较了h[i]+1次。
3.其他情况,即i>1,rank[i]>1,h[i-1]>1.那么我们在计算suffix(i)与suffix(rank[i]-1)的lcp时,至少有h[i-1]-1个是相同的。保险起见我们必须从h[i-1]开始比较。而从更新h[i].那么本次比较为:h[i]-h[i-1]+2。
总的比较次数主要为第三部分:
h[1]+1
…(中间可能会有一次rank[i] =1的时候h[i] = 0即只比较1次)
h[i]-h[i-1]+2
h[i+1]-h[i]+2
…
h[n]-h[n-1]+2
累加后
O(c+2*n) = O(n)
所以我们可以得到h数组同时可以得到height数组。借助它们可以求到字符串str的最长的子串,同时获得该子串的位置信息。这样就可以很好的解决问题4了。
后缀数组应用
应用1:模式匹配
利用SA我们可以进行字符串的模式匹配。时间复杂度是O(mlog(len))
其中m是模式串的长度。而len是建立了后缀数组的待匹配字符串的长度。
其实本质是一个二分搜索。
下面介绍复杂度为O(mlogn)的字符串匹配算法。其中m为 模式串的长度。n为待匹配串的长度。首先观察排序后的后缀们:
对于字符串s:ababaaaab有:
rank: 1 index:5 后缀:aaab
rank: 2 index:6 后缀:aab
rank: 3 index:7 后缀:ab
rank: 4 index:2 后缀:abaaaab
rank: 5 index:0 后缀:ababaaaab
rank: 6 index:8 后缀:b
rank: 7 index:3 后缀:baaaab
rank: 8 index:1 后缀:babaaaab其中rank是每个后缀的排名,index是它在s中的位置。我们注意到相邻的后缀们总是“相似”的。什么是相似呢?是指从它们开头往后的字符的ascii码是最相似的(这个“相似”稍后会用到)。更本质的说,后缀串的acsii值是有序排列的。
我们知道字符串的匹配比较也是基于acsii码的。而且根据上述内容,后缀串有序排序。加之之前所说的,字符串s的子串都是s后缀串的前缀。所以,在有序排列的数据中进行查找很自然的想到了二分查找。也即:按照排名不断二分,判断是否相同。
由于m一般是小于等于n的。因为模式串如果长于待匹配模式串,匹配就没有意义了。所以每次二分后匹配的时间复杂度就是O(m)。你只需要按照模式串从前往后一位一位的比较就可以了。而需要二分O(logn)次,因为总共n个后缀串。所以总的复杂度为O(mlogn)。并且输出相关的信息即可。
至此解决了第一、二个问题。
对于第三个问题。
还记得我说的“相似”吗?再看一下下表:
对于字符串s:ababaaaab有:
rank: 0 index:4 后缀:aaaab
rank: 1 index:5 后缀:aaab
rank: 2 index:6 后缀:aab
rank: 3 index:7 后缀:ab
rank: 4 index:2 后缀:abaaaab
rank: 5 index:0 后缀:ababaaaab
rank: 6 index:8 后缀:b
rank: 7 index:3 后缀:baaaab
rank: 8 index:1 后缀:babaaaab假设我们模式串为ab的。
首次二分,我们对应到了abaaaab发现符合(rank4部分)。因为从头到尾依次匹配结果都是正确的。注意到在abaaaab排名前后,都是和abaaaab最接近的(从头到尾模式最相近,这其实本质是由ascii排序结果导致的!)。如图rank5\rank6部分。
这里我们可以得到一个显然的结论:
对于我们要找的模式串,以该模式串开头的后缀们的名次一定是紧邻的。
因此如果我们“统计S中出现T的位置和次数”。我们可以进行如下操作:
一旦找到了第一个符合条件的后缀,我们依次按照名次向前、向后搜索即可。这样就可以找到所有的匹配结果。
注:“相似”的概念只是便于理解。如果直接按照ascii排序特性来看,可以无视该概念。
补充:此外的字符串匹配算法还有:kmp(O(m+n))和bm算法(也就是经典的好后缀、坏字符算法)都是字符串匹配算法。
#include
for (j = 1, p = 1; p < n; j *= 2, m = p)
{
for (p = 0, i = n - j; i < n; i++) y[p++] = i;
for (i = 0; i < n; i++) if (sa[i] >= j) y[p++] = sa[i] - j;
for (i = 0; i < n; i++) wv[i] = x[y[i]];
for (i = 0; i < m; i++) Ws[i] = 0;
for (i = 0; i < n; i++) Ws[wv[i]]++;
for (i = 1; i < m; i++) Ws[i] += Ws[i - 1];
for (i = n - 1; i >= 0; i--) sa[--Ws[wv[i]]] = y[i];
for (t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i = 1; i < n; i++)
x[sa[i]] = cmp(y, sa[i - 1], sa[i], j) ? p - 1 : p++;
}
return;
}
int main()
{
string str;
cin >> str;
cout << str << endl;
int len = str.size();
get_SA(str, sa, len + 1, 130);
for (int i = 1; i <= len; ++i)
cout << sa[i] << endl;
string aa = "ab";
cout << " --- "<< endl;
cout << contain(str,sa,aa) << endl;
return 0;
} 应用2:最长重复子串统计
对于问题4我们曾说过,
“只需要求出字符串s的所有后缀就可间接的表示了s所有的子串”。因为我们的目的就是求出s所有子串中最长的重复子串的长度)那么,可以通过比较字符串的s的后缀中相同的前缀就可以求出s中最长的重复子串。
当然暴力法求是可以的对于每个后缀串我们可以用O(n)的暴力法进行求解。而且我们知道在乱序情况下,所有的组合有P(2,n)中,总的复杂度可达O(n^3),无法接受。而且,这样的话我们就不能很好的利用后缀数组(有序后缀之间是有关联的)的性质了。为此我们引入height数组。
总结
后缀数组之所以这么强大,根本原因在于充分的利用了基数排序和倍增算法的特点。同时特别得益于有序后缀(有序即可二分)的优势以及后缀与子串关系的优势。