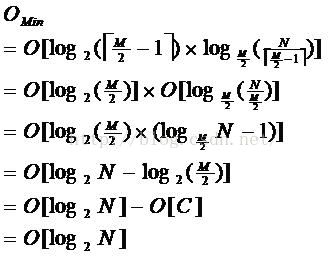数据结构之几种简单树的区别
本科学的数据结构,当时学的挺不错的,随着接触的东西越来越多,树这部分的知识优点混淆了,B树、B+树、B-树、红黑树、平衡二叉树等等,这其中的区别和共性让我有点晕头转向,今天在家看到了,想借此机会总结一下。
当B树平衡的时候,其搜索效率逼近二分查找,并且相比于连续内存空间存储的二分查找的优点在于,改变B树的结构(即插入或者删除操作)不需要移动大段的内存数据,甚至通常是常数开销。
这是一个递归的定义,能充分表明二叉树的限制条件。
结构如下图:
1. B树和平衡二叉树:
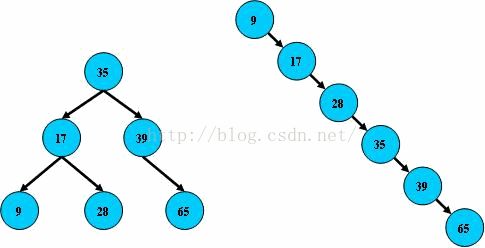
B树是二叉查找树(Binary Search Tree),又叫二叉排序树(Binary Sort Tree),形成B树需要满足三个条件:
| 1、所有非叶子结点至多拥有两个儿子(Left和Right); |
| 2、所有结点存储一个关键字; |
| 3、非叶子结点的左指针指向小于其关键字的子树,右指针指向大于其关键字的子树; |
但是如果没有
限制的话,多次的插入和删除可能会导致树的结构出现变化,最极端的就如下图所示,其搜索效率为线性。
为了达到二分查找的效率,所以我们引入了一些限制,即平衡的概念来保证其效率,所以有了平衡二叉树。
平衡二叉树也是一种二叉树,形成平衡二叉树也需要满足一些条件来保持平衡:
| 它是一 棵左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。空树也是平衡二叉树。 |
2、平衡二叉树和红黑树
平衡二叉树的定义前面已经说了,如何保证其平衡有多种算法。
单纯的平衡二叉树对搜索没有太大用处,只有平衡二叉搜索树才能提高其搜索效率。顾名思义,平衡二叉查找树融合了平衡二叉树和二叉查找树的特点,能够高效的进行查找操作,并且改变树的结构时能保证树的平衡性。而实现这种平衡二叉查找树有多种算法,红黑树是其中一种,另外还有AVL算法。
这里我们简要介绍一下红黑树,作为一种自平衡二叉查找树,它的实现有点复杂,但是实践中是非常高效的,可以在O(logN)时间
内做查找、插入和删除。红黑树要满足五个条件:
| 1、节点是红色或者是黑色的; |
| 2、根一定是黑色的; |
| 3、所有叶子节点一定是黑色的,并且为null; |
| 4、每个红色节点的子节点一定是黑色的; |
| 5、从任一节点到其叶子节点的所有简单路径都包含相同数目的黑色节点。 |
3、 B树、B+树、B-树
B树的定义前面已经说明了,B+和B-树是一种多路搜索树,并不是二叉树。下面的东西我也是从网络上找的:
B-树
是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子;且M>2;
2.根结点的儿子数为[2, M];
3.除根结点以外的非叶子结点的儿子数为[M/2, M];
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字;(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1;
6.非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
7.非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
8.所有叶子结点位于同一层;
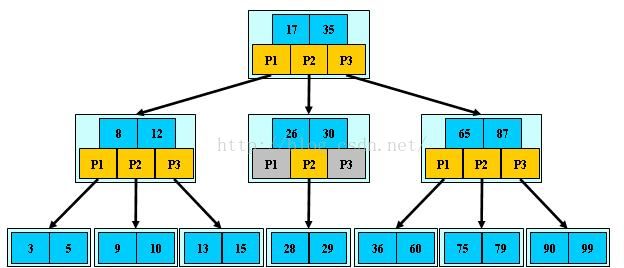
如:(M=3)
B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果
命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为
空,或已经是叶子结点;
B-树的特性:
1.关键字集合分布在整颗树中;
2.任何一个关键字出现且只出现在一个结点中;
3.搜索有可能在非叶子结点结束;
4.其搜索性能等价于在关键字全集内做一次二分查找;
5.自动层次控制;
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少
利用率,其最底搜索性能为:
其中,M为设定的非叶子结点最多子树个数,N为关键字总数;
所以B-树的性能总是等价于二分查找(与M值无关),也就没有B树平衡的问题;
由于M/2的限制,在插入结点时,如果结点已满,需要将结点分裂为两个各占
M/2的结点;删除结点时,需将两个不足M/2的兄弟结点合并;
B+树是B-树的变体,也是一种多路搜索树:
1.其定义基本与B-树同,除了:
2.非叶子结点的子树指针与关键字个数相同;
3.非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
(B-树是开区间);
4.为所有叶子结点增加一个链指针;
5.所有关键字都在叶子结点出现;
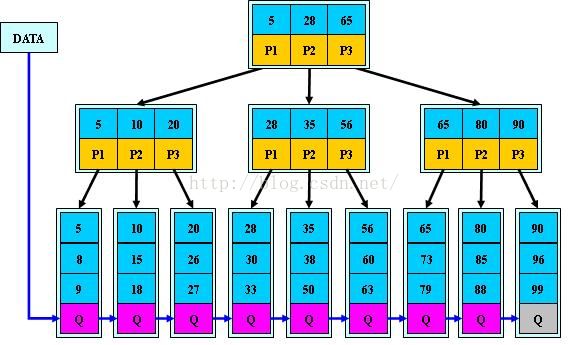
如:(M=3)
B+的搜索与B-树也基本相同,区别是B+树只有达到叶子结点才命中(B-树可以在
非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+的特性:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好
是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储
(关键字)数据的数据层;
4.更适合文件索引系统。
4、 AVL树和红黑树
AVL数和红黑树都是平衡二叉搜索树,只是他们的实现算法不同,AVL树较红黑树算简单的,下面介绍一下原理:
AVL树本质上就是一颗带有平衡条件的二叉查找树,为了保证其查找效率,每次数的结构出现变化(插入删除操作),我们要让保证其仍然平衡。这就需要在插入和删除之后,要判断其是否仍然平衡,如果不平衡,使其平衡。
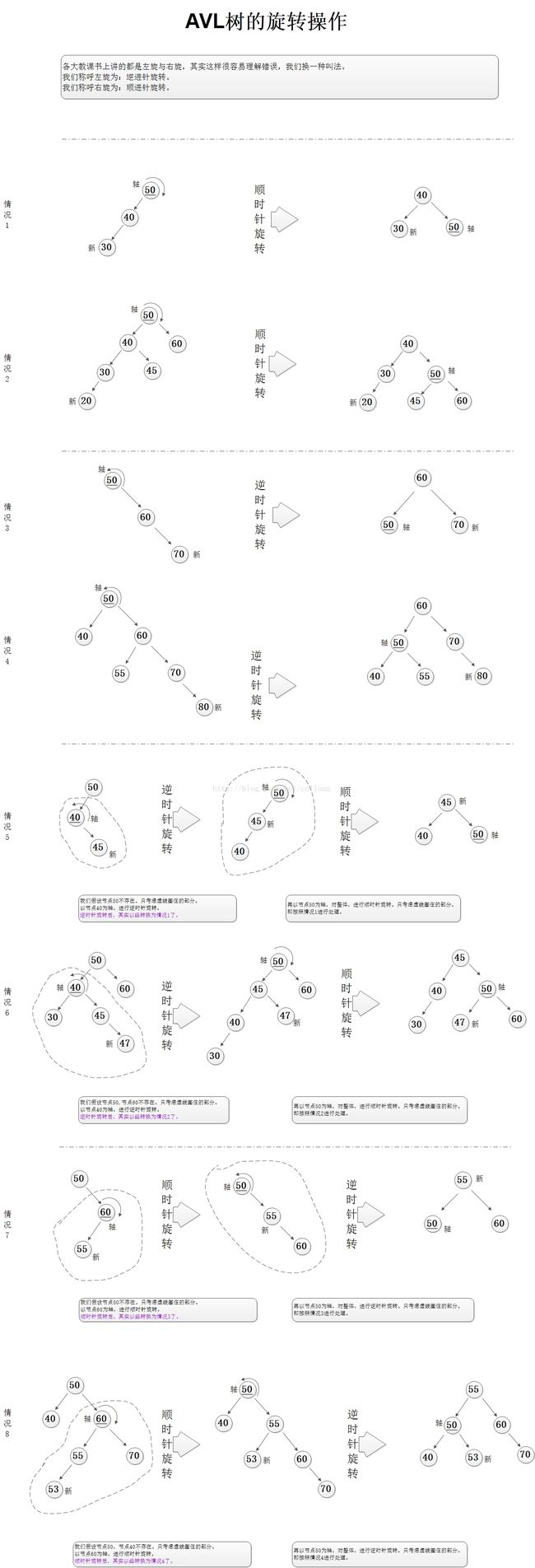
首先说下插入(其实删除和插入一样),在插入的时候,首先来找出其最小的不平衡子树,然后分四种情况进行旋转,大致如下图:
此图来自于 http://blog.csdn.net/collonn/article/details/20128205
图中可以总结一下:
情况1、2为左左,顺时针转;
情况3、4为右右,逆时针转;
情况5、6为左右,先逆时针转成左左,再顺时针转;
情况7、8为右左,先顺时针转成右右,再逆时针转;
这个AVL树原理看起来很简单,但是实现起来并不容易,有兴趣的同学可以尝试一下(先实现个二叉查找树,这个简单,再进行旋转之类的实现)。
红黑树:前面大致说了下红黑树的概念,红黑树的插入和删除的时间复杂度都是O(logN),效率很高;
红黑树的应用也很广泛:
①著名的linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块
②epoll在内核中的实现,用红黑树管理事件块
③nginx中,用红黑树管理timer等
④Java的TreeMap实现
想要深入了解,看看这个博客(http://blog.csdn.net/chenhuajie123/article/details/11951777)吧,感觉红黑树挺复杂的。有空了单独写一篇。