TensorFlow 快速入门

TensorFlowNotes

github
面向普通开发者的机器学习入门

环境搭建

• 操作系统：以Window 64bit 为例（Window、MacOS、Linux都以支持TensorFlow安装）
• python环境搭建
• TensorFlow安装

python环境搭建

注意： 目前Window用户只能使用python3.5（64bit）。MacOS，Linux支持python2.7和python3.3+

具有python基础的可以跳过这一步（如果是Window环境，需要注意对应版本）。

无python基础的强烈推荐使用Anaconda（可以认为是python的集成环境）进行搭建：

• 下载地址，Anaconda3_4.2.0 对应 python3.5
• Window下安装 Anaconda 后(过程略)，会自动将相关路径添加至环境变量中
• （新起的）命令行窗口中输入：conda list 可以查看已集成好的一些环境，如Python、Pip
• 如果你没有比较熟悉的用于开发Python的IDE，可以先使用自带的：Jupyter Notebook（在安装目录的子目录Scripts中即可找到）

知识点：要求了解 Anaconda 、 Pip、Jupyter Notebook 的基本使用

TensorFlow安装

Windows 环境下安装

• CPU版本

  “黑窗口”中运行指令：

pip install tensorflow

• GPU版本

  “黑窗口”中运行指令：

pip install tensorflow-gpu

由于GPU版本还需要进行对应环境的支持，因此暂不在本篇文章说明，我们仅安装CPU版本即可。

环境验证

可以在 python环境的黑窗口中运行：

无报错即表明以上环境皆安装成功，接下来可以准备正式开启TenserFlow之旅了。

---

前提条件和准备工作

参照官方对于机器学习入门的建议

主要是要求基本一定的 数学基础（本科课程能力）与python编程基础。你可以先刷一遍官方文档，也可以在后续的文章中，根据提到的知识点进行学习（对自己的知识体系进行查缺补漏）。

TensorFlow 基本概念

官方中文文档， 以下内容为个人笔记（概要）

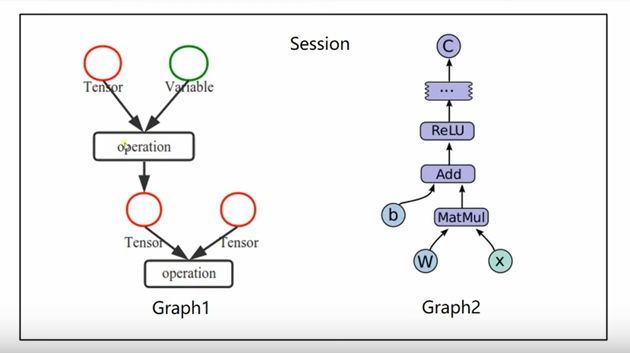
使用 TensorFlow, 你必须明白 TensorFlow:

• 使用图 (graph) 来表示计算任务.
• 在被称之为 会话 (Session) 的上下文 (context) 中执行图.
• TensorFlow 程序使用 tensor(张量)数据结构来代表所有的数据。tensor 看作是一个 n 维的数组或列表. 一个 tensor 包含一个静态类型 rank, 和 一个 shape.
• 通过 变量 (Variable) 维护状态.
• 使用 feed 和 fetch 可以为任意的操作(arbitrary operation) 赋值或者从其中获取数据.

TensorFlow 是一个编程系统, 使用图来表示计算任务. 图中的节点被称之为 op (operation 的缩写). 一个 op 获得 0 个或多个 Tensor, 执行计算, 产生 0 个或多个 Tensor. 每个 Tensor 是一个类型化的多维数组. 例如, 你可以将一小组图像集表示为一个四维浮点数数组, 这四个维度分别是 [batch, height, width, channels].

从Demo入手

以上的概念对于新手可能会有些抽象， 不过没关系，我们可以借助代码来理解。当前环境使用的是：

• Window 7 (64bit)
• TensorFlow 1.7.0
• Python 3.5.2 :: Anaconda 4.2.0 (64-bit)

构建并启动图

一个简单的矩阵相乘：

import tensorflow as tf

# 创建常量 op (图中节点)
m1 = tf.constant([[3,3]])    # 一行两列矩阵 ：（3  3）
m2 = tf.constant([[2],[3]])  # 两行一列矩阵

# 创建一个矩阵乘法op， 把m1和m2传入
product = tf.matmul(m1,m2)   

# 得到一个Tensor对象：Tensor("MatMul:0", shape=(1, 1), dtype=int32)。形状为一行一列的矩阵
print(product) 

# 定义一个会话，启动默认的图 (常用写法,无需手动关闭会话)
with tf.Session() as sess:
    # 执行以上的op
    result = sess.run(product)
    print(result)  # 输出为：[[15]]。 注意： 运行'product' 才真正进行数值计算得到结果

• 构建图 ：第一步, 是创建源 op (图中节点). 源 op 不需要任何输入, 例如 常量 (Constant). 源 op 的输出被传递给其它 op 做运算.

• 启动图 ： 构造阶段完成后, 才能启动图. 启动图的第一步是创建一个 Session 对象, 如果无任何创建参数, 会话构造器将启动默认图.

  ​

常量与变量

# 创建常量 op
m1 = tf.constant([[3,3]])

# 声明一个变量, 初始化为标量 0.
state = tf.Variable(0, name="counter") 

# 启动图, 运行 op
with tf.Session() as sess:
  # 启动图后, 变量必须先经过`初始化` (init) op 初始化,
  sess.run(tf.initialize_all_variables())

  # to do something...

变量使用前必须运行图进行相应初始化.

加减乘除

这里要求我们掌握 tf 的运算方法的用时，要求我们对矩阵运算有基本的了解。另外，代数相关知识建议看deeplearning 第二章

• 标量 （Scalar） ：一个单独的数
• 向量 （Vector） ：一列数
• 矩阵 （Matrix） ：一个二维数组
• 张量 （tensor） ：在某些情况下，我们会讨论坐标超过两维的数组。

注意： 矩阵乘法函数为：matmul

# 标量、向量
tf.add(2,3)        # 5
tf.subtract(3,2)   # 1
tf.multiply(2,3)   # 6

tf.add([3,3],[2,3])        # [5 6]
tf.subtract([3,3],[2,3])   # [1 0]
tf.multiply([3,3],[2,3])   # [6 9]

# 矩阵(2*2)、张量
tf.add([[3,3],[4,4]],[[2,1],[2,2]])        # [[5 4]  [6 6]]
tf.subtract([[3,3],[4,4]],[[2,1],[2,2]])   # [[1 2]  [2 2]]
tf.matmul([[3,3],[4,4]],[[2,1],[2,2]])     # [[12  9]  [16 12]]

类型转换

函数

# tensor `a` is [1.8, 2.2], dtype=tf.float
tf.cast(a, tf.int32) ==> [1, 2]  # dtype=tf.int32

为了让特定运算能运行，有时会对类型进行转换。例如

tf.subtract(tf.cast(tf.constant(2.0), tf.int32), tf.constant(1))   # 1

线性回归

监督学习主要解决两个方向的问题： 逻辑回归、分类。 现在我们从最简单的线性回归开始说起。

这部分涉及的主要知识点有：

• 损失函数
• 梯度下降法（优化器）

数据（样本）

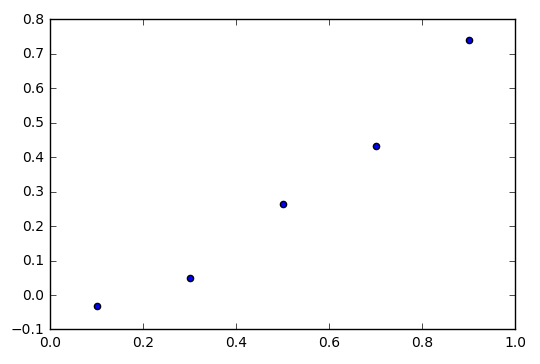
假设我们有以下一组数据:

x_data = np.array([0.1,0.3,0.5,0.7,0.9])  
y_data = np.array([-0.0333,0.0506,0.2633,0.4322,0.7398]) 

（说明：以上数据无任何实际意义，只是为了方便问题说明而随机生成的一些样本点，你可以理解为房屋面积和房价的关系也行，anyway，不影响对知识点的理解）

预测

假设现在要我们根据上面的数据点画一条直线去表示数据的走向，应该是很简单的，大概会是这样：

当然，这个简单的例子中，要我们计算具体的线性方程y = wx + b也不是什么难事。但我们现在的问题是如何让 TensorFlow 帮我们计算这个 w(权重)、b（偏置值）。另外再回顾一个问题：你在画线时是依据什么来判断画的这条直线是最优的（即给一个 x，预测得到的 y 距离真实值将尽可能小）。

代码

既然要用 TensorFlow ，那么废话少说，直接上代码：

import tensorflow as tf

# 数据（样本）
x_data = [0.1,0.3,0.5,0.7,0.9] 
y_data = [-0.0333,0.0506,0.2633,0.4322,0.7398]         

# 构造线性模型，我们的目的是让 TensorFlow 帮我们求得 w 与 b 的具体值
w = tf.Variable(0.0) # 权重变量
b = tf.Variable(0.0) # 偏置值变量
y = w * x_data + b

# 损失函数
#
# tf.square(y_data - y) 求平方差 
# reduce_mean           求平均值 
loss = tf.reduce_mean(tf.square(y_data - y))

# 优化器 -- 梯度下降法
optimizer =  tf.train.GradientDescentOptimizer(0.1)

# 训练使loss"最小",即 使预测出来的 w 和 b "最优"
train = optimizer.minimize(loss)

# 常用写法（无需手动关闭会话）
with tf.Session() as sess:
    # 初始化全部变量
    sess.run(tf.global_variables_initializer())

    # 训练
    for step in range(1001):
        sess.run(train)
        if(step % 50 == 0):
            print(sess.run([w,b]))  # 输出预测结果

输出结果为：
[0.0444744, 0.058104005]
[0.5299716, 0.040158607]
[0.7340628, -0.06876528]
[0.842163, -0.12645866]
[0.8994201, -0.15701687]
[0.9297472, -0.17320259]
[0.9458105, -0.18177557]
[0.9543186, -0.1863164]
[0.95882505, -0.1887215]
[0.961212, -0.18999538]
[0.9624762, -0.19067009]
[0.9631458, -0.19102748]
[0.9635005, -0.19121677]
[0.9636885, -0.19131711]
[0.963788, -0.1913702]
[0.96384066, -0.19139834]
[0.96386856, -0.19141322]
[0.96388334, -0.19142106]
[0.9638909, -0.19142513]
[0.9638949, -0.19142729]
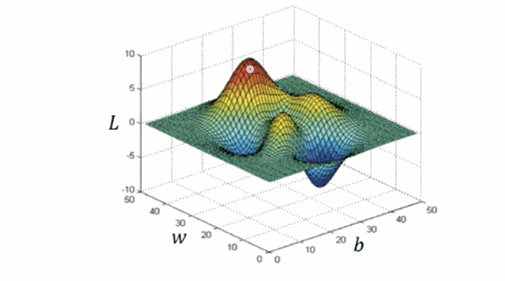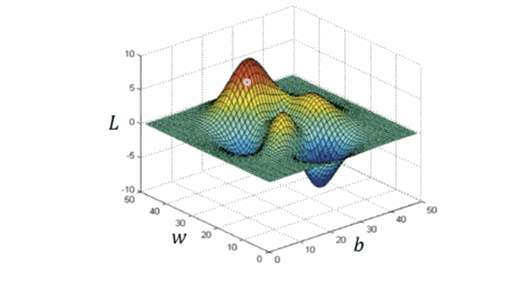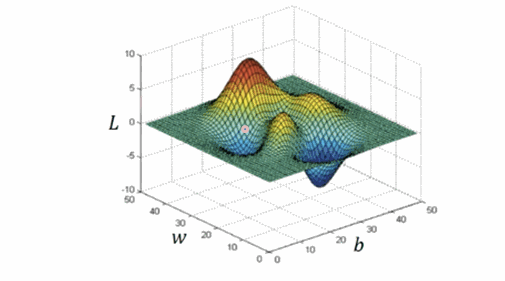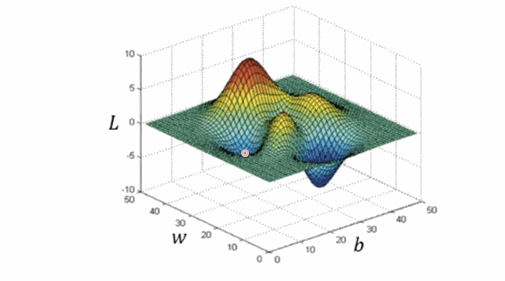
[0.9638976, -0.19142869]

可视化（过程）效果如下，可以看到 TensorFlow ”预测“的演变过程，最终稳定在一个值（到达山脚）（图像采用 matplotlib.pyplot 进行绘制，详细代码见：example/code1.py）：

损失函数

参考资料

还记的前面的问题 你在画线时是依据什么来判断画的这条直线是最优的 吗? 损失函数就是我们判断的依据。损失函数（loss function）是用来估量你模型的预测值 f(x) 与真实值 Y 的不一致程度，它是一个非负实值函数，损失函数越小，模型的鲁棒性就越好。

上面代码中我们使用的是：平方损失函数（最小二乘法, Ordinary Least Squares ）。 按照上面的例子，其实我们求的就是一个均方差（MSE）tf.reduce_mean(tf.square(y_data - y))，即计算预测值 y 与我们的真实值 y_data 的平方和的平均数。所以，很显然，当我们的损失函数的值越小，那么我们得到的方程（模型）将越好。

另外还有几种常见的损失函数：

• 平方损失函数（最小二乘法, Ordinary Least Squares ）：假设样本是 高斯分布的条件下推导得到

• log对数损失函数（逻辑回归）：假设样本服从伯努利分布（0-1分布）

• 指数损失函数（Adaboost）
• Hinge损失函数（SVM）

优化器(optimizer)

我们接下来的目标就是使损失函数的值”最小”，那么演员—优化器(optimizer) 上场。TensorFlow 为我们封装了很多优化器， 比如我们代码中使用的就是梯度下降算法优化器（GradientDescentOptimizer）。关于梯度下降打个比方：假设我们站在某个山坡上，梯度下降算法就可以帮助我们找到最快下山的途径，当然这个“最快”可能只是局部最优解。

另外，梯度下降相关可以观看 Andrew Ng 课程： 监督学习应用.梯度下降。 这节课（26:15 开始讲梯度下降）中同样介绍了损失函数相关概念，如果你对深度学习有浓厚兴趣，强烈建议观看这系列课程。顺带扯几句：该系列课程，主要是介绍了深度学习的相关概念，并且带着一步步推导相关算法，推导过程可能比较费时费力，所以你也可以选择先把整体概念过一遍后，根据实际需要慢慢啃这些算法。

常见优化器如下：

• AdadeltaOptimizer
• AdamOptimizer
• MomentumOptimizer
• RMSPropOptimizer

博客推荐：如何选择优化器 optimizer

以上部分即为最简单的一个“实战”了。主要概念是：损失函数、优化器。

待续

• 神经网络
• 激活函数
• 过拟合

参考资料

[1] 官方机器学习速成课程（中文）

[2] Tenserflow 教程系列(视频) — 莫烦

[3] tensorflow (视频) — 炼数成金 (需要科学上网)

[4] 《Tensorflow 实战Google深度学习框架》 — 郑泽宇 / 顾思宇

[5] 《Deep Learning 中文翻译》

[6] 机器学习的动机与应用 — Andrew Ng

简要说明： [1] 官方课程，带你快速过一遍机器学习的相关概念，个人觉得效果一般（结合其它教程服用效果更佳）。[2]、[3]、[4] 都是的 TensorFlow 入门教程，自行选择一个进行学习（个人做法是先学完一个，再借助另外两个进行回顾和知识点补充）。[5] 深度学习圣经 : ) 。[6] 斯坦福大学公开课，大佬’网红‘不解释。 [2、3、4]偏重工程实践，[5、6]偏重基础概念、理论讲解，个人认为没有严格的前后顺序，大可进行交叉学习。