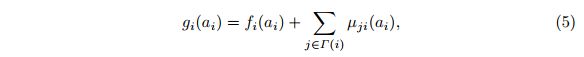读书笔记 - Max-Plus Algorithm

Using the Max-Plus Algorithm for Multiagent Decision Making in Coordination Graphs

协作图通过将global payoff function分解为local terms的总和，为协作多代理决策提供了易于处理的框架。
原则上，每个代理可以基于图的 变量消除算法variable elimination algorithm 来选择最佳个体动作。这就产生了组的最佳行为，但其最坏情况时间复杂度是代理数量的指数，并且在密集连接的图中它可能很慢。此外，变量消除不适用于实时系统，因为它要求在报告解决方案之前终止完整算法。

在本文中，我们研究了max-plus算法，它是贝叶斯网络中置信传播算法的一个实例，作为变量消除variable elimination的近似变换。在该方法中，代理通过协作图反复交换合适的payoff消息，并基于这些消息计算其各自的动作。

我们证明了该方法收敛于树结构图的最优解，并且它在图中找到接近最优的解，同时比变量消除快得多。

背景

多代理系统（multi-agent system，MAS）由一组彼此交互的代理组成。在这样的系统中，代理单独行动，但结果可能根据其他代理的行为而不同。
在本文中专注于cooperative MAS ，其中代理们尝试优化共享性能，并且必须确保他们选择的个人动作会产生良好的团队效果。
RoboCup【3】 是协作MAS的一个很好的例子，足球机器人必须实时协调他们的行动才能队伍获胜。

最近在多代理协调问题中引入协调图(CG)【4】的概念，它能更方便的处理协调问题。

在此框架中，代理的子集之间的支付函数，其表示代理之间的本地协调依赖性。为了确定最大化局部收益总和的最佳联合作用，在[4]中提出了一种可变消除（VE）算法。
然而，尽管VE是精确的并且总是产生最佳的联合动作，但在某些情况下它可能很慢，并且在最坏的情况下，在密集连接图的代理数量中呈指数级。

在本文中，我们将进一步集中于max-plus算法，该算法类似于贝叶斯网络的置信传播算法，作为VE的近似替代。在这种方法中，代理人反复交换支付消息，在这些消息上他们根据他们的个人行动选择。

Coordination Graphs and Variable Elimination

在本节中，我们将使用变量消除算法(VE)计算一组n个代理的协作行动的问题。
每个代理从一组动作集合$A_i$中选择一个单独的动作 $a_i$，由此产生joint联合动作 a =（a1; …; an） ，并为该团队产生一个payoff回报 u(a)。
协调问题是找到 最大化u(a) 的 最佳联合动作 $a^{\ast }$，即 $a^{\ast }$ = $argma{x}_{a}u(a)$。一种显而易见的方法是枚举所有可能的联合动作并选择最大化u(a)的动作。然而这种方法很快变得不切实际，因为联合动作空间A随着代理数n呈指数增长。

幸运的是，许多问题表现出回报矩阵 u(a) 是稀疏的，每个代理仅依赖于其他代理的一小部分。

利用这种依赖关系可以使用协调图，该协调图将全局回报函数u(a) 分解为 局部回报函数的线性组合，每个局部回报函数仅涉及少数代理。
例如，涉及四个代理的回报函数可以如下分解：

函数 $f_{ij}$ 表示代理动作之间的局部协调依赖性 local coordination dependencies，并且可以映射到图 G=(V, E)，其中V中的每个节点代表代理，而E中的边定义两个代理之间的协调依赖性。
只有互连的代理才能在任何特定实例中协调他们的动作。因此，全局协调问题可以被一些涉及较少代理的局部协调问题所替代。

为了找到最佳联合动作 $a^{\ast }$，我们可以应用 VE（变量消除算法variable elimination algorithm）。该算法如下操作：
– 选择一个代理并收集其邻居所涉及的所有回报函数。
– 接下来，它优化其决策条件 decision conditionally ，即对其邻居的可能行动组合进行优化，并将得到的‘conditional’ payoff function 条件回报函数传递给其邻居。
– 此后，从图中删除该代理。
– 当只剩下一个代理时，此代理会选择一个最大化条件策略的操作。
然后按照相反顺序，其中每个代理基于其条件策略和其邻居的固定动作来计算其最优动作。

举例：
我们首先消除代理1:
此代理依赖于局部回报函数$f_{12}$和$f_{13}$，因此式(1)中 u(a) 的最大化可以写为

代理1定义函数 ${\phi }_{23}(a_2,a_3)=ma{x}_{a1}[f_{12}(a_1,a_2)+f_{13}(a_1,a_3)]$，在给定代理2和3的动作的情况下返回代理1的最大值
最佳响应(条件策略)函数 $B_1(a_2,a_3)=argma{x}_{a1}[f_{12}(a_1,a_2)+f_{13}(a_1,a_3)]$，在给定代理2和3的动作的情况下返回代理1的最佳动作

函数${\phi }_{23}(a_2,a_3)$独立于代理1，于是现在可以将代理1从图中消除。代理1的消除会在代理2和3之间产生新的依赖关系，从而导致图形拓扑的变化。简化式(2)为：
$ma{x}_{a}u(a)=ma{x}_{a_2,a_3,a_4}[f_{34}(a_3,a_4)+{\phi }_{23}(a_2,a_3)]$

接下来，我们应用相同的程序来消除代理2：
由于只有${\phi }_{23}$依赖于代理2，我们定义$B_2(a_3)=argma{x}_{a_2}{\phi }_{23}(a_2,a_3)$
并用 ${\phi }_3(a_3)=ma{x}_{a_2}{\phi }_{23}(a_2,a_3)$ 代替${\phi }_{23}(a_2,a_3)$。于是：

$ma{x}_{a}u(a)=ma{x}_{a_3,a_4}[f_{34}(a_3,a_4)+{\phi }_3(a_3)]$

接下来，我们消除代理3:
我们定义${\phi }_4(a_4)=ma{x}_{a_3}[f_{34}(a_3,a_4)+{\phi }_3(a_3)]$ 。于是：

$ma{x}_{a}u(a)=ma{x}_{a_4}[{\phi }_4(a_4)]$

代理4是最后剩余的代理，并且修正其最佳动作为：
$a_4^{\ast }=argma{x}_{a_4}{\phi }_4(a_4)$

之后执行反向顺序the second pass：
其中每个代理根据其最佳响应(条件策略)函数、以及来自其邻居的固定动作计算其最佳动作。
在我们的示例中，代理3首先选择
$a_3^{\ast }=B_3(a_4^{\ast })$
类似地，我们得到
$a_2^{\ast }=B_2(a_3^{\ast })$
$a_1^{\ast }=B_1(a_2^{\ast },a_3^{\ast })$

在一个代理具有多个最大化最佳响应动作的情况下，它可以随机选择一个，因为它总是将其选择传递给其邻居。

VE的结果与消除顺序无关，并且总能得到最佳联合动作。 此外，VE仅在第二轮结束后产生其最终结果，因此它并不总是适用于必须在时间限制下进行决策的实时多代理系统。

The Max-plus Algorithm

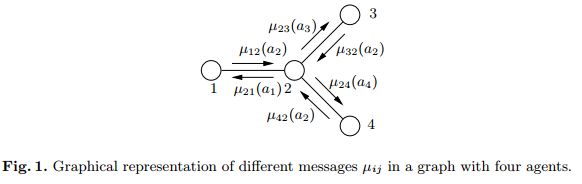
max-plus算法通过在代理 i 和 j 之间迭代地发送消息${\mu }_{ij}(a_j)$来操作，该消息可被视为局部优化的回报函数。
可证明对于树形结构图，消息更新在有限次迭代后收敛到一个固定点。

假设我们有一个协作图 G = (V , E)，|V| 个顶点和 |E| 条边。 V中的节点代替Agent，而全局回报函数可以如下分解：

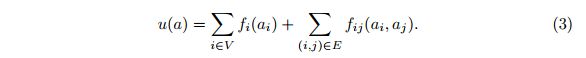
这里$f_i$表示代理i的局部回报函数，并且仅基于其个体动作$a_i$。
此外，e(i , j)表示一对相邻代理(G中的边)。$f_{ij}$是将两个动作 $(a_i,a_j)$ 映射到实数 $f_{ij}(a_i,a_j)$ 的局部回报函数。因此，函数$f_i$表示当代理单独行动时代理对系统的回报。$f_{ij}$代表协调动作的回报。


同样，目标是找到 最大化式(3) 的最佳联合动作 $a^{\ast }$，操作如下：

每个代理 i 重复地向其邻居 j 发送消息 ${\mu }_{ij}$。其中${\mu }_{ij}$将代理 j 的动作$a_j$映射到一个实数，如下所示：

其中 Γ(i)\j 表示除 j 之外的 i 的所有邻居，$c_{ij}$是归一化向量。
该消息可以被近似理解为对于 j 的给定动作，i 可以获得的最大回报。
它可以通过最大化回报函数$f_i$和$f_{ij}$，以及所有传到 i 的消息(除了来自j)的总和来计算。

代理不断交换消息，直到它们收敛为止。

图1显示了具有四个代理和相应消息的CG。

max-plus中的消息${\mu }_{ij}$与VE中的最佳响应(条件策略)有三个重要的区别：
首先，在收敛之前，每条消息都是精确值（条件回报）的近似值，因为它取决于传入的（仍未收敛的）消息。
其次，代理只需要对从邻居收到的消息求和，而不是枚举其邻居的所有可能的动作组合，这使算法易于处理。
最后，在VE中，消除代理通常会导致图拓扑发生变化。在max-plus算法中，消息始终通过原始图的边发送。

对于树，可证明消息在有限步数内可以收敛到一个固定点。
然后，消息${\mu }_{ij}(a_j)$等于代理 j 执行动作$a_j$时，root为代理 i 的子树的回报。

我们还定义了

那么我们可以证明下式成立：

现在每个代理人单独选择其最佳动作 $a_i^{\ast }=argma{x}_{a_i}{g}_i(a_i)$
如果每个代理 i 只有一个最大化动作，则全局最优联合动作 $a^{\ast }=argma{x}_{a}u(a)$ 是唯一的并且$a^{\ast }=(a_i^{\ast })$ 。
可见，该全局最优联合动作可以仅通过局部优化来进行计算（每个节点最大化$g_i(a_i)$）。

（如果局部最大化不唯一，可以通过动态编程技术计算最优联合动作【9】。）

算法实现

max-plus算法都可以在集中式和分布式版本中实现。
在分布式实现中，每个代理在收到来自其邻居的新（不同的）消息之后计算并发送更新的消息。在这种情况下，消息是并行发送的，与集中式算法的顺序执行相比具有计算优势。但是，在分布式实现中由于每个代理必须单独确定系统是否已收敛或何时应报告其动作，因此会产生额外的复杂性。

通常，我们可以假设每个代理接收到“截止时间”信号（来自外部源或来自内部同步定时信号）之后，它必须报告其动作。同时要保证每个局部动作仅在相应的全局回报改善到目前为止找到的最佳回报时才更新。

在 Alg.1 的集中式版本中，我们通过将当前计算的联合动作代入式(3)来计算每次迭代后的全局收益。

在 Alg.2 的分布式版本中，分布式联合动作的evaluation要复杂得多，并且只有当代理认为值得这样做时才会启动。例如，在收到的消息的值大幅增加之后，该代理开始在G中节点的生成树spanning tree ST（该树事先是确定的，并且所有代理都知道）上传播“evaluation”。代理在接收到评估消息后会修正其各自的动作。
当代理人是ST的叶子时，它同样会计算其对全局回报的局部贡献，并将其发送给它ST中的父母。每个父母累积其子女的所有回报，并在添加自己的贡献后将结果发送给其父母。
最后，当ST的根已经从其子节点接收到所有累积的回报时，这些回报的总和（全局回报）被分配给ST中的所有节点。

只有当此回报改善到目前为止发现的最佳回报时，代理才会更新其最佳个人动作$a_i^{\ast }$。
当“截止日期”信号到达时，每个代理不报告对应于当前消息的动作，而是报告与找到的最高全局回报相关的动作。