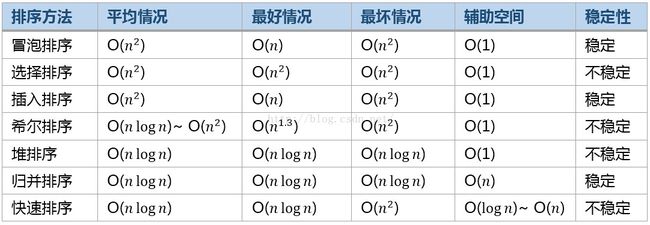
【整理】经典内部排序算法总结和C/C++实现
经典排序算法的掌握是每个程序员的基础,为了巩固下熟练程度和方便自己以后复习,今天来整理下各个排序算法的思路和实现方式。
包括七大排序方法:冒泡排序、选择排序、插入排序、希尔排序、堆排序、归并排序、快速排序。
本文默认待排序列为整型,数组s[]表示,长度为n,排序方法从小到大排序。
一、冒泡排序
思路:遍历待排序列,从前往后(或从后往前)两两比较相邻元素的值,若为逆序则交换位置,直至遍历结束,称为一趟冒泡。一趟冒泡的结果是将最大元素“上浮至”序列末尾,已确定位置的元素不再参与下一趟冒泡过程。重复一趟冒泡的过程,直至序列有序。
步骤:
1.用i遍历数组,初试i为0,即从序列第一个位置开始比较。
2.比较s[i]和s[i+1],若s[i] > s[i+1],交换位置。
3.令i加1,重复步骤2,直至遍历结束。
4.针对所有的元素重复以上的步骤,除了最后一个。
5.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字发生交换。
参考代码:
void Bubble_Sort(int s[],int n)
{
int i,p,temp;
for(p = n;p > 0;p--)
{ bool swap = false; //表示本趟是否发生交换
for(i = 0;i + 1 < p;i++)
{ if(s[i] > s[i+1])
{
temp = s[i];
s[i] = s[i+1];
s[i+1] = temp;
swap = true;
}
}
if(swap == false)
return;
}
}备注:以上的代码还可以优化:记录某次遍历时最后发生数据交换的位置,这个位置之后的数据显然已经有序,不用再排序了。因此通过记录最后发生数据交换的位置就可以确定下次循环的范围了,具体实现略。
二、选择排序
思路:找到数组中最大的元素放在序列末端,再从剩余的元素中继续找到最大元素放在倒数第二个位置,以此类推直至序列有序。
步骤:
1.在0~p的范围内找到最大元素对应的位置m。(初始p为n-1)
2.交换s[m]和s[p]。
3.令p减1,重复步骤1、2。
4.重复上述过程直至序列有序。
参考代码:
void Selection_Sort(int s[],int n)
{
int i,p,m,temp;
for(p = n - 1;p > 0; p--)
{ m = 0;
for(i = 1; i <= p; i++)
{ if(s[i] > s[m])
m = i;
}
if(m != p)
{ temp = s[p];
s[p] = s[m];
s[m] = temp;
}
}
}三、插入排序
思路:对于每个未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
步骤:
1.从第一个元素开始,该元素可以认为已有序。
2.取出下一个元素,在已经排序的元素序列中从后向前扫描。
3.如果被扫描的元素(已排序)大于新元素,将该元素后移一位。
4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置。
5.将新元素插入到该位置后。
6.重复步骤2~5。
参考代码:
void Insertion_Sort(int s[],int n)
{
int i,p,temp;
for(p = 1;p < n;p++)
{ temp = s[p];
for(i = p; i-1 >= 0 && s[i-1] > temp; i--)
s[i] = s[i-1];
s[i] = temp;
}
}四、希尔排序
思路:
我们知道,基于交换的简单排序方法,仅交换相邻元素来排序的话,时间复杂度为O(N2)。每交换一次相邻元素,消除一个逆序对。
希尔又称为缩小增量排序,其基本思想是将待排序列按照增量分成若干个子序列进行插入排序,这样每次交换的不是相邻元素,在时间效率上有所提高。
希尔排序的时间复杂度与增量序列的选取有关,比较复杂不讨论。
参考代码:
以初始步长d为n/2,后续步长为d/2为例:
void Shell_Sort(int s[],int n)
{
int i,p,temp,d;
for(d = n/2;d >= 1;d /= 2)
{ for(p = d;p < n;p++)
{ temp = s[p];
for(i = p; i-d >= 0 && s[i-d] > temp; i -= d)
s[i] = s[i-d];
s[i] = temp;
}
}
}五、堆排序
思路:堆排序算是简单选择排序的优化,区别在于更快的找到待排序列的最大值。简单选择排序通过遍历待排序列数组找到最大元素。而堆排序将待排序列数组调整成大根堆,最大元素即堆顶元素。取出堆顶元素放入队列尾部,然后调整大根堆,重复上述过程直至序列有序。
void Heap_Sort(int s[],int n)
{ int i;
//构造大根堆
for(i = (n - 1) / 2; i >= 0; i--)
Adjust_MaxHeap(s,i,n); //需要一直向下调整,而不是仅仅比较左右孩子节点。
//堆排序,将大根堆转换成有序数组
for(i = 1;i < n;i++)
{ Swap(s[0],s[n-i]);
Adjust_MaxHeap(s,0,n-i);
}
}
void Adjust_MaxHeap(int s[],int i,int n)
{
int m,temp; //m表示左右孩子中较大的一个的下标
temp = s[i];
while(i * 2 + 1 < n) //若不为叶节点,则继续调整
{
m = i * 2 + 1;
if(m + 1 < n && s[m] < s[m + 1])
m++;
if(temp >= s[m])
break;
else
{ s[i] = s[m];
i = m;
}
}
s[i] = temp;
}
void Swap(int &a,int &b)
{
int temp = a;
a = b;
b = temp;
}
六、二路归并排序
思路:将待排序序列看成是n个长度为1的有序序列,将相邻的有序两两归并,得到n/2个长度为2的有序序列;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列。
参考代码:
vector Temp;
void Merge(int left,int leftend,int rightend,int s[]) //合并
{
int i,j;
i = left;
j = leftend+1;
while(i <= leftend && j <= rightend)
{ if(s[i] < s[j])
Temp.push_back(s[i++]);
else
Temp.push_back(s[j++]);
}
while(i <= leftend)
Temp.push_back(s[i++]);
while(j <= rightend)
Temp.push_back(s[j++]);
}
void Merge_Sort(int s[],int n)
{
int i,len;
for(len = 1; len < n;len *= 2) //从长度为1开始,两两归并
{ for(i = 0;i < n;i += len * 2)
{ if(i + len - 1 < n)
{ if(i + len * 2 - 1 < n)
Merge(i,i + len - 1,i + len * 2 - 1,s);
else
Merge(i,i + len - 1,n - 1,s);
}
else
{ while(i < n)
Temp.push_back(s[i++]);
break;
}
}
for(i = 0; i < n; i++) //一趟归并完成后,将临时数组里的数据复制回原数组
s[i] = Temp[i];
Temp.clear(); //清空临时数组
}
} 七、快速排序
快速排序是一般情况下时间复杂度表现最好的排序算法,因此十分常用。
思路:
1.选择一个元素作为基准。
2.调整元素的位置,将比基准元素小的所有元素均移动到它左侧,比基准元素大的所有元素均移动到它右侧。
3.左右区间递归执行第二步,直至各区间只有一个数.
参考代码:
void Quick_Sort(int s[],int left, int right)
{ if(left < right)
{ int PivotPosition = Partition(s,left,right);
Quick_Sort(s,left,PivotPosition - 1);
Quick_Sort(s,PivotPosition + 1,right);
}
}
int Partition(int s[],int left,int right) //一趟排序
{
int pivot = s[left];
while(left < right)
{ while(s[right] >= pivot && right > left) //从右侧查找
right--;
s[left] = s[right];
while(s[left] <= pivot && left < right) //从左侧查找
left++;
s[right] = s[left];
}
s[left] = pivot;
return left; //返回基准存放的位置
}总结: