【干货】在拉斯维加斯，程序员如何靠bandits算法干掉老虎机

作者：友盟+数据科学家 杨玉莲、陆子骏

 

AB测试：从埋点到弃疗

 

AB测试弃疗第一步：

不管是使用频率学派还是贝叶斯学派的方法，我们需要决策还是要走AB测试的一整个流程，但是很多时候使用AB测试来做所有决策的机会成本太高，人力成本太高（数据科学家太贵），较差的版本带来的损失等等原因让使用AB测试做数据驱动沦为了一句口号。

 

AB测试弃疗第二步：

即使一个开发者下定决心走上了利用AB测试做数据驱动的道路，想要搭建一个自有的AB测试平台成本太高，而使用第三方的AB测试服务又缺少灵活的数据分析能力。

如果某个事件没有埋点的话，想要做AB测试就只能SDK重新发版了，在SDK还没有达到一定覆盖率时还是没有办法做AB测试，于是使用AB测试做产品迭代向后延期直到被忘记。AB测试弃疗。

AB测试弃疗第三步：

即使一个开发者用上了友盟+的统计SDK，科学的做了自定义埋点，科学的做了用户的分流，预估了样本数，正确的收集到了数据，正确的做了AB测试，然后发现两个版本并没有区别。或者有时甚至发现新的版本还更差（cue一下被用烂的Facebook的例子）。

作为一个运营你怎么给老板汇报你的负面结果，你作为一个技术团队的大佬怎么抉择改版的问题。AB测试弃疗。我曾经也去问过一个大佬，为什么AB测试这么成熟而有用的方法在中国还不那么普及呢？大佬的说：每一次改版/运营活动后大家都等着去邀功了，谁还想着看数据分析结果呢？

在很多次做AB测试的过程中，还有大佬问有没有迭代更快的AB测试算法呢？有没有不那么严格的AB测试呢？在运营场景的时候被问的最多的问题就是：这个活动就搞3天，你们做AB测试需要多久？你们能不能在运营活动前做AB测试？这类直击灵魂的问题。经过深入的沟通，对于这类问题的AB测试需求其实是希望能够在减少风险的情况下更快的，自动的优化方案。

AB测试疗法

对于这些问题我们有没有什么好的方法去解决呢？当然是有解法的。对于第一和第二步AB测试弃疗的原因的解法只能是进行科学化的埋点首先满足主要的统计需求，因为AB测试是建立在统计模块基础上的。对于AB测试弃疗第三步的解法就是多臂赌博机（Multi-armed bandits）。

多臂赌博机 Multi-armed bandits

那么这种可以自动优化找到最佳方案的算法到底是怎么回事呢？这种算法是如何实现更快的，自动的优化方案的选择呢？

张三在拉斯维加斯

下面我们讲一个张三去拉斯维加斯赌博的故事（毕竟统计学就是起源于赌博）。话说有一天赌徒张三带着自己的积蓄来到拉斯维加斯，想要凭借着自己黑科技眼镜和最近研究的bandits算法赢光拉斯维加斯的赌场成为赌圣。

根据他的多年赌博经验，赌场的每个老虎机的赢率是不同的，但是每个老虎机的赢率是不会变化的，根据江湖传闻这家赌场存在一个老虎机赢率大于50%，他的策略就是找到那个赢率最大的老虎机。

那么张三该如何找到那个赢面最大的老虎机呢？一个最简单的策略就是将赌场里每个老虎机都尝试一遍，然后把每个老虎机的赢率都算一遍，然后选取那个赢率最大的老虎机。这个方法类似于AB测试都是将流量平均的分给了很多个方案。

这个方法的一个明显缺点就是试错成本很高，而且最后才能发现赢率最大的老虎机。如果我们能够在尝试的过程中发现一些方案可能不是最佳，那么我们就不在那些次佳的方案上面浪费时间和精力，那么我们是不是就可以更快的，花更少的钱找到最佳方案呢？那么问题来了，我们应该如何定义哪个算法在寻找最佳方案的时候更优呢？

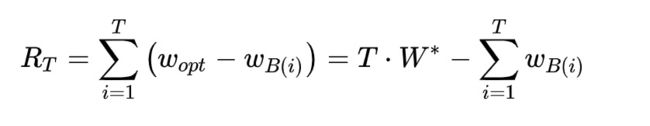
这里计算的就是如果知道最佳方案的赢钱数减去bandits算法在探索最佳方案的赢钱数的差。

张三的bandits算法

张三作为一个赌徒自然是知道一些bandits的算法的，那么他打算使用怎么样的策略呢？他从师傅那里学到的是Epsilon-greedy和Upper bound confidence（UCB）的方法。

Epsilon-greedy的算法就是Epsilon比例的次数选择非最佳的方案，1-Epsilon比例的次数选择当前最佳的方案。Epsilon就是需要人工选择的比例，比如10%的时候都是选择非当前最佳的方案，而90%的时候选择当前最佳的方案。

但是这个方法有一个明显的问题，师傅临行前告诉他使用这个bandits的方法可能会陷入局部的最优解很久都没有办法找到全局最优解，就是不一定能够找到那个赢率最高的老虎机。师傅千叮咛万嘱咐让他小心使用这个bandits 的方法。

于是张三就决定使用UCB这个算法来赌，UCB的算法是怎么实现的呢？

这个是每个老虎机的得分，前面一项就是这个老虎机的平均赢率，第二项是和尝试次数有关的bonus项，其中t是目前实验的次数，而T_{ij}则是这个老虎机被尝试的次数。第二项bonus前还可以有一个系数来调节bonus项的影响大小。

每次实验完成后重新计算每个老虎机的得分然后选择得分最高的那个老虎机进行下一个实验。UCB的bandits算法在足够长的时间是一定可以找到最佳方案的。一般来说UCB的算法在regret的定义下是优于Epsilon-greedy的。

 

李四的bandits算法

话说那边张三还有一个师兄唤做李四，早年曾经在贝老爷子（贝叶斯）门下修习过贝叶斯大法。贝叶斯大法有一个巨大的优势就是它和吸星大法一般可以利用别人修习的成果，这就是贝叶斯里面的先验分布（priors）。

李四在暗中观察着张三在老虎机上的实验并且记录下来每个老虎机的赢率。但是李四也不能等待过久，等到张三发现赢率最大的老虎机的时候他就没法靠那个老虎机赢钱了。于是李四在觉得自己积累够一定数据后下场了，他使用的是基于贝叶斯的Thompson sampling的方法。

在张三尝试的基础上，李四给了每个老虎机了一个基于Beta分布的先验概率，然后自己也开始寻找赢率最大的老虎机，他的每次实验都是基于Beta分布取到一个随机数，然后选择随机数最大的老虎机进行实验。当老虎机积累了更多的数据，Beta分布的方差也越小，每次选取的随机数也更接近于均值，而当老虎机积累了较少的数据时，Beta分布的方差也越大，每次选取的随机数也会忽大忽小。

张三师傅王五的bandit算法

张三的师傅其实也早早来到了拉斯维加斯。他通过内部情报知道其实每个老虎机的赢率是会随着很多因素变化的，比如是否是周末，这个人是男是女等等。

而张三和李四的算法都是没有考虑一些其他的外部因素的，这类考虑其他外部因素的bandits算法叫做contextual bandits。张三师傅使用的是基于UCB算法+ridge regression的LinUCB算法。

欲知张三，李四，王五到底谁最快找到了那个传说中的老虎机，还请继续往下看。

 

bandits和AB测试应该什么时候使用呢？

图来自于VWO的网站

bandits算法主要解决的问题是如何更快的和以更小损失的找到最佳方案。上图就是bandits在寻找最佳方案中的流量分配的优化。bandits能够实现以最小的损失寻找最佳方案。

 

为什么还要做AB测试呢？

首先，AB测试主要用于指导重要的商业决策/产品的版本迭代，而这个决策可能是有很多个指标共同影响的，bandits现在只能是基于单一指标的优化。当然也可以把多个指标叠加成为一个复合指标，但是bandits的优化目标就是单一的一个指标。

其次，AB测试主要适用于获得各个版本的优劣的统计置信（statistical significance）。这么说比较抽象，就是你花了时间开发出来了一个新的版本，你需要确信的知道这个版本到底有没有之前的版本好，到底好在哪里？到底是留存提升了还是用户的使用时长提升了。

这些提升和降低的知识获得是可以使用在产品之后的迭代中的，而bandits是无法帮你分析得到这些知识的。

 

那么什么时候应该用bandits算法呢？

1. 当你关心的问题和张三一样只是转化率，留存率等等的单一指标时并且你不在乎数据结果的解释和分析的时候。

2. 当你的运营活动只有短短的几天或者一天时，你没有时间等到AB测试达到统计置信（statistical significance）的时候，这就是一些大佬们和App开发者提到的更加快的AB测试吧。

3. 还有就是如果你有一些长期需要优化的指标，而这些指标经常发生变化，那么这个也是bandits的一个重要的应用场景。

‍

‍图来自于vwo的blog

总而言之，AB测试适合测试一些变化周期较长的变化，获得的知识应该具有泛化能力。而bandits算法适合一些变化快周期短的优化场景，获得的知识不一定具有泛化能力。

笔者的bandits使用背景

在友盟+的U-Push产品里覆盖了大量的外部用户，而大量的开发者的Push策略都是非常简单的定时广播，而个性的定制化的发送策略几乎没有（除了头条系）。即使开发者想要基于已有的工具对发送时间和发送内容进行优化，现有的标签和用户行为数据积累也不会很充分。

国内的友商们暂时还没有这个功能也是因为他们的数据量远远没有友盟+的数据覆盖度大。而美国的很多针对开发者服务的平台如Recombee，airship，Leanplum等等不仅仅实现了发送时间上的优化，并且实现了基于用户生命周期和其他标签的全链路闭环的用户促活和防流失的产品。

我们未来的工作是为了实现这个非常user-friendly的产品，而我们的起点是对发送时间的优化即LeanPlum的功能。如果我们能够在用户使用App的时候或者是接受Push消息意愿比较强的时候去发送这个消息，那么消息触达用户以后用户也更加愿意打开。这样实现了提高了用户的使用体验和更高的Push点击率的双赢局面。

友盟+的时间优化方案就是基于Thompson sampling的方法，使用Beta分布来给用户+App+时段粒度的打分。

我们发现使用Collaborative filtering能够提高那些数据里没有点击的用户的点击，而Thompson sampling则能够更好的确定那些有点击用户的最佳发送时间。

那么怎么样能够把Collaborative filtering和Thompson sampling结合在一起提高用户的Push体验和点击率将是未来探索的方向。

故事的结局

故事的最后张三，李四，王五都把积蓄都输完了，然后离开了拉斯维加斯，因为他们不知道gambler‘s ruin这个统计原理，这个故事告诉我们还是要远离赌博，小赌不怡情，大赌更伤身。

原文请戳：https://at.umtrack.com/Wnyuqm