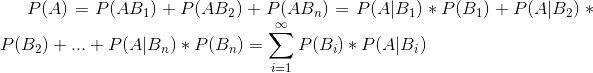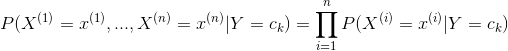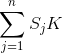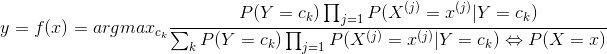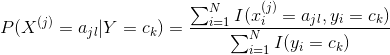统计学习第四章（朴素贝叶斯）知识总结

4.1朴素贝叶斯所用到的数学和概率论知识

  4.1.1概率论基础

         条件概率：

                            

         乘法法则：

                            

                            

                                （A、B互为独立事件）

  4.1.2全概率公式

         释义：求时间A的概率，可以将A、B分解成几个小事件，通过求小事件的概率相加从而得到整个事件A的概率

         公式：

                    

  4.1.3贝叶斯公式推导：

                          由乘法法则得到

                          

                          与全概率公式相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因，也就是事件Bi对于事件A发生的                             影响有多大。

---

4.2朴素贝叶斯模型

          朴素贝叶斯法通过训练数据集学习联合概率分布P(X,Y)，具体地，学习以下先验概率分布（根据以往的经验和分析得到的概率）及条件概率分布，简单的来说就是求某些特征（X）导致的分类结果（Y）的概率。

          先验概率分布：

                            

          条件概率分布：

                     

          由条件概率公式上式=

                           

          根据乘法公式上式=

                                                          

          由上面公式可以看出条件概率分布有指数级数量的参数，参数个数为其估计实际是不可行的。

          所以为了能过计算概率，朴素贝叶斯算法对条件概率分布作出了条件独立性假设，让互相条件独立（有时会牺牲已定的分类准确性），这样条件概率分布变为：

                           

          参数个数也变成了   ，可以进行估计。

         

          朴素贝叶斯法分类时其实就是用上面所说的先验概率来求解后验概率，后验概率公式为：

                                   

---

4.3朴素贝叶斯策略

          朴素贝叶斯的策略是求解模型中分类的后验概率的最大值，概率越高则被分到该类的可能性越大。

          策略公式：

                           

           书中说是上式中分母对所有都是相同的，我是这么理解的：

           分母         是求和 

           由条件概率公式得到

                    

           所以分母与无关，所以可以省略分母，式子变为：

                                    

---

4.3朴素贝叶斯算法

     （1）计算先验概率和条件概率（用极大似然估计方法计算）

                         

                         

                         

     （2）对于给定的实例计算：

                         

     （3）最大化

                       

---

4.4python实现

         用python实现书中的例子（参考）

         

#!/usr/bin/python
# coding=utf-8
import numpy as np


#创建一个列表用于存放所有样本，并且样本内的词不能重复
def createWorldList(data):
    wordSet = set([])      #先创建一个空列表
    for document in data:
        wordSet = wordSet | set(document)  #样本中的不重复数据放入空列表中
    return list(wordSet)

def word2Vec(wordList,inputWord):
    returnVec = [0]*len(wordList)
    for word in inputWord:
        if word in wordList:
            returnVec[wordList.index(word)] = 1    #Python index() 方法检测字符串中是否包含子字符串,有的话返回开始的索引值。在索引位置的数值置1
    return returnVec
def train(trainMatrix,trainLabels):
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    # pAbusive = (sum(trainLabels)+1.0)/(float(numTrainDocs)+2.0*1.0)
    pAbusive = (sum(trainLabels)) / (float(numTrainDocs))   #分类为1的概率
    p0Num = np.zeros(numWords)     #0类更新前矩阵为【0,0,0,0,0,0】
    p1Num = np.zeros(numWords)     #1类更新前矩阵为【0,0,0,0,0,0】

    # p0Denom = 3.0 + len(trainLabels) - sum(trainLabels)
    p0Denom = len(trainLabels) - sum(trainLabels)      #分类为0的个数6
    # p1Denom = 3.0 + sum(trainLabels)
    p1Denom = sum(trainLabels)                         #分类为1的个数9
    for i in range(numTrainDocs):
        if trainLabels[i] == 1:
            p1Num += trainMatrix[i]      #0类更新后p0Num   [3. 2. 1. 1. 2. 3.]
        else:
            p0Num += trainMatrix[i]      #1类更新后p1Num   [2. 3. 4. 4. 4. 1.]

    p0Vect = np.log(p0Num/p0Denom)       #0类的全部概率,用log函数方便计算
    p1Vect = np.log(p1Num/p1Denom)       #1类的全部概率,用log函数方便计算
    return p0Vect,p1Vect,pAbusive


def classify(vec2clssify,p0Vect,p1Vect,pclass1):
    p1 = sum(vec2clssify*p1Vect) + np.log(pclass1)
    p0 = sum(vec2clssify*p0Vect) + np.log(1-pclass1)
    if p1>p0:
        return 1
    else:
        return 0

def main():
    data = [[1,'s'],[1,'m'],[1,'m'],[1,'s'],[1,'s'],[2,'s'],[2,'m'],[2,'m'],[2,'l'],[2,'l'],[3,'l'],[3,'m'],[3,'m'],[3,'l'],[3,'l']]
    labels = [0,0,1,1,0,0,0,1,1,1,1,1,1,1,0]
    wordList = createWorldList(data)   #把样本中的不重复数据存入到列表中，找出其中的特征值[1, 2, 'm', 3, 's', 'l']
    dataMatrix = []      #数据矩阵
    for item in data:
        dataMatrix.append(word2Vec(wordList,item))
    p0,p1,pAB = train(dataMatrix,labels)
    goal = [2,'m']       #输入的预测用例
    wordVec = np.array(word2Vec(wordList,goal))
    print(classify(wordVec,p0,p1,pAB))

if __name__ == '__main__':
    main()

    最后通过改变变量goal来进行不同的预测，本次预测用例为[2,'m']，结果预测为1类                                                                                                          

---

4.5参考文献

         《统计学习方法》 作者：李航

         《统计学习方法》-朴素贝叶斯法笔记和python源码

           极大似然估计