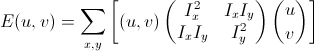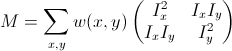Harris角点及Shi-Tomasi角点检测

一、角点定义

有定义角点的几段话：

1、角点检测(Corner Detection)是计算机视觉系统中用来获得图像特征的一种方法，广泛应用于运动检测、图像匹配、视频跟踪、三维建模和目标识别等领域中。也称为特征点检测。


角点通常被定义为两条边的交点，更严格的说，角点的局部邻域应该具有两个不同区域的不同方向的边界。而实际应用中，大多数所谓的角点检测方法检测的是拥有特定特征的图像点，而不仅仅是“角点”。这些特征点在图像中有具体的坐标，并具有某些数学特征，如局部最大或最小灰度、某些梯度特征等。


现有的角点检测算法并不是都十分的鲁棒。很多方法都要求有大量的训练集和冗余数据来防止或减少错误特征的出现。角点检测方法的一个很重要的评价标准是其对多幅图像中相同或相似特征的检测能力，并且能够应对光照变化、图像旋转等图像变化。

2、在我们解决问题时，往往希望找到特征点，“特征”顾名思义，指能描述物体本质的东西，还有一种解释就是这个特征微小的变化都会对物体的某一属性产生重大的影响。而角点就是这样的特征。


观察日常生活中的“角落”就会发现，“角落”可以视为所有平面的交汇处，或者说是所有表面的发起处。假设我们要改变一个墙角的位置，那么由它而出发的平面势必都要有很大的变化。所以，这就引出了图像角点的定义


“如果某一点在任意方向的一个微小变动都会引起灰度很大的变化，那么我们就把它称之为角点”

3、

特征检测与匹配是Computer Vision 应用总重要的一部分，这需要寻找图像之间的特征建立对应关系。点，也就是图像中的特殊位置，是很常用的一类特征，点的局部特征也可以叫做“关键特征点”(keypoint feature)，或“兴趣点”(interest point)，或“角点”(conrner)。

关于角点的具体描述可以有几种：

• 一阶导数(即灰度的梯度)的局部最大所对应的像素点；
• 两条及两条以上边缘的交点；
• 图像中梯度值和梯度方向的变化速率都很高的点；
• 角点处的一阶导数最大，二阶导数为零，指示物体边缘变化不连续的方向。

二、角点检测算法

1、Moravec角点检测算法

Moravec角点检测算法是最早的角点检测算法之一。该算法将角点定义为具有低“自相关性”的点。算法会检测图像的每一个像素，将像素周边的一个邻域作为一个patch，并检测这个patch和周围其他patch的相关性。这种相关性通过两个patch间的平方差之和(SSD)来衡量，SSD值越小则相似性越高。


如果像素位于平滑图像区域内，周围的patch都会非常相似。如果像素在边缘上，则周围的patch在与边缘正交的方向上会有很大差异，在与边缘平行的方向上则较为相似。而如果像素是各个方向上都有变化的特征点，则周围所有的patch都不会很相似。


Moravec会计算每个像素patch和周围patch的SSD最小值作为强度值，取局部强度最大的点作为特征点。

2、Harris角点检测

转载：http://blog.csdn.net/xiaowei_cqu/article/details/7805206
源码及资料下载： http://download.csdn.net/detail/xiaowei_cqu/4466627

当一个窗口在图像上移动，在平滑区域如图(a)，窗口在各个方向上没有变化。在边缘上如图(b)，窗口在边缘的方向上没有变化。在角点处如图(c)，窗口在各个方向上具有变化。Harris角点检测正是利用了这个直观的物理现象，通过窗口在各个方向上的变化程度，决定是否为角点。

将图像窗口平移[u,v]产生灰度变化E(u,v)

由：， 得到：

对于局部微小的移动量 [u,v]，近似表达为：

其中M是 2*2 矩阵，可由图像的导数求得：

E(u,v)的椭圆形式如下图：

 

定义角点响应函数 R 为：

Harris角点检测算法就是对角点响应函数R进行阈值处理：R > threshold，即提取R的局部极大值。

【相关代码】

OpenCV中定义了 cornerHarris 函数：

 void cornerHarris( InputArray src, OutputArray dst, int blockSize,
                                 int ksize, double k,
                                 int borderType=BORDER_DEFAULT );

可以结合 convertScaleAbs 函数，通过阈值取角点：

 void cornerHarris_demo( int, void* )
 {
   Mat dst, dst_norm;
   dst = Mat::zeros( src.size(), CV_32FC1 );
   /// Detector parameters
   int blockSize = 2;
   int apertureSize = 3;
   double k = 0.04;
   /// Detecting corners
   cornerHarris( src_gray, dst, blockSize, apertureSize, k, BORDER_DEFAULT );
   /// Normalizing
   normalize( dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat() );
   convertScaleAbs( dst_norm, dst_norm_scaled );
   /// Drawing a circle around corners
   for( int j = 0; j < dst_norm.rows ; j++ )
      { for( int i = 0; i < dst_norm.cols; i++ )
           {
             if( (int) dst_norm.at<float>(j,i) > thresh )
               {
                 circle( dst_norm_scaled, Point( i, j ), 5,  Scalar(0), 2, 8, 0 );
                 circle(src,Point( i, j ), 5,  Scalar(255,0,0), -1, 8, 0 );
               }
           }
      }
   /// Showing the result
   imshow( corners_window, dst_norm_scaled );
   imshow( source_window, src );
 }

另一篇对Harris的讲解（http://www.cnblogs.com/ztfei/archive/2012/05/07/2487123.html）

 

在我们解决问题时，往往希望找到特征点，“特征”顾名思义，指能描述物体本质的东西，还有一种解释就是这个特征微小的变化都会对物体的某一属性产生重大的影响。而角点就是这样的特征。

观察日常生活中的“角落”就会发现，“角落”可以视为所有平面的交汇处，或者说是所有表面的发起处。假设我们要改变一个墙角的位置，那么由它而出发的平面势必都要有很大的变化。所以，这就引出了图像角点的定义

“如果某一点在任意方向的一个微小变动都会引起灰度很大的变化，那么我们就把它称之为角点”

---

 

由上面定义，我们可以想到算法思路：去检测图像像素的灰度变化情况，即求解　　

，其中，I(x,y)表示像素的灰度值

对于上式，我们希望找到使E的值尽量大的点，则，将上式右边泰勒展开得：

整理可得：

，进而可以表示为下式

这里考虑进去窗函数，设

于是，Harris整理出Harris算子的公式：

，其中M即为上面的矩阵，但是为什么会有这个算子呢，我试着给一点解释。

让我们来重新来考虑矩阵，一切的问题还得回归到数学上去

，这个矩阵先摆在这里，我们先看一下协方差矩阵。

---

　　协方差矩阵的作用为什么比方差和均值要大呢？显而易见方差和均值只是一维随机变量的统计值，而协方差就不一样了，它可以表示多维随机变量之间的相关性信息。协方差矩阵的一个很出色的应用就是在PCA中，选择主方向。协方差矩阵的对角线的元素表示的是各个维度的方差，而非对角线上的元素表示的是各个维度之间的相关性，因此，在PCA中，我们尽量将非对角线上的元素化为0，即将矩阵对角化，选特征值较大的维度，去掉特征值较小的维度，来获得主方向，并且使主方向与其他方向的相关性尽量小。那现在看看这个矩阵M,通过上面对协方差的描述，我们完全可以把这个矩阵看做一个二维随机分布的协方差矩阵，那么我们要做的就是将其对角化，求矩阵的两个特征值，然后根据这两个特征值来判断是不是角点（两个特征值都大代表角点）。

---

而对于Harris算子来说，我们也可以写成下式的形式：

，单单从这个式子中我们无法与上面联系起来，上面是说要让两个特征值都大的点，而这个式子是要求使R最大的点，而也没有办法一眼看出R与两个特征值之间的单调性关系。

---

下面我只是去验证此式的正确性，至于它到底是根据什么构造的，我还不清楚，如果有人知道，请告诉我一下~~

我们这里设，进而可以设，所以,现在我们对求导，整理后可得下式：

，对于k值，我们一般取0.04~0.06，所以对于角点，导数是正的，且随着特征值的增大，导数呈上升的趋势。也就是说这个算子是符合上面的理论分析的。

---

 

像上面这样去求解原则上是没有问题的，可是，众所周知，原始的Harris角点检测算法不具有尺度不变性（也就是说如果图像的尺度发生变化，那么可能原来是角点的点在新的尺度就不是角点了）。

所以，我们在进行运算的开始先将图像转化到尺度空间表示，即将原图像进行尺度变换，而尺度变换的方式就是问题的输入信号与尺度核函数做卷积运算：

，其中这里的运算为卷积运算，不是乘运算。即

，其中sigma表示尺度。然后，我们就使用L代替原图像去进行运算，而尺度成了我们运算的参数了。

---

我们知道Harris角点本身就不受光照，旋转的影响，现在我们又使其满足尺度不变性，所以，Harris角点可以作为一个优秀的特征来帮助我们解决问题。

 

本文只介绍了一下空域上的Harris角点的检测，但是我们现在需要将Harris角点扩展到时空域中，其实道理都差不多，再续！

还有一段对Harris的计算步骤描述：

3、Shi-Tomasi 算法

 

Shi-Tomasi 算法是Harris 算法的改进。Harris 算法最原始的定义是将矩阵 M 的行列式值与 M 的迹相减，再将差值同预先给定的阈值进行比较。后来Shi 和Tomasi 提出改进的方法，若两个特征值中较小的一个大于最小阈值，则会得到强角点。

如上面第二幅图中，对自相关矩阵 M 进行特征值分析，产生两个特征值和两个特征方向向量。因为较大的不确定度取决于较小的特征值，也就是，所以通过寻找最小特征值的最大值来寻找好的特征点也就解释的通了。
Shi 和Tomasi 的方法比较充分，并且在很多情况下可以得到比使用Harris 算法更好的结果。

 

【相关代码】

由于这种Shi-Tomasi算子与1994年在文章 Good Features to Track [1]中提出，OpenCV 实现的算法的函数名定义为 goodFeaturesToTrack：

 void goodFeaturesToTrack( InputArray image, OutputArray corners,
                                      int maxCorners, double qualityLevel, double minDistance,
                                      InputArray mask=noArray(), int blockSize=3,
                                      bool useHarrisDetector=false, double k=0.04 );

自定义使用函数（以方便createTrackbar的响应）如下：

 void cornerShiTomasi_demo( int, void* )
 {
   if( maxCorners < 1 ) { maxCorners = 1; }
   /// Parameters for Shi-Tomasi algorithm
   vector corners;
   double qualityLevel = 0.01;
   double minDistance = 10;
   int blockSize = 3;
   bool useHarrisDetector = false;
   double k = 0.04;
   /// Copy the source image
   Mat cormat;
   /// Apply corner detection :Determines strong corners on an image.
   goodFeaturesToTrack( src_gray,
                corners,
                maxCorners,
                qualityLevel,
                minDistance,
                Mat(),
                blockSize,
                useHarrisDetector,
                k );
   /// Draw corners detected
   for( int i = 0; i < corners.size(); i++ ){
       circle( dst_norm_scaled,  corners[i], 5,  Scalar(255), 2, 8, 0 );
       circle( src, corners[i], 4, Scalar(0,255,0), 2, 8, 0 );
   }

   /// Show what you got
   imshow( corners_window, dst_norm_scaled );
   imshow( source_window, src );
 }

 
 

实践

在主函数中定义两个进度条方便调整阈值：

 namedWindow( source_window, CV_WINDOW_AUTOSIZE );
 createTrackbar( "Threshold: ", source_window, &thresh, max_thresh, cornerHarris_demo );
 createTrackbar( "Max  corners:", source_window, &maxCorners, maxTrackbar, cornerShiTomasi_demo );

 namedWindow( corners_window, CV_WINDOW_AUTOSIZE );
 namedWindow( source_window, CV_WINDOW_AUTOSIZE );
 imshow( source_window, src );

 cornerHarris_demo( 0, 0 );
 cornerShiTomasi_demo( 0, 0 );

这里还需要说的是OpenCV 2.4.2中给的角点检测跟踪的示例代码有些问题，是应为SURF等不再定义在 feature2d模块中，而是legacy和nonfree，所以需要加入引用：

 #include "opencv2/legacy/legacy.hpp"
 #include "opencv2/nonfree/nonfree.hpp"

 

角点检测结果：

蓝色实心点为Harris检测结果，绿色空心圈为goodFeaturetoTrack检测结果。

M特征值分解后每个像素点相减的图（也就是Harris阈值判断的图）如下：

黑色实心点为Harris阈值检测结果，白色空心圈为阈值为27时Shi-Tomasi检测结果。

4、FAST角点检测算法

Smith 和 Brady在1997年提出了一种完全不同的角点提取方法，即“SUSAN (Smallest UnivalueSegment AssimilatingNucleus)”提取算子。SUSAN 提取算子的基本原理是，与每一图像点相关的局部区域具有相同的亮度。如果某一窗口区域内的每一像元亮度值与该窗口中心的像元亮度值相同或相似，这一窗口区域将被称之为“USAN”。计算图像每一像元的“USAN”，为我们提供了是否有边缘的方法。位于边缘上的像元的“USAN”较小，位于角点上的像元的“USAN”更小。因此，我们仅需寻找最小的“USAN”，就可确定角点。该方法由于不需要计算图像灰度差，因此，具有很强的抗噪声的能力。


Edward Rosten and TomDrummond 在2006年提出了一种简单快速的角点探测算法，该算法检测的角点定义为在像素点的周围邻域内有足够多的像素点与该点处于不同的区域。应用到灰度图像中，即有足够多的像素点的灰度值大于该点的灰度值或者小于该点的灰度值。


考虑下图中p点附近半径为3的圆环上的16个点，一个思路是若其中有连续的12个点的灰度值与p点的灰度值差别超过某一阈值，则可以认为p点为角点。

这一思路可以使用机器学习的方法进行加速。对同一类图像，例如同一场景的图像，可以在16个方向上进行训练，得到一棵决策树，从而在判定某一像素点是否为角点时，不再需要对所有方向进行检测，而只需要按照决策树指定的方向进行2-3次判定即可确定该点是否为角点。