形态学滤波（2）：开运算、闭运算、形态梯度、顶帽、黑帽

不多说，先上图

1、形态学概述之二

上一篇介绍了形态学的基本操作膨胀和腐蚀，我们这一篇将利用膨胀和腐蚀操作实现对图像更高级的形态学操作，而这些都是建立在膨胀和腐蚀操作基础之上。 

首先形态学的主要用途是获取物体拓扑和结果信息，它通过物体和结构元素的某些运算，得到物体更本质的形态，在图像处理中的主要应用有： 
(1). 利用形态学的基本运算对图像进行观察和处理，从而达到改善图像质量的目的 
(2). 描述和定义图像的各种几何参数和特征如面积、周长、连通、颗粒度、骨架和方向性 
我们通过腐蚀和膨胀两种基本的形态学操作实现开运算、闭运算、形态梯度、顶帽、黑帽五种形态学操作。

2、具体形态学操作的介绍和原理分析

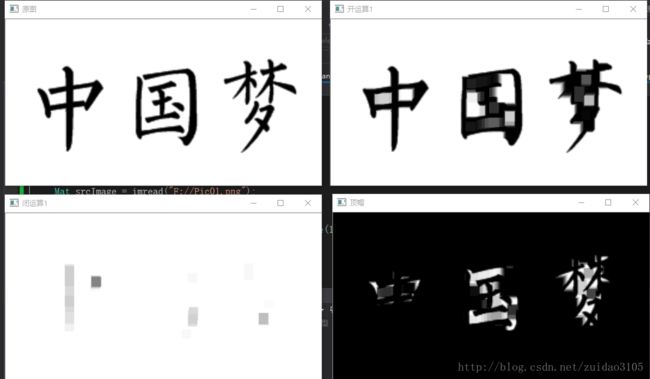
开运算(Opening)

开运算是通过先对图像腐蚀再膨胀实现，其原理表达式如下：

dst=open(src,element)=dilate(erode(src,element))

能够排除小团块物体(假设物体较背景明亮)，开运算的结果删除了不能包含结构元素的对象区域，平滑了对象的轮廓，断开了狭窄的连接，去掉了细小的突出部分。

闭运算(Closing)

闭运算在数学上是先膨胀再腐蚀的结果，其原理表达式如下：

dst=close(src,element)=erode(dilate(src,element))

能够排除小型黑洞(黑色区域)，能够平滑对象的轮廓，但是与开运算不同的是闭运算一般会将狭窄的缺口连接起来形成细长的弯口，并填充比结构元素小的洞。 

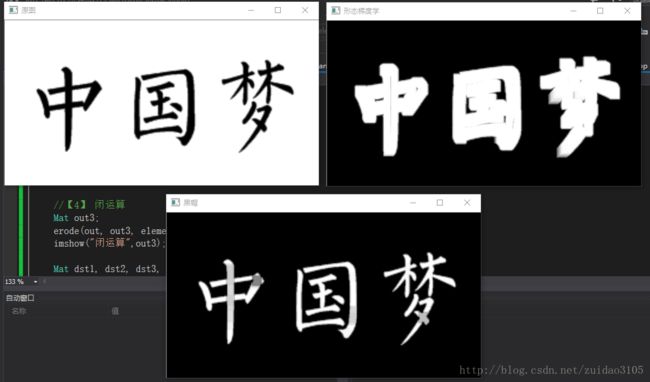
形态梯度(Morphological Gradient)

形态梯度是膨胀图与腐蚀图之差，其操作原理表达式如下：

dst=morph(src,element)=dilate(src,element)-erode(src,element)

形态梯度操作能够保留物体的边缘轮廓

顶帽(Top Hat)

顶帽操作是原图像与开运算结果图之差，其原理表达式如下：

dst=tophat(src,element)=src-open(src,element)

开运算的结果是放大了裂缝或局部降低亮度的区域，因此从原图中减去开运算后的图得到的效果图能够突出比原图轮廓周围的区域更明亮的区域，且这一操作与选择的核的大小有关。 

顶帽操作往往用来分离比邻近点亮一些的板块，在一幅图像具有大幅背景而微小物品比较有规律的情况下，可以使用顶帽运算进行背景提取。

黑帽(Black Hat)

黑帽运算是闭运算结果图与原图像之差，其原理表达式如下：

dst=blackhat(src,element)=close(src,element)-src

黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域，这一操作也与选择的核尺寸有关。所以黑帽运算用来分离比邻近点暗一些的斑块，效果图有着非常完美的轮廓。

opencv中提供了形态学操作函数morphologyEx()来实现开运算、闭运算、形态学梯度、顶帽、黑帽等五种相对高级的操作，也可以实现膨胀核腐蚀两种基本的形态学操作。

3、源代码参考

#include    
#include 
#include 

using namespace cv;
using namespace std;

int main()
{
    Mat srcImage = imread("F://Pic01.png");
    imshow("原图", srcImage);

    Mat element = getStructuringElement(MORPH_RECT, Size(15, 15));

    Mat dst1, dst2, dst3, dst4, dst5, ;

    morphologyEx(srcImage, dst1, MORPH_OPEN, element);
    imshow("开运算", dst1);

    morphologyEx(srcImage, dst2, MORPH_CLOSE, element);
    imshow("闭运算",dst2);

    morphologyEx(srcImage, dst3, MORPH_TOPHAT, element);
    imshow("顶帽", dst3);

    morphologyEx(srcImage, dst4, MORPH_GRADIENT, element);
    imshow("形态梯度学", dst4);

    morphologyEx(srcImage, dst5, MORPH_BLACKHAT, element);
    imshow("黑帽", dst5);

    waitKey(0);
    return 0;
}

效果图

原图

开运算图

闭运算图

形态梯度学图

顶帽图

黑帽图