【文章阅读】【超解像】--Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network
【文章阅读】【超解像】–Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network
论文链接：https://arxiv.org/abs/1609.04802
code(tensorflow)：https://github.com/tensorlayer/srgan
本文将GAN网络引入到了SR应用中，有挺多的创新点，现将文中的主要内容总结如下，后续方便阅读。该主题文章从2016年到2017年一共有5个版本，本文为最新版本V5的阅读理解。
1.主要贡献
针对传统超分辨中存在结果过平滑问题，在PSNR和SSIM评价指标上能得到很好的结果，但图像细节显示依旧较差，利用对抗网络结构的方法，得到了视觉特性上较好结果，本文主要贡献如下：
- 建立了使用PSNR和SSIM为评价标准的SRResNet，对图像进行放大4倍，取得了最好的测试结果。
- 提出了SRGAN网络，该网络结构根据对抗网络网络结构提出了一种新的视觉损失函数(perceptual loss),利用VGG的网络特征作为内容损失函数(content loss),代替了之前的MSE损失函数。
- 对生成的图像进行MOS（mean opinion score）进行评价。
先上图看一下图像最终的图像效果：
2.论文分析
基于CNN的超分辨率方法主要以最优化思想进行目标函数优化，受到目标函数的影响较大。之前的很多研究以最小化平方方差(MSE)作为损失函数，该方法能得到较好的信噪比，但图像会缺失高频信息导致图像的视觉效果差。
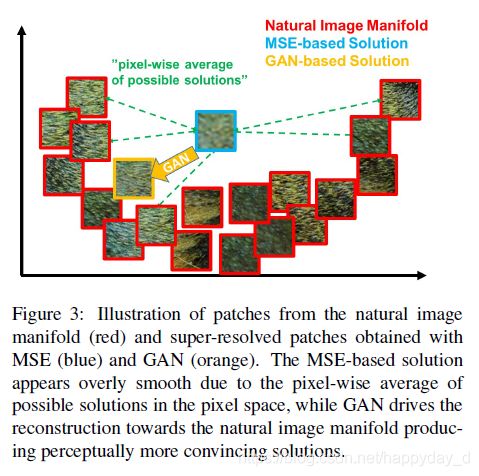
1）用MSE作为损失函数图像模糊
文中解释了为什么MSE为损失函数的图像会损失图像的高频信息，MSE以像素空间的比较为参考，一个低分辨率的图像块可能对应高分辨率中的多个图像块，而GAN只有唯一的对应，这样，通过MSE为目标函数的处理方式会将多个高分辨率的图像块进行平均，所以最终得到的结果有一些模糊。
2） 网络结构
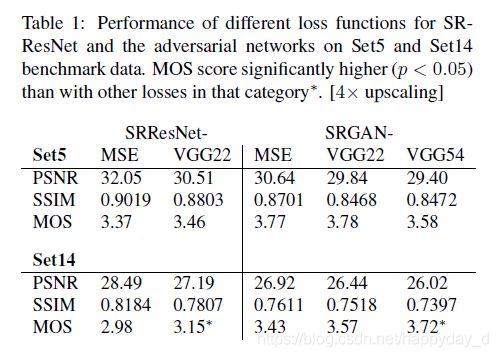
上图上部分为：生成网络结构，基于Resnet网络结构；
上图下部分为：辨别网络结构，利用LeakyReLU(0.2)为激活函数，网络层数从64到512，后面连接两个全连接层和一个sigmoid层，用来判断是否为同一图像的概率；
3）损失函数
(a) 训练生成器和判别器
对给定的HR图像进行降采样得到LR图片，将LR图像作为输入，训练生成器，生成对应的HR图像，该训练过程与训练前馈CNN类似，对网络参数 θ ^ G \hat{{\theta}}_G θ^G 进行优化，如下：
θ ^ G = arg min θ G 1 N ∑ n = 1 N l S R ( G θ G ( I n L R ) , I n H R ) \hat { \theta } _ { G } = \arg \min _ { \theta _ { G } } \frac { 1 } { N } \sum _ { n = 1 } ^ { N } l ^ { S R } \left( G _ { \theta _ { G } } \left( I _ { n } ^ { L R } \right) , I _ { n } ^ { H R } \right) θ^G=argθGminN1n=1∑NlSR(GθG(InLR),InHR)
其中 l S R l^{SR} lSR为视觉损失函数，后面详细介绍。
文中定义的判别器为 D θ G D_{\theta G} DθG，生成器和判别器交替优化如下式子：
min θ G max θ D E I H R ∼ p t a i n ( I H R ) [ log D θ D ( I H R ) ] + E I L R ∼ p G ( I L R ) [ log ( 1 − D θ D ( G θ G ( I L R ) ) ] \min _ { \theta _ { G } } \max _ { \theta _ { D } } \mathbb { E } _ { I ^ { H R } \sim p _ { \mathrm { tain } } \left( I ^ { H R } \right) } \left[ \log D _ { \theta _ { D } } \left( I ^ { H R } \right) \right] +\mathbb { E } _ { I ^ { L R } \sim p _ { G } \left( I ^ { L R } \right) } \left[ \log \left( 1 - D _ { \theta _ { D } } \left( G _ { \theta _ { G } } \left( I ^ { L R } \right) \right) \right]\right. θGminθDmaxEIHR∼ptain(IHR)[logDθD(IHR)]+EILR∼pG(ILR)[log(1−DθD(GθG(ILR))]
(b) 视觉损失函数(perceptual loss function)
本文设计的视觉损失函数，是本文算法性能的保证，如下，分为内容损失(Content loss)和对抗损失(Adversarial loss)
(1) 内容损失
常用的像素级内容损失函数为MSE，如下，该损失函数能取得较高的PSNR，但导致内容缺乏高频图像内容，使最终的显示内容过于平滑。
l M S E S R = 1 r 2 W H ∑ x = 1 r W ∑ y = 1 r H ( I x , y H R − G θ G ( I L R ) x , y ) 2 l _ { M S E } ^ { S R } = \frac { 1 } { r ^ { 2 } W H } \sum _ { x = 1 } ^ { r W } \sum _ { y = 1 } ^ { r H } \left( I _ { x , y } ^ { H R } - G _ { \theta _ { G } } \left( I ^ { L R } \right) _ { x , y } \right) ^ { 2 } lMSESR=r2WH1x=1∑rWy=1∑rH(Ix,yHR−GθG(ILR)x,y)2
文中对内容损失函数进行了改进，在pre-trained 19层 VGG网络(ReLU损失函数)结构基础上定义了VGG loss：
l V G G / i . j S R = 1 W i , j H i , j ∑ x = 1 W i , j ∑ y = 1 H i , j ( ϕ i , j ( I H R ) x , y − ϕ i , j ( G θ G ( I L R ) ) x , y ) 2 \begin{aligned} l _ { V G G / i . j } ^ { S R } = \frac { 1 } { W _ { i , j } H _ { i , j } } & \sum _ { x = 1 } ^ { W _ { i , j } } \sum _ { y = 1 } ^ { H _ { i , j } } \left( \phi _ { i , j } \left( I ^ { H R } \right) _ { x , y } \right. \\ & - \phi _ { i , j } \left( G _ { \theta _ { G } } \left( I ^ { L R } \right) \right) _ { x , y } ) ^ { 2 } \end{aligned} lVGG/i.jSR=Wi,jHi,j1x=1∑Wi,jy=1∑Hi,j(ϕi,j(IHR)x,y−ϕi,j(GθG(ILR))x,y)2
∅ i , j \emptyset_{i,j} ∅i,j表示在VGG19网络中第i个卷积层之前的第j个卷积层(在激活层之后)的特征图，VGG loss是重构图像和参考图像的特征图的欧式距离，上式中的 W i , j W_{i,j} Wi,j和 H i , j H_{i,j} Hi,j表示特征图的维度。
(2)对抗损失
文中将GAN中生成器对视觉损失的影响通过对抗损失来体现，这部分损失函数使我们的网络通过“欺骗”判别器从而生成更接近自然图像的图像。
l G e n S R = ∑ n = 1 N − log D θ D ( G θ G ( I L R ) ) l _ { G e n } ^ { S R } = \sum _ { n = 1 } ^ { N } - \log D _ { \theta _ { D } } \left( G _ { \theta _ { G } } \left( I ^ { L R } \right) \right) lGenSR=n=1∑N−logDθD(GθG(ILR))
其中， D θ D ( G θ G ( I L R ) ) D_{\theta D}(G_{\theta G}(I^{LR})) DθD(GθG(ILR))表示的是判别器将生成的图像 G θ G ( I L R ) G_{\theta G}(I^{LR}) GθG(ILR)判定为自然图像的概率。
3.结果分析
1） MOS评价
MOS为一种主观评价方法，如下图为不同的SR方法的MOS平均意见得分：
2）利用不同的VGG 层作为特征的损失函数性能如下：
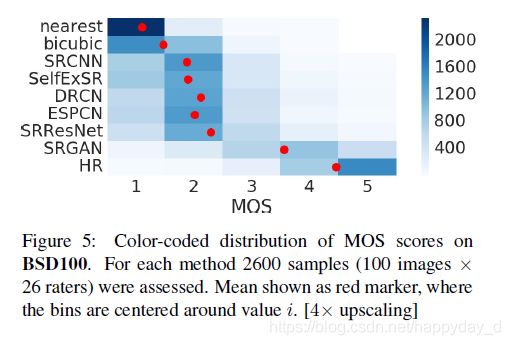
VGG22：表示第2个池化层之前的第2个卷积层，浅层图像特征
VGG54：表示第5个池化层之前的第4个卷积层，深层图像特征
深层图像特征可取得较好的文字细节特征。
4.参考
https://blog.csdn.net/Aaron_wei/article/details/76862038
https://www.cnblogs.com/wangxiaocvpr/p/5989802.html?utm_source=itdadao&utm_medium=referral
论文个人理解，如有问题，烦请指正，谢谢！