数字图像处理第三章 频域处理
数字图像处理第三章 频域处理
- 频域处理
- 1 傅里叶变换（二维离散傅里叶变换推导）
- 2 二维卷积定理
- 3 频率域滤波
- 3.1 频率域滤波步骤
- 3.2 空间和频率域滤波的对应
- 3.3 使用频率域滤波器平滑(锐化)图像
- 3.3.1 理想低通(高通)滤波器
- 3.3.2 高斯低通(高通)滤波器
- 3.3.3 布特沃斯低通(高通)滤波器
- 3.3.4 高频强调滤波
- 4 MATLAB可视化频域处理
- 4.1 观察二维离散傅里叶变换
- 4.2 频率滤波
- 4.3 DFT滤波的基本步骤
- 4.4 从空域滤波器获得频域滤波器
- 4.5 频域中直接生成滤波器
- 4.5.1 建立网格数组以实现频域滤波器
- 4.5.2 频域低通(平滑)滤波器
- 4.5.3 线框及表面绘制
- 4.5.4 高通(锐化)频域滤波器
频域处理
这一章我们要学习的是图像的频域处理，那么到底什么是图像的频率域呢？如果我们把图像看做是一种特殊的二维的信号，那么某一点的灰度级就是这一点的“幅值”，那么图像的频率就是这个图空间上的灰度变换的快慢，或者是叫图像的梯度变化。想要进行图像的频域处理我们就必须要掌握图像在空域和频域的转化，下面就让我们一起来推导傅里叶变换。
1 傅里叶变换（二维离散傅里叶变换推导）
我们从大学课本学习的傅里叶级数出发，法国数学家傅里叶发现，任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示，一般周期为2π的函数傅里叶级数展开为如下形式：
f ( t ) = a 0 2 + ∑ n = 1 + ∞ ( a n c o s n t + b n s i n n t ) , T = 2 π f(t)=\frac{a_0}{2}+\sum_{n=1}^{+\infty}(a_ncosnt+b_nsinnt),T=2π f(t)=2a0+n=1∑+∞(ancosnt+bnsinnt),T=2π之后推广到更一般的形式，不再将周期限制在2π：
φ ( t ) = f ( π l t ) = a 0 2 + ∑ n = 1 + ∞ ( a n c o s n π l t + b n s i n n π l t ) φ(t)=f(\frac{π}{l}t)=\frac{a_0}{2}+\sum_{n=1}^{+\infty}(a_ncos\frac{nπ}{l}t+b_nsin\frac{nπ}{l}t) φ(t)=f(lπt)=2a0+n=1∑+∞(ancoslnπt+bnsinlnπt)其中：
a n = 1 l ∫ − l l f ( t ) c o s n π l t d t , n = 0 , 1 , 2 , . . . a_n=\frac{1}{l}\int_{-l}^l f(t)cos\frac{nπ}{l}tdt,n=0,1,2,... an=l1∫−llf(t)coslnπtdt,n=0,1,2,... b n = 1 l ∫ − l l f ( t ) s i n n π l t d t , n = 0 , 1 , 2 , . . . b_n=\frac{1}{l}\int_{-l}^l f(t)sin\frac{nπ}{l}tdt,n=0,1,2,... bn=l1∫−llf(t)sinlnπtdt,n=0,1,2,...我们想要继续化简φ(t)就要用到被称为最美公式的欧拉公式： e j θ = c o s θ + j s i n θ e^{jθ}=cosθ+jsinθ ejθ=cosθ+jsinθ这里j为复数单位，由欧拉公式我们可以得到:
c o s ω t = 1 2 e j ω t + 1 2 e − j ω t cosωt=\frac{1}{2}e^{jωt}+\frac{1}{2}e^{-jωt} cosωt=21ejωt+21e−jωt s i n ω t = j ( 1 2 e − j ω t − 1 2 e j ω t ) sinωt=j(\frac{1}{2}e^{-jωt}-\frac{1}{2}e^{jωt}) sinωt=j(21e−jωt−21ejωt)我们将上面两个由欧拉公式得到的式子代入化简φ(t)得: φ ( t ) = a 0 2 + ∑ n = 1 + ∞ [ a n 2 ( e j n π l t + e − j n π l t ) − j b n 2 ( e j n π l t + e − j n π l t ) ] = a 0 2 + ∑ n = 1 + ∞ [ a n − j b n 2 e j n π l t + a n + j b n 2 e − j n π l t ] φ(t)=\frac{a_0}{2}+\sum_{n=1}^{+\infty}[\frac{a_n}{2}(e^{j\frac{nπ}{l}t}+e^{-j\frac{nπ}{l}t})-\frac{jb_n}{2}(e^{j\frac{nπ}{l}t}+e^{-j\frac{nπ}{l}t})] \\=\frac{a_0}{2}+\sum_{n=1}^{+\infty}[\frac{a_n-jb_n}{2}e^{j\frac{nπ}{l}t}+\frac{a_n+jb_n}{2}e^{-j\frac{nπ}{l}t}] φ(t)=2a0+n=1∑+∞[2an(ejlnπt+e−jlnπt)−2jbn(ejlnπt+e−jlnπt)]=2a0+n=1∑+∞[2an−jbnejlnπt+2an+jbne−jlnπt]化简到这里我们还没有把an和bn代入就已经很复杂了，于是我们把系数化简一下: C 0 = a 0 2 , C n = a n − j b n 2 , C − n = a n + j b n 2 C_0=\frac{a_0}{2},C_n=\frac{a_n-jb_n}{2},C_{-n}=\frac{a_n+jb_n}{2} C0=2a0,Cn=2an−jbn,C−n=2an+jbn然后我们用Cn去化简φ(t)得: φ ( t ) = C 0 + ∑ n = 1 + ∞ [ C n e j n π l t + C − n e − j n π l t ] φ(t)=C_0+\sum_{n=1}^{+\infty}[C_ne^{j\frac{nπ}{l}t}+C_{-n}e^{-j\frac{nπ}{l}t}] φ(t)=C0+n=1∑+∞[Cnejlnπt+C−ne−jlnπt]我们再把C0看做C0乘e的零次方就可以把上式写成： φ ( t ) = ∑ n = − ∞ + ∞ C n e j n π l t φ(t)=\sum_{n=-\infty}^{+\infty}C_ne^{j\frac{nπ}{l}t} φ(t)=n=−∞∑+∞Cnejlnπt这样我们就把φ(t)化简成了一个特别简单的式子，下面就专心处理系数Cn就好了，由于： a n = 1 l ∫ − l l f ( t ) c o s n π l t d t , n = 0 , 1 , 2 , . . . a_n=\frac{1}{l}\int_{-l}^l f(t)cos\frac{nπ}{l}tdt,n=0,1,2,... an=l1∫−llf(t)coslnπtdt,n=0,1,2,... b n = 1 l ∫ − l l f ( t ) s i n n π l t d t , n = 0 , 1 , 2 , . . . b_n=\frac{1}{l}\int_{-l}^l f(t)sin\frac{nπ}{l}tdt,n=0,1,2,... bn=l1∫−llf(t)sinlnπtdt,n=0,1,2,...代入到Cn的式子之中： C 0 = a 0 2 = 1 2 l ∫ − l l f ( t ) d t = 1 2 l ∫ − l l f ( t ) e − j 0 π t l d t C_0=\frac{a_0}{2}=\frac{1}{2l}\int_{-l}^lf(t)dt=\frac{1}{2l}\int_{-l}^lf(t)e^{-j\frac{0πt}{l}}dt C0=2a0=2l1∫−llf(t)dt=2l1∫−llf(t)e−jl0πtdt C n = a n − j b n 2 = 1 2 [ 1 l ∫ − l l f ( t ) c o s n π l t d t − j 1 l ∫ − l l f ( t ) s i n n π l t d t ] = 1 2 l ∫ − l l f ( t ) e − j n π t l d t C_n=\frac{a_n-jb_n}{2}=\frac{1}{2}[\frac{1}{l}\int_{-l}^l f(t)cos\frac{nπ}{l}tdt-j\frac{1}{l}\int_{-l}^l f(t)sin\frac{nπ}{l}tdt]=\frac{1}{2l}\int_{-l}^lf(t)e^{-j\frac{nπt}{l}}dt Cn=2an−jbn=21[l1∫−llf(t)coslnπtdt−jl1∫−llf(t)sinlnπtdt]=2l1∫−llf(t)e−jlnπtdt C − n = a n + j b n 2 = 1 2 l ∫ − l l f ( t ) e j n π t l d t C_{-n}=\frac{a_n+jb_n}{2}=\frac{1}{2l}\int_{-l}^lf(t)e^{j\frac{nπt}{l}}dt C−n=2an+jbn=2l1∫−llf(t)ejlnπtdt综上 C n = 1 2 l ∫ − l l f ( t ) e − j n π t l d t , n = 0 , ± 1 , ± 2 , . . . C_n=\frac{1}{2l}\int_{-l}^lf(t)e^{-j\frac{nπt}{l}}dt,n=0,±1,±2,... Cn=2l1∫−llf(t)e−jlnπtdt,n=0,±1,±2,...接着我们把化简好的Cn代入φ(t)： φ ( t ) = ∑ n = − ∞ + ∞ 1 2 l ∫ − l l f ( ω ) e − j n π ω l d ω e j n π t l = ∑ n = − ∞ + ∞ 1 2 l ∫ − l l f ( ω ) e j n π ( t − ω ) l d ω φ(t)=\sum_{n=-\infty}^{+\infty}\frac{1}{2l}\int_{-l}^lf(ω)e^{-j\frac{nπω}{l}}dωe^{j\frac{nπt}{l}}\\ =\sum_{n=-\infty}^{+\infty}\frac{1}{2l}\int_{-l}^lf(ω)e^{j\frac{nπ(t-ω)}{l}}dω φ(t)=n=−∞∑+∞2l1∫−llf(ω)e−jlnπωdωejlnπt=n=−∞∑+∞2l1∫−llf(ω)ejlnπ(t−ω)dω到这里我们已经可以把一个周期函数化简到一个非常简单的式子了，但是在实际操作中，很多函数都是非周期函数，对于非周期函数，我们可将其周期视为无穷大： f ( t ) = lim l → + ∞ φ ( t ) = lim l → + ∞ ∑ n = − ∞ + ∞ 1 2 l ∫ − l l f ( z ) e j n π ( t − z ) l d z = lim l → + ∞ ∑ n = − ∞ + ∞ 1 2 π ∫ − l l f ( z ) e j n π ( t − z ) l d z π l f(t)={\lim_{l\to+\infty}}φ(t)={\lim_{l\to+\infty}}\sum_{n=-\infty}^{+\infty}\frac{1}{2l}\int_{-l}^lf(z)e^{j\frac{nπ(t-z)}{l}}dz\\ ={\lim_{l\to+\infty}}\sum_{n=-\infty}^{+\infty}\frac{1}{2π}\int_{-l}^lf(z)e^{j\frac{nπ(t-z)}{l}}dz\frac{π}{l} f(t)=l→+∞limφ(t)=l→+∞limn=−∞∑+∞2l1∫−llf(z)ejlnπ(t−z)dz=l→+∞limn=−∞∑+∞2π1∫−llf(z)ejlnπ(t−z)dzlπ这时就要用到积分的定义，令： ω n = n π l , △ ω = π l ω_n=\frac{nπ}{l},△ω=\frac{π}{l} ωn=lnπ,△ω=lπ继续f(t)的推导: f ( t ) = lim l → + ∞ ∑ n = − ∞ + ∞ 1 2 π ∫ − l l f ( z ) e j ω n ( t − z ) d z △ ω = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( z ) e j ω ( t − z ) d z ] d ω = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( z ) e − j ω z d z ] e j ω t d ω f(t)={\lim_{l\to+\infty}}\sum_{n=-\infty}^{+\infty}\frac{1}{2π}\int_{-l}^lf(z)e^{jω_n(t-z)}dz△ω\\=\frac{1}{2π}\int_{-\infty}^{+\infty}[\int_{-\infty}^{+\infty}f(z)e^{jω(t-z)}dz]dω\\=\frac{1}{2π}\int_{-\infty}^{+\infty}[\int_{-\infty}^{+\infty}f(z)e^{-jωz}dz]e^{jωt}dω f(t)=l→+∞limn=−∞∑+∞2π1∫−llf(z)ejωn(t−z)dz△ω=2π1∫−∞+∞[∫−∞+∞f(z)ejω(t−z)dz]dω=2π1∫−∞+∞[∫−∞+∞f(z)e−jωzdz]ejωtdω推导到这里我们想要的结果已经呈现出来了: 令 F ( ω ) = ∫ − ∞ + ∞ f ( t ) e − j ω t d t 则 f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( ω ) e j ω t d ω 令\quad F(ω)=\int_{-\infty}^{+\infty}f(t)e^{-jωt}dt\\则\quad f(t)=\frac{1}{2π}\int_{-\infty}^{+\infty}F(ω)e^{jωt}dω 令F(ω)=∫−∞+∞f(t)e−jωtdt则f(t)=2π1∫−∞+∞F(ω)ejωtdω上面两个式子就是大名鼎鼎的傅里叶变换对啦，第一个是傅里叶正变换，第二个是傅里叶逆变换，由于我们图像都是离散的像素灰度值，所以我们要得到离散的傅里叶变换对，做N点等距采样可以得到: F ( u ) = ∑ n = 0 N − 1 f ( x ) e − j 2 π u N x f ( x ) = 1 N ∑ n = 0 N − 1 F ( u ) e j 2 π x N u F(u)=\sum_{n=0}^{N-1}f(x)e^{-j\frac{2πu}{N}x}\\f(x)=\frac{1}{N}\sum_{n=0}^{N-1}F(u)e^{j\frac{2πx}{N}u} F(u)=n=0∑N−1f(x)e−jN2πuxf(x)=N1n=0∑N−1F(u)ejN2πxu之后类比拓展到二元函数: F ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x M + v y N ) F(u,v)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2π(\frac{ux}{M}+\frac{vy}{N})} F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy) f ( x , y ) = 1 M N ∑ x = 0 M − 1 ∑ y = 0 N − 1 F ( u , v ) e j 2 π ( u x M + v y N ) f(x,y)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}F(u,v)e^{j2π(\frac{ux}{M}+\frac{vy}{N})} f(x,y)=MN1x=0∑M−1y=0∑N−1F(u,v)ej2π(Mux+Nvy)到此我们就得到了二维离散傅里叶变换对。(以上就为DFT的推导过程，整个过程都是我手打的，可能会出现一些错误，希望发现后指正！)
2 二维卷积定理
在学习频域滤波之前，必须要先了解二维卷积定理，二维循环卷积表达式为： f ( x , y ) ☆ h ( x , y ) = ∑ m = 0 M − 1 ∑ n = 0 N − 1 f ( m , n ) h ( x − m , y − n ) f(x,y)☆h(x,y)=\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)h(x-m,y-n) f(x,y)☆h(x,y)=m=0∑M−1n=0∑N−1f(m,n)h(x−m,y−n)二维卷积定理由下面的表达式给出: f ( x , y ) ☆ h ( x , y ) ⇔ F ( u , v ) H ( u , v ) f(x,y)☆h(x,y)\Leftrightarrow F(u,v)H(u,v) f(x,y)☆h(x,y)⇔F(u,v)H(u,v) f ( x , y ) h ( x , y ) ⇔ F ( u , v ) ☆ H ( u , v ) f(x,y)h(x,y)\Leftrightarrow F(u,v)☆H(u,v) f(x,y)h(x,y)⇔F(u,v)☆H(u,v)其中，F(u,v)与H(u,v)为上一小节f(x,y)与h(x,y)的二维离散傅里叶变换后的函数。
二维卷积定理在使用时可能会产生一种错误被称为缠绕错误，如果不明白什么是缠绕错误一定要自己去了解一下，因为不是具体的一两句话就能解释清楚的，如果用一句话概括就是卷积函数与被处理的图像周期不同而导致它们相互干扰产生的错误被称为缠绕错误。如果你不想去了解，你只需要知道我们在进行频率滤波之前一定要对图像和卷积滤波进行预处理，具体方法如下：令f(x,y)和h(x,y)分别是大小为A×B和C×D像素的图像阵列，循环卷积中的缠绕错误可以通过对这两个函数进行零填充来避免： f p ( x , y ) = f ( x , y ) , 0 ≤ x ≤ A − 1 a n d 0 ≤ y ≤ B − 1 f_p(x,y) = f(x,y),0≤x≤A-1\quad and\quad 0≤y≤B-1 fp(x,y)=f(x,y),0≤x≤A−1and0≤y≤B−1 0 , A ≤ x ≤ P o r B ≤ y ≤ Q 0\quad,A≤x≤P\quad or\quad B≤y≤Q 0,A≤x≤PorB≤y≤Q和 h p ( x , y ) = h ( x , y ) , 0 ≤ x ≤ C − 1 a n d 0 ≤ y ≤ D − 1 h_p(x,y) = h(x,y),0≤x≤C-1\quad and\quad 0≤y≤D-1 hp(x,y)=h(x,y),0≤x≤C−1and0≤y≤D−1 0 , C ≤ x ≤ P o r D ≤ y ≤ Q 0\quad,C≤x≤P\quad or\quad D≤y≤Q 0,C≤x≤PorD≤y≤Q其中， P ≥ A + C − 1 P≥A+C-1 P≥A+C−1和 Q ≥ B + D − 1 Q≥B+D-1 Q≥B+D−1
3 频率域滤波
3.1 频率域滤波步骤
步骤分为7步如下：
(1) 给定一副大小为M×N的输入图像f(x,y),从上一下节用的预处理得到填充P和Q。通常选择P=2M和Q=2N。
(2) 对f(x,y)添加必要数量的0，形成大小为P×Q的填充图像fp(x,y)。
(3) 用(-1)x+y乘以fp(x,y),移到其变换的中心(这里用到了二维离散傅里叶变换的周期性)。
(4) 计算来自步骤3的图像的DFT，得到F(u,v)。
(5) 生成一个实的、对称的滤波函数H(u,v)，其大小为P×Q，中心在(P/2,Q/2)处。用阵列相乘形成乘积G(u,v)=H(u,v)F(u,v);即G(i,k)=H(i,k)F(i,k)。
(6) 得到处理后的图像: g p ( x , y ) = { r e a l [ σ − 1 [ G ( u , v ) ] ] } ( − 1 ) x + y g_p(x,y)=\{real[σ^{-1}[G(u,v)]]\}(-1)^{x+y} gp(x,y)={real[σ−1[G(u,v)]]}(−1)x+y其中的σ-1代表IDFT，为忽略由于计算不准确导致的寄生复成分，选择了实部，下标p指出我们处理的是填充后的阵列。
(7) 从gp(x,y)的左上象限提取M×N区域，得到最终的处理结果g(x,y)。
3.2 空间和频率域滤波的对应
空间域和频率域滤波间的纽带是卷积定理。，我们把频率域中的滤波定义为滤波函数H(u,v)与输入图像的傅里叶变换F(u,v)的乘积。想说明二者之间的关系，我们使用高斯滤波器来说明，高斯函数的正反傅里叶变换都是实高斯函数，我们这里讨论一下一维高斯滤波器，令H(u)表示一维频率域高斯滤波器: H ( u ) = A e − u 2 2 σ 2 H(u)=Ae^{\frac{-u^2}{2\sigma^2}} H(u)=Ae2σ2−u2式中，σ是高斯曲线的标准差。空间域中的相应滤波器有H(u)的傅里叶反变换得到: h ( x ) = 2 π σ A e − 2 π 2 σ 2 x 2 h(x)=\sqrt{2\pi}\sigma Ae^{-2\pi^2\sigma^2x^2} h(x)=2πσAe−2π2σ2x2这里可以看出两个函数是互易的，当H(u)有一个较宽的外形时(σ值较大)，h(x)有较窄的外形，反之亦然。
上图黑色的线是为H(u)，红色的线是h(x)。(这里请忽略坐标和轴单位，因为两个图像的轴单位都是不同的，我只是为了方便对比观察画在了一张图上)，这里我们可以看出来如果H(u)变得更加狭窄，那么在频域中图像通过滤波器的频率范围就会缩小，通过的更多是低频信息，同时h(x)变得更加宽，就像我们在上一章学的高斯模板向box模板演变，像素距离原点的权值影响就会越来越小，图像会越来越模糊，上述变化反过来亦然。
构造完平滑滤波器，我们再用高斯函数构造一个高通滤波器: H ( u ) = A e − u 2 2 σ 1 2 − B e − u 2 2 σ 2 2 H(u)=Ae^{\frac{-u^2}{2\sigma_1^2}}-Be^{\frac{-u^2}{2\sigma_2^2}} H(u)=Ae2σ12−u2−Be2σ22−u2式中，A≥B，σ1＞σ2。空间域中相应的滤波器是: h ( x ) = 2 π σ 1 A e − 2 π 2 σ 1 2 x 2 − 2 π σ 2 B e − 2 π 2 σ 2 2 x 2 h(x)=\sqrt{2\pi}\sigma_1 Ae^{-2\pi^2\sigma_1^2x^2}-\sqrt{2\pi}\sigma_2 Be^{-2\pi^2\sigma_2^2x^2} h(x)=2πσ1Ae−2π2σ12x2−2πσ2Be−2π2σ22x2
上图黑色的线是为H(u)，红色的线是h(x)。(这里请忽略坐标和轴单位）我们可以看到高斯函数构造的高通滤波器对应空间滤波器h(x)的形状就如上一章的拉普拉斯算子形状相似，如果我们去调整两个σ还可以得到跟上面低通类似的性质。
总结：通过了解空间和频率域滤波之间的关系，有些在空间域异常困难的或不可能直接用公式表达的任务，在频域就变得很容易。比如我们要从sin3x+sin5x的曲线中去除sin5x的曲线，但是我们不知道曲线的方程式，在空间域基本上不可能做到的，但在频域就很容易做到。一旦我们在频率域通过实验选择了一个特定的滤波器，那么该方法的实际实现通常是在空间域完成的。
3.3 使用频率域滤波器平滑(锐化)图像
本节的滤波器图片取自我的学姐Dujing2019的频域处理博客
3.3.1 理想低通(高通)滤波器
在以原点为圆心、以D0为半径的圆内，无衰减地通过所有频率，而在该圆外“阻断”所有频率的二维低通滤波器，称为理想低通滤波器(Ideal Lowpass Filter)；它由下面的函数确定： H ( u , v ) = { 1 , D ( u , v ) ≤ D 0 0 , D ( u , v ) > D 0 H(u,v)=\left\{\begin{matrix} 1,D(u,v)\leq D_0 & \\ 0,D(u,v)> D_0 & \end{matrix}\right. H(u,v)={1,D(u,v)≤D00,D(u,v)>D0式中，D0是一个正常数，D(U,V)是频率域中点(u,v)与频率矩形中心的距离，即 D ( u , v ) = [ ( u − P / 2 ) 2 + ( v − Q / 2 ) 2 ] 1 / 2 D(u,v)=[(u-P/2)^2+(v-Q/2)^2]^{1/2} D(u,v)=[(u−P/2)2+(v−Q/2)2]1/2式中，P和Q是前面填充后的尺寸。
这样我们同样可以得到理想高通滤波器(Ideal Highpass Filter) 的函数确定： H ( u , v ) = { 0 , D ( u , v ) ≤ D 0 1 , D ( u , v ) > D 0 H(u,v)=\left\{\begin{matrix} 0,D(u,v)\leq D_0 & \\ 1,D(u,v)> D_0 & \end{matrix}\right. H(u,v)={0,D(u,v)≤D01,D(u,v)>D0实际上为什么称其为理想的滤波器，就是实际上我们是无法达到完全“阻断”的情况，原因与傅里叶变换产生的“振铃”效应有关。
3.3.2 高斯低通(高通)滤波器
二维高斯低通滤波器(Gaussian Lowpass filter) 由下式给出： H ( u , v ) = e − D 2 ( u , v ) / 2 σ 2 H(u,v)=e^{-D^2(u,v)/2\sigma^2} H(u,v)=e−D2(u,v)/2σ2那么二维高斯高通滤波器(Gaussian Highpass filter) 由下式给出： H ( u , v ) = 1 − e − D 2 ( u , v ) / 2 σ 2 H(u,v)=1-e^{-D^2(u,v)/2\sigma^2} H(u,v)=1−e−D2(u,v)/2σ2这是一个很简单的对应，高斯滤波器完美消除了振铃效应，这对于实际工作中任何类型的人工缺陷都不可接受的情况(如医学影像)下，是一个重要的特性，但是需要严格控制低频与高频之间的截至频率时显得稍微有点乏力。
3.3.3 布特沃斯低通(高通)滤波器
截至频率位于距原点D0处的n阶布特沃斯低通滤波器(Butterworth Lowpass filter) 的传递函数定义为: H ( u , v ) = 1 1 + [ D ( u , v ) / D 0 ] 2 n H(u,v)=\frac{1}{1+[D(u,v)/D_0]^{2n}} H(u,v)=1+[D(u,v)/D0]2n1
截至频率位于距原点D0处的n阶布特沃斯高通滤波器(Butterworth Highpass filter) 的传递函数定义为: H ( u , v ) = 1 1 + [ D 0 / D ( u , v ) ] 2 n H(u,v)=\frac{1}{1+[D_0/D(u,v)]^{2n}} H(u,v)=1+[D0/D(u,v)]2n1
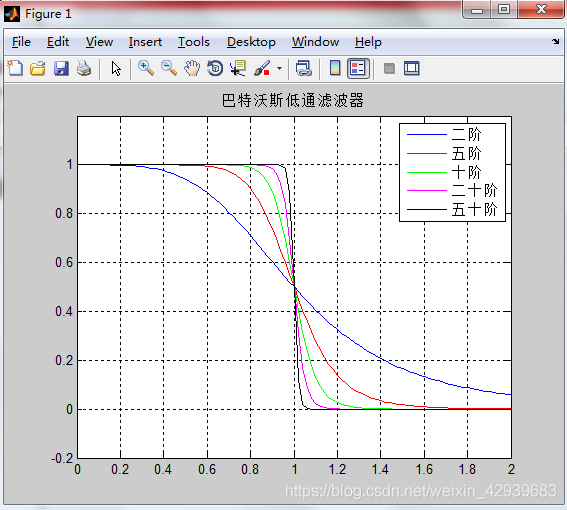
BLPF传递函数并没有像ILPF一样在通过频率和滤除频率之间给出明显的急剧不连续性，同时从上图可以看出n的值越小就越像高斯滤波器，随着n的值增大越来越像理想滤波器，并且截至频率点是当D(u,v)=D0时的点(即H(u,v)从其最大值下降为50%)。但是布特沃斯滤波器会随着n值增大振铃效果也逐步增大。
3.3.4 高频强调滤波
在空域处理中就有钝化模板、高提升滤波图像锐化技术，在频率域使用，由下式给出: g m a s k ( x , y ) = f ( x , y ) − f L P ( x , y ) g_{mask}(x,y)=f(x,y)-f_{LP}(x,y) gmask(x,y)=f(x,y)−fLP(x,y)与 f L P ( x , y ) = σ − 1 [ H L P ( u , v ) F ( u , v ) ] f_{LP}(x,y)=\sigma^{-1}[H_{LP}(u,v)F(u,v)] fLP(x,y)=σ−1[HLP(u,v)F(u,v)]式中，HLP(u,v)是一个低通滤波器，F(u,v)是f(x,y)的傅里叶变换。这里，fLP(x,y)是平滑后的图像，然后有： g ( x , y ) = f ( x , y ) + k ∗ g m a s k ( x , y ) g(x,y)=f(x,y)+k*g_{mask}(x,y) g(x,y)=f(x,y)+k∗gmask(x,y)该表达式定义了k=1时的钝化模板和k>1时的高提升滤波器。利用前面的结果，我们完全可以使用涉及低通滤波器的频率域计算来表达上式： g ( x , y ) = σ − 1 { [ 1 + k ∗ [ 1 − H L P ( u , v ) ] ] F ( u , v ) } g(x,y)=\sigma^{-1}\{[1+k*[1-H_{LP}(u,v)]]F(u,v)\} g(x,y)=σ−1{[1+k∗[1−HLP(u,v)]]F(u,v)}同样我们可以用高通滤波器来表达该结果: g ( x , y ) = σ − 1 { [ 1 + k ∗ H H P ( u , v ) ] F ( u , v ) } g(x,y)=\sigma^{-1}\{[1+k*H_{HP}(u,v)]F(u,v)\} g(x,y)=σ−1{[1+k∗HHP(u,v)]F(u,v)}方括号中的表达式称为高频强调滤波器。我们知道高通滤波器将直流项置0，因此会把滤波后的图像的平均灰度减小到0。高频强调滤波器不存在这一问题，因为高通滤波器上加了1.常数k给出了影响最终结果的高频的比例。高频强调滤波的通用公式为： g ( x , y ) = σ − 1 { [ k 1 + k 2 ∗ H H P ( u , v ) ] F ( u , v ) } g(x,y)=\sigma^{-1}\{[k_1+k_2*H_{HP}(u,v)]F(u,v)\} g(x,y)=σ−1{[k1+k2∗HHP(u,v)]F(u,v)}其中，k1≥0控制距原点的偏移量，k2≥0控制高频的贡献率。
4 MATLAB可视化频域处理
4.1 观察二维离散傅里叶变换
h = imread('jimei3.jpg');
f = im2double(rgb2gray(h)); %把图像变为灰度图像
F = fft2(f); %对图像进行傅里叶变换
FF = fftshift(F); %对图像频谱进行移动，使0频率点在中心
s=log(1 + abs(FF)); %获得傅里叶变换的幅度谱
phi = atan2(imag(F), real(F)); %获得傅里叶变换的相位谱
figure;
subplot(1,3,1),imshow(h),title('Original image');
subplot(1,3,2),imshow(s,[]),title('Fourier transform amplitude spectrum of image');
subplot(1,3,3),imshow(phi),title('Fourier transform phase spectrum of image');
效果如下
4.2 频率滤波
对于单幅图像我们先执行未使用0填充的滤波，
function H = lpfilter( type,M,N,D0,n )
%lpfilter lowpass filter
[U,V] = dftuv(M,N);
D = sqrt(U.^2 + V.^2);
switch type
case 'ideal'
H = double(D <= D0);
case 'btw'
if nargin ==4
n = 1;
end
H = 1./(1 + (D./DO).^(2*n));
case 'gaussian'
H = exp(-(D.^2)./(2*(D0^2)));
otherwise
error('Unknown filter type.')
end
function [U, V] = dftuv(M, N)
% DFTUV Computes meshgrid frequency matrices.
% Set up range of variables.
% 设置变量范围
u = 0 : (M - 1);
v = 0 : (N - 1);
% Compute the indices for use in meshgrid.
% 计算网格的索引，即将网络的原点转移到左上角，因为FFT计算时变换的原点在左上角。
idx = find(u > M / 2);
u(idx) = u(idx) - M;
idy = find(v - N / 2);
v(idy) = v(idy) - N;
% Compute the meshgrid arrays.
% 计算网格矩阵
[V, U] = meshgrid(v, u);
h = imread('jimei3.jpg');
f = im2double(rgb2gray(h));
[M,N] = size(f);
F = fft2(f);
sig = 10;
H = lpfilter('gaussian',M,N,sig);
G = H.*F;
g = real(ifft2(G));
subplot(1, 2, 1), imshow(h), title('Original image');
subplot(1, 2, 2), imshow(g,[]), title('Unfilled filtering');
效果如下
这里图像虽然变模糊了，但是注意垂直的边缘没有模糊，这里主要是因为处理是图像是非周期的，下面我们填充以后再进行滤波：
function PQ = paddedsize(AB, CD, PARAM)
if nargin == 1
PQ = 2*AB;
elseif nargin == 2 && -ischar(CD)
PQ = AB + CD - 1;
PQ = 2 * ceil(PQ / 2);
elseif nargin == 2
m = max(AB);
P = 2^nextpow2(2*m);
PQ = [P, P];
elseif (nargin == 3) && strcmp(PARAM, 'pwr2')
m = max([AB CD]);
P = 2^nextpow2(2*m);
PQ = [P, P];
else
error('Wrong number of inputs.')
end
PQ = paddedsize(size(f));
Fp = fft2(f,PQ(1),PQ(2));
Hp = lpfilter('gaussian',PQ(1),PQ(2),2*sig);
Gp = Hp.*Fp;
gp = ifft2(Gp);
gpc = gp(1:size(f,1),1:size(f,2));
figure;
subplot(1, 2, 1), imshow(h), title('Original image');
subplot(1, 2, 2), imshow(gpc,[]), title('Filled filtering');
效果如下
4.3 DFT滤波的基本步骤
前面的讨论可以概括为下面几个步骤，其中f是被滤波处理的图像，g为处理结果，同时假设滤波函数H与填充后的图像大小相等。
(1)用函数tofloat把输入图像变换为浮点图像：
[f,revertclass] = tofloat(f);
(2)用函数paddedsize获得填充参数：
PQ = paddedzsize(size(f));
(3)得到有填充的傅里叶变换：
F = fft2(f,PQ(1),PQ(2))；
(4)生成大小为PQ(1)×PQ(2)的滤波函数H:
H = lpfilter(type,PQ(1),PQ(2),variable);
(5)用滤波器乘以FFT变换:
G = H.*F
(6)获得G的逆FFT变换:
g = ifft2(G);
(7)修剪左上部矩形为原始大小:
g = g(1:size(f,1), 1:size(f,2));
总的来说：
预处理阶段包括确定图像大小，获得填充参数，以及生成滤波器函数。典型的后处理承担着修剪图像，并将之转换为输入类别的任务。
4.4 从空域滤波器获得频域滤波器
通常，当滤波器较小时，使用空域滤波要比频率滤波在计算时更有效，知道如何将空域滤波器转换为等同的频域滤波器的专门技术是很有用的，这一小节我们学习一下如何将空域滤波器转换为频域滤波器，同时进行一些比较。
g = imread('jimei2.jpg');
f = im2double(rgb2gray(g));
h = fspecial('sobel')
h =
1 2 1
0 0 0
-1 -2 -1
freqz2(h) %freqz2函数可以生成H的绝对值显示其三维透视图
subplot(1,2,1),imshow(f),title('Original image');
subplot(1,2,2),imshow(gs,[]),title('Filtering image');
接下来我们来对比频域下处理相同图片:
g = imread('jimei2.jpg');
f = im2double(rgb2gray(g));
h = fspecial('sobel');
PQ = paddedsize(size(f));
H = freqz2(h, PQ(1), PQ(2));
H1 = ifftshift(H); %这里我们需要对数据重排数据序列，使原点在频域矩形的左上角，freqz2默认原点在矩形中心。
gs = imfilter(f,h);
gf = dftfilt(f,H1);
figure;
subplot(1,2,1),imshow(gs,[]),title('Spatial processing image');
subplot(1,2,2),imshow(gf,[]),title('Image processed in frequency domain');
figure;
subplot(1, 2, 1), imshow(abs(H), [ ]), title('Abs of H');
subplot(1, 2, 2), imshow(abs(H1), [ ]), title('Abs of H1');
我们对比一下空域频域处理的结果：
我们可以看出来空域和频域处理效果是相当的，当然如果你将两张图片作差，最大差别也保持在10-6量级，已经很接近于0了。我们在看一下iffshift函数处理过的模板绝对值：
这里就能看出来变换后的滤波才符合DFT的周期性。
4.5 频域中直接生成滤波器
4.5.1 建立网格数组以实现频域滤波器
对于M-函数最主要的是：需要在频率矩形中计算任意点到规定点的距离函数，下面我们写一个称为dftuv的M-函数提供了距离计算以及其他类似应用所需要的网格数组。
function [U, V] = dftuv(M, N)
% Set up range of variables.
% 设置变量范围
u = 0 : (M - 1);
v = 0 : (N - 1);
% Compute the indices for use in meshgrid.
% 计算网格的索引，即将网络的原点转移到左上角，因为FFT计算时变换的原点在左上角。
idx = find(u > M / 2);
u(idx) = u(idx) - M;
idy = find(v > N / 2);
v(idy) = v(idy) - N;
% Compute the meshgrid arrays.
% 计算网格矩阵
[V, U] = meshgrid(v, u);
现在我们来看一下dftuv函数的作用：
>> [U,V] = dftuv(8,5);
>> DSQ = U.^2 + V.^2
DSQ =
0 1 4 4 1
1 2 5 5 2
4 5 8 8 5
9 10 13 13 10
16 17 20 20 17
9 10 13 13 10
4 5 8 8 5
1 2 5 5 2
>> fftshift(DSQ)
ans =
20 17 16 17 20
13 10 9 10 13
8 5 4 5 8
5 2 1 2 5
4 1 0 1 4
5 2 1 2 5
8 5 4 5 8
13 10 9 10 13
从这里我们能看出来函数处理过的以后矩阵左上角为0，距离最大位置在矩形中心，当我们用fftshift函数变换以后中心在(5,3)，数组关于这一点对称。
4.5.2 频域低通(平滑)滤波器
我们先使用理想滤波器，这里我用python来写一个手动理想滤波，将高频低频手动截取出来呈现给大家看：
import matplotlib.pyplot as plt
import numpy as np
if __name__=='__main__':
img = plt.imread('./raccoon.jpg')
plt.imshow(img, cmap=plt.cm.gray)
plt.axis('off')
plt.show()
img = img.mean(axis=-1)
img = np.fft.fft2(img)
img = np.fft.fftshift(img)
fourier = np.abs(img)
magnitude_spectrum = np.log(fourier)
plt.imshow(magnitude_spectrum.astype(np.uint8), cmap=plt.cm.gray)
plt.axis('off')
plt.show() # image after fourier transform
x,y = img.shape
lowF = np.zeros((x, y))
lowF = lowF.astype(np.complex128)
window_shape = (20, 20)
lowF[int(x / 2) - window_shape[0]:int(x / 2) + window_shape[0],int(y / 2) - window_shape[1]:int(y / 2) + window_shape[1]] = \
img[int(x / 2) - window_shape[0]:int(x / 2) + window_shape[0],int(y / 2) - window_shape[1]:int(y / 2) + window_shape[1]]
lowF_im = np.fft.ifft2(lowF)
lowF_im = np.abs(lowF_im)
lowF_im[lowF_im > 255] = 255
plt.imshow(lowF_im.astype(np.uint8), cmap='gray')
plt.axis('off')
plt.show()
highF = np.zeros((x, y))
highF = highF.astype(np.complex128)
window_shape = (370, 370)
highF[0:window_shape[0], :] = img[0:window_shape[0], :]
highF[x - window_shape[0]:x, :] = img[x - window_shape[0]:x, :]
highF[:, 0:window_shape[1]] = img[:, 0:window_shape[1]]
highF[:, y - window_shape[1]:y] = img[:, y - window_shape[1]:y]
highF_im = np.fft.ifft2(highF)
highF_im = np.abs(highF_im)
highF_im[highF_im > 255] = 255
plt.imshow(highF_im.astype(np.uint8), cmap='gray')
plt.axis('off')
plt.show()
下面4张图分别是原图，傅里叶谱，理想低通滤波结果，理想高通滤波结果。
这里因为是我手动把变换后矩阵中的一部分拿出来，所以再变换回来的低通滤波是没有产生“振铃效果”的。
然后我们再实践一下高斯低通滤波：
>> r = imread('raccoon.jpg');
>> f = im2double(rgb2gray(r));
>> PQ = paddedsize(size(f));
>> [U,V] = dftuv(PQ(1),PQ(2));
>> D = hypot(U,V);
>> DO = 0.05*PQ(2);
>> F = fft2(f, PQ(1), PQ(2));
>> H = exp(-(D.^2)/(2*(DO^2)));
>> g = dftfilt(f,H);
>> figure;
>> subplot(2, 2, 1), imshow(r), title('Original Image');
>> subplot(2, 2, 2), imshow(fftshift(H),[]), title('Gaussian Lowpass filter');
>> subplot(2, 2, 3), imshow(log(1 + abs(fftshift(F))),[]), title('Logarithmically enhanced Fourier transform');
>> subplot(2, 2, 4), imshow(g,[]), title('Image filtered by Gauss low pass filter');
4.5.3 线框及表面绘制
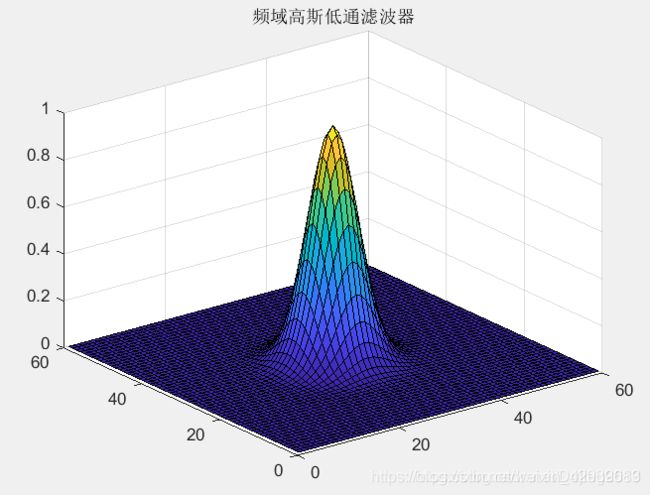
我们不断在学习不同种类的滤波器，有时我们想要将滤波器可视化出来，这样能让实验者对该滤波器有一个更清晰的认识，这一小节就学习一下3D线框及表面的绘制，我们要用到的是matlab中的mesh函数。
>> g = lpfilter('gaussian',500, 500, 50);
>> H = fftshift(g);
>>> mesh(double(H(1:10:500,1:10:500)));
>> axis tight
我们可以把绘图的线条变为黑色，消除轴和栅格：
>> colormap([0 0 0])
>> axis off
>> grid off
同时我们可以调整观察点，以方位角和仰角为参数。
view(-25, 0)
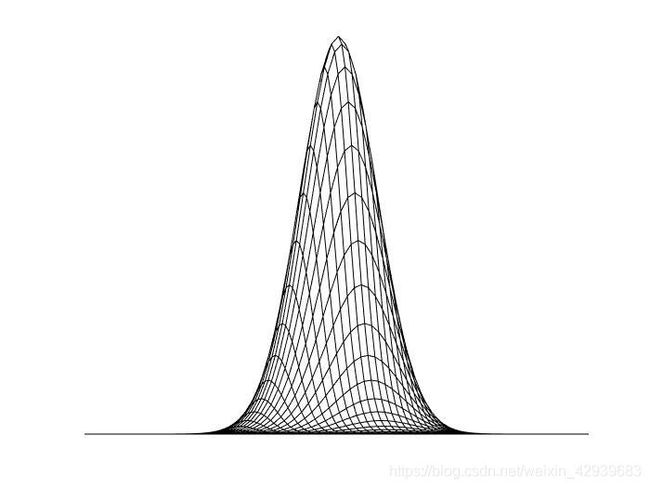如果要绘制含有两个变量的解析函数，就用meshgrid产生坐标值，并从这些坐标值中产生将在mesh或surf中使用的离散(抽样)矩阵。例如，绘制函数 f ( x , y ) = x e ( − x 2 − y 2 ) f(x,y)=xe^{(-x^2-y^2)} f(x,y)=xe(−x2−y2)
>> [Y, X] = meshgrid(-2:0.1:2, -2:0.1:2);
>> Z = X.*exp(-X.^2 - Y.^2);
>> surf(Z);
>> axis tight;
4.5.4 高通(锐化)频域滤波器
在之前我就已经用python实现了一个理想的高通滤波器，这里我们只实现一个简单的高斯高通滤波器实验一下：
>> w = imread('raccoon.jpg');
>> f = im2double(rgb2gray(w));
>> PQ = paddedsize(size(f));
>> [U,V] = dftuv(PQ(1), PQ(2));
>> DO = 0.05&PQ(1);
>> H = hpfilter('gaussian',PQ(1), PQ(2), DO);
>> g = dftfilt(f, H);
>> figure;
>> subplot(1, 2, 1), imshow(w), title('Original Image');
>> subplot(1, 2, 2), imshow(g,[]), title('Gauss high pass filtered image');
下面我们再来看高频强调滤波:
>> HBW = hpfilter('btw', PQ(1),PQ(2), D0, 2);
>> H = 0.5 + 2*HBW;
>> gbw = dftfilt(f,HBW,'fltpoint');
>> gbw = gscale(gbw);
>> ghf = dftfilt(f,H,'fltpoint');
>> ghf = gscale(ghf);
>> ghe = histeq(ghf, 256);
>> subplot(2,2,1),imshow(w),title('Original Image');
>> subplot(2, 2, 2), imshow(gbw,[]), title('The result of filtering by butworth filter');
>> subplot(2, 2, 3), imshow(ghf,[]), title('Results of high frequency emphasis');
>> subplot(2, 2, 4), imshow(ghe,[]), title('Histogram equalization results after high frequency emphasis');
由结果我们可以看出来，光有高频强调滤波加强后，灰度值范围还是狭窄的，所以将高频强调滤波和直方图均衡结合起来得到的结果要好于单独使用任何一种方法。