彩色图像处理之色彩学基础
彩色图像处理 – 色彩学基础
什么是色彩
// 神说、要有光、就有了光。 וַיֹּאמֶר אֱלֹהִים, יְהִי אוֹר; וַיְהִי-אוֹר
// —— 旧约·创世记
const float c = 299792.458所谓色彩本质是光。
或者更精确来说,色彩是外界在一定波长范围内(大约400nm-700nm)的具有不同频谱的光经过人体的光学感受器件(视网膜)后通过在神经中传播的电信号在大脑相关区域印下的某种主观感受。
人类对于色彩的理解是一种仍然未被完全了解的生理和心理现象。但是人们通过各种实验得到了一些关于颜色的性质的结果并形成了理论,这就是色彩学(color theory)。色彩学主要关心的是我们对于不同颜色的主观感受以及颜色之间的组合方式带来的效果。
1666年,艾萨克·牛顿发现了光的色散现象,所谓认为的纯白的太阳光实际上是各个频段(主观上看就是各个颜色)的光的混合的结果。光的特性是色彩学的基础和核心,研究光的物理性质以及人类视觉感受器的形式可以揭示出色彩的某些规律。

人类视觉系统

如图所示,人类的光学器件是眼球,而真正起到感受器作用的则是视网膜上的视锥细胞和视杆细胞。 他们的名字就来源于其形状。两者作用不同,视杆细胞主司暗视觉,即在夜晚光线不明朗的时候,视杆细胞更能起作用,而在日光下往往感受不敏锐;而视锥细胞主司明视觉,以及颜色视觉,我们之所以能够分辨不同的颜色都是有赖于视锥细胞。在视网膜的大部分区域,视杆细胞远远多于视锥细胞。只有在黄斑的中央凹位置(图中标注fovea的位置),才只有视锥细胞,因此这里自然是我们视力最敏锐的区域。(一个不难推断但是颇为有趣的现象就是,在昼伏夜出的动物(比如老鼠)的视网膜里面,视杆细胞比较多;相反白昼出没的动物(如鸡)则视锥细胞多些。)
人类管颜色的视锥细胞分为三种:可以习惯性的称为红色视锥细胞,绿色视锥细胞,以及蓝色视锥细胞。这是因为他们具有不同的对光吸收曲线,之所以用以上三种颜色命名,是因为这三种视锥细胞在这大概三种颜色的位置呈现出一个吸收的高峰。如下图所示:

这些曲线可以消除有些人的误解:即认为红绿蓝三种颜色指的是一个确定的波长的值,而三种视锥细胞在相应的波长上又一个脉冲相应。其实并非如此,颜色实际上都是渐变的,不存在一个固定波长的红色等。当然,为了标准化起见,CIE(Commission Internationale de L’Eclairage)国际照明委员会在1931年还是规定了下面特定波长的三原色:
蓝色:435.8 nm
绿色:546.1 nm
红色:700 nm
三原色理论
由于人类视觉系统的特点,我们把光的红,绿,蓝称为三原色(primary colors)。历史上对于用哪几种颜色作为原色才能更好的表征人类眼睛对于颜色的感受有过争论,其中,托马斯杨(对就是那个大名鼎鼎的物理学家,双缝干涉的那个,还有杨氏模量,都是他的成果)认为应该是红绿紫,而麦克斯韦(就是麦克斯韦方程组的那个麦克斯韦…那时候的科学家真滴是全才…)认为应该是红绿蓝。当然从现代的角度来看,实际上并不存在三种确定的颜色,如上所述,每种颜色的视锥细胞对于不同波长其实都有一定的较为宽泛的感受范围。
根据三原色理论,光的三原色就是红绿蓝,对它们进行相加混合后可以得到二次色(又称间色)深红青黄,最终混合产生白色光。(如图所示)而颜料之间的三原色不同,由于颜料的色彩是由于它反射的光决定的,因此颜料的原色定义为:吸收光的某种原色而反射出来的另外两种原色,因此,颜料的原色是深红,青,黄,即cyan, magenta, yellow,看到这个首字母应该可以猜到了,这就是CMYK中的CMY。颜料的混合得到的间色为红绿蓝,完全混合得到黑色。
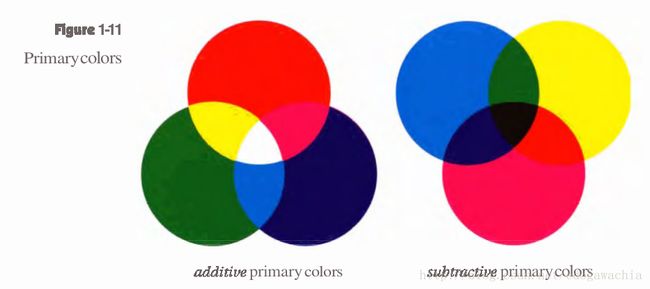
格拉斯曼颜色定律(Grassmann’s laws)
格拉斯曼定律描述了不同颜色混合的经验规律,如下:
- 第一定律:Two colored lights appear different if they differ in either dominant wavelength, luminance or purity.
实际上就是说明了颜色的三个要素,主波长就是色调,luminance是亮度,以及purity,纯度,应该就是饱和度的类似提法。
- 第二定律:The appearance of a mixture light made from two components changes if either component changes.
说明混合的颜色中的任何一个颜色改变都会影响混合结果。
- 第三定律:There are lights with different spectral power distributions but appear identical.
这就是同色异谱现象,这样的同色在混合的时候可以看做同样的颜色,得到的混合结果也是一样的。
- 第四定律:The intensity of a mixture of lights is the sum of the intensities of the components.
这个反映了颜色混合的相加的关系。
格拉斯曼颜色定律表明了人类对于颜色的视觉感受近似是线性的。下面这个图被格拉斯曼用来解释他的第一定律,色谱用圆环排列。感觉基本上有了色度图的雏形。
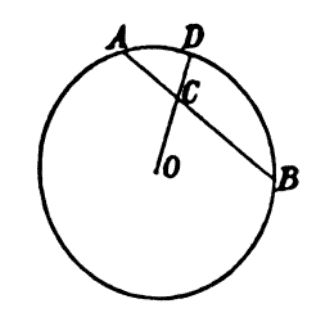
光谱的色度特性实验 (The Colorimetric Properties of the Spectrum)
为了定量的研究三原色是如何线性的构造出所有的颜色的,科学家们做了如下实验:

由于可见光的范围是有限的,因此可以对于每个波长(有间隔的取值)的可见光都进行一次实验。实验方法如上图所示:首先,放置两块白板,中间水平隔开,分为上下两部分,上方是我们待测的颜色,下面是红绿蓝三原色,上下同时照射到后面的白板上,前面的白板开一孔,测试者从孔中观测上下两种颜色是否一致。如果不一致,就调节三原色的配比,知道人无法分辨两种颜色为止。然后记录下这个波段的光对应的三原色的系数。
当所有颜色都做完一遍之后,可以画出如下曲线:

发现其中有一部分红色需要取负值,这代表着,上面是待测波长的光,下面是三原色,无论怎么调节都调不出相等,所以需要把红光加在上面,然后下面用另两个颜色,这样就得到了带负值的曲线。
有了这个曲线,我们发现,对于每种颜色我们都能用三原色的系数值表示出来他们,所以每个颜色可以用一个三维向量来表征,可是这样的话,没法用一个平面直观地表示出来,于是我们利用
其中大写的RGB表示上面曲线的三原色的系数值。实际上是将三个系数归一化了,这样以来,只需要两个数,比如r和g,就可以表示各种颜色了,当然这样的表示体现不出亮度,只能体现出色度,即色调和饱和度。
把归一化后的r和g当做两个维度,作图可以得到:
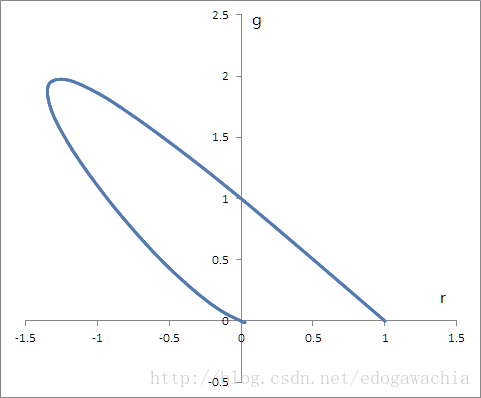
为了避免出现负数,进行坐标变换得到:

填上颜色,就可以得到CIE色度图

可以看到,在这个舌形色度图内部的颜色就是所有的颜色,边缘的点就是各种谱色,对应这不同波长的纯色。而中间的则为混合色。我们看到,最中间的位置叫做等能量点,就是说三原色的能量相等,因此是白色。就是白光的CIE标准。下图为对CIE色度图的分析:
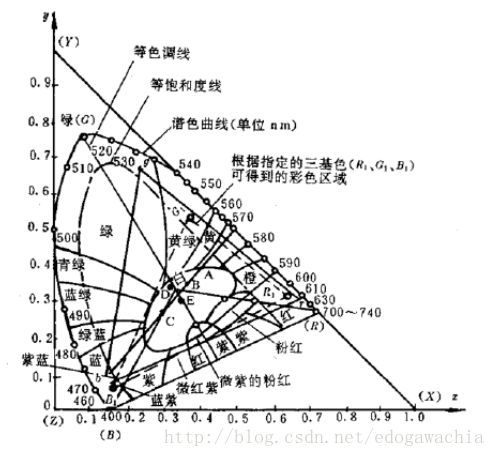
可以看出,沿着白色和某一已知颜色点的连线是等色调线,也就是说,这些颜色有一样的色调,而沿着这条线向着白色的中心走的时候,饱和度逐渐变弱,所以以这些等色调线为法线的曲线就是等饱和度线。而作为颜色的三要素的:明度,色调,饱和度中的明度(luminance)则无法从这张图中得到。
如果我们在里面选择三个点作为三原色,然后用加法表示其他颜色的话,显然,所得到的结果应在这三点围成的三角形内,包括边界。如图:
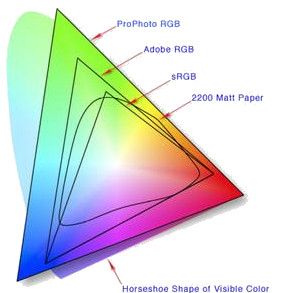
所以不管选择哪三个点,都没法完全用加法的方式表示出所有的visible color,这是由于色度图的形状决定的。
正好这个图里也标出了一个不规则区域,这是打印的颜色域,也不可能覆盖所有的可见光,很多时候在网上买东西遇到有色差的问题,可能也是由于这个原因。
reference:
数字图像处理 第三版 Gonzalez
Real World Color Management, Second Edition , Bruce Fraser
https://en.wikipedia.org/wiki/Grassmann%27s_laws_(color_science)
https://en.wikipedia.org/wiki/Color_theory
https://en.wikipedia.org/wiki/CIE_1931_color_space
https://mp.weixin.qq.com/s?__biz=MzIwNDQwNTM5NQ==&mid=2247492519&idx=1&sn=895aba2aee3e0fad3e8bb30cc5e3429a&chksm=96c20c5ba1b5854d58cb24e6e6d1eedcb1674d858caea1adbdefcf49287b09490fd7b1b97c5f&scene=21##
(未完待续:next :彩色模型与颜色空间)
* 本文只限于针对彩色图像处理领域相关的工作,讲解基本的色彩理论,如果想要深入了解的读者,小编推荐一个weixin公众号,叫做【颜色的前世今生】,里面的文章很不错,内容也很丰富,这篇文章在色度图的相关内容即参考了公众号中的一篇文章的相关内容。
2018/01/26 20:00 pm
人生是个含泪的微笑。 —— 欧亨利