计算机视觉编程——多视图几何

多视图几何

多视图几何是利用在不同视点所拍摄的图像间的关系，来研究照相机之间或者特征之间关系的一门学科。图像的特征通常就是兴趣点。

1 外极几何

如果一个场景的两个视图以及视图中的对应图像点，那么根据照相机间的空间相对位置关系、照相机的性质以及三维场景点的位置，可以得到对这些图像点的几何约束关系，即外极几何。

1.1 一个简单的数据集

使用下面的程序加载两个图像、三个视图中的所有图像特征点、对应不同视图图像点重建后的三维点以及照相机参数矩阵。

import my_camera

im1 = array(Image.open('001.jpg'))
im1 = array(Image.open('002.jpg'))

points2D = [loadtxt('2D/00' + str(i + 1) + '.corners').T for i in range(3)]

points3D = loadtxt('3D/p3d').T

corr = genfromtxt('2D/nview-corners', dtype = 'int', missing = '*')

P = [my_camera.Camera(loadtxt('2D/00' + str(i + 1) + '.P')) for i in range(3)]

使用loadtxt()函数读取文本文件到NumPy数组中，因为并不是所有的点都可见，或都能够成功匹配到所有的视图，所以对应数据里包含了缺失的数据。genfromtxt()函数通过将缺失的数值填充为-1来解决这个问题。

将上述代码保存到load_vggdata.py，然后使用命令excefile()可以运行该脚本，从而获取数据：

execfile('load_vggdata.py')

结果报错：NameError: name ‘execfile’ is not defined

这是由于execfile()在python3中已被废除，可以使用代替函数： exec(open(filename).read())来完成。

下面来可视化这些数据，将三维的点投影到一个视图上，然后和观测到的图像点比较：

X = vstack((points3D, ones(points3D.shape[1])))
x = P[0].project(X)

figure()
imshow(im1)
plot(points2D[0][0], points2D[0][1], '*')
axis('off')

figure()
imshow(im1)
plot(x[0], x[1], 'r.')
axis('off')

show()

图1 图像点与三维投影点

上边的代码绘制出第一个视图以及该视图中的图像点。仔细观察发现第二幅图比第一幅图多一些点，这些多出来的点是从视图2和视图3重建出来的，而不是在视图1中。

1.2 用Matplotlib绘制三维数据

为了可视化三维重建结果，需要绘制出三维图像。Matplotlib中的mplot3d工具包可以方便地绘制出三维点、线、等轮廓线、表面以及其他基本图形组件，还可以通过图像窗口控件实现三维旋转和缩放。

可以通过在axes对象中加上projection=“3d”关键字实现三维绘图，如下：

from mpl_toolkits.mplot3d import axes3d

fig = figure()
ax = fig.gca(projection = "3d")

X, Y, Z = axes3d.get_test_data(0.25)

ax.plot(X.flatten(), Y.flatten(), Z.flatten(), 'o')

show()

get_test_data()函数在x，y空间按照设定的空间间隔参数来产生均匀的采样点。压平这些网格会产生三列数据点，然后可以将其输入plot()函数，就可以在立体表面画出这些三维点。

图2 立体表面的三维点

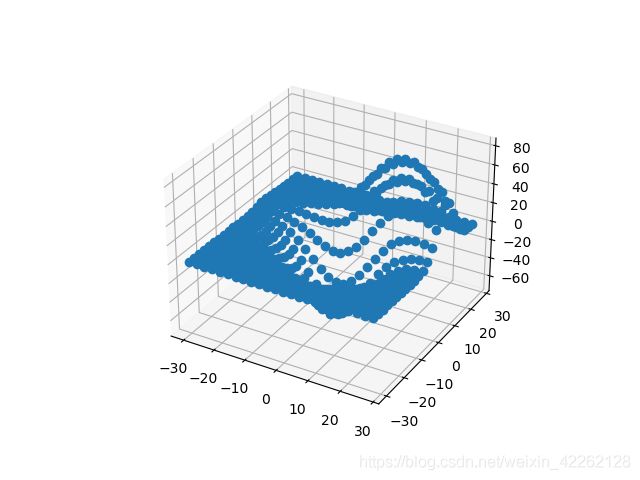
通过画出Merton样本数据来观察三维点的效果：

fig = figure()
ax = fig.gca(projection = "3d")
ax.plot(points3D[0], points3D[1], points3D[2], 'k.')

show()

图3 建筑墙体和屋顶上的三维点

1.3 计算F：八点法

八点法是通过对应点来计算基础矩阵的算法。

下面的代码写入八点法中最小化||Af||的函数：

def compute_fundamental(x1, x2):
	n = x1.shape[1]
	
	if x2.shape[1] != n:
		raise ValueError("Number of points don't match.")
		
	A = zeros((n, 9))
	
	for i in range(n):
		A[i] = [x1[0, i] * x2[0, i], x1[0, i] * x2[1, i], x1[0, i] * x2[2, i],
				x1[1, i] * x2[0, i], x1[1, i] * x2[1, i], x1[1, i] * x2[2, i],
				x1[2, i] * x2[0, i], x1[2, i] * x2[q, i], x1[2, i] * x2[0, i]]

	U, S, V = linalg.svd(A)
	F = V[-1].reshape(3, 3)
	
	U, S, V = linalg.svd(F)
	S[2] = 0
	F = dot(U, dot(diag(S), V))
	
	return F

通常使用SVD算法来计算最小二乘解。由于上面算法得出的解可能秩不为2，所以通过将最后一个奇异值置为0来得到秩最接近2的基础矩阵。

1.4 外极点和外极线

如果要获得一幅图像的外极点，只需要将F转置后输入下述函数：

def compute_epipole(F):
	U, S, V = linalg.svd(F)
	e = V[-1]
	
	return e / e[2]

def plot_epipolar_line(im, F, x, epipole = None, show_epipole = True):
	m, n = im.shape[:2]
	line = dot(F, x)
	
	t = linspace(0, n, 100)
	lt = array([(line[2] + line[0] * tt) / (-line[1]) for tt in t])
	
	ndx = (lt >= 0) & (lt < m)
	plot(t[ndx], lt[ndx], linewidth = 2)
	
	if show_epipole:
		if epipole is None:
			epipole = compute_epipole(F)
		plot(epipole[0] / epipole[2], epipole[1] / epipole[2], 'r*')

上面的函数将x轴的范围作为直线的参数，因此直线超出图像边界的部分会被截断。如果show_epipole为真，外极点也会被画出来（如果输入参数没有外极点，则外极点会在程序中计算出来）。
可以在之前样本数据集的前两个视图上运行这两个函数：

ndx = (corr[:, 0] >= 0) & (corr[:, 1] >= 0)

x1 = points2D[0][:, corr[ndx, 0]]
x1 = vstack((x1, ones(x1.shape[1])))

x2 = points2D[1][:, corr[ndx, 1]]
x2 = vstack((x2, ones(x2.shape[1])))

F = sfm.compute_fundamental(x1, x2)

e = sfm.compute_epipole(F)

figure()
imshow(im1)

for i in range(5):
	sfm.plot_epipolar_line(im1, F, x2[:, i], e, False)
axis('off')

figure()
imshow(im2)

for i in range(5):
	plot(x2[0, i], x2[1, i], 'o')
axis('off')

show()

首先选择两幅图像的对应点，然后将他们转换为齐次坐标。然后画出了对应匹配点。在下图中用不同颜色将点和相应的外极线对应起来。

图4 数据视图中的5个外极点

2 照相机和三维结构的计算

2.1 三角剖分

给定照相机参数模型，图像点可以通过三角剖分来恢复出这些点的三维位置。基本算法思想如下：
对于两个照相机P1，P2的视图，三维实物点X的投影点x1和x2，照相机方程定义了下列关系：

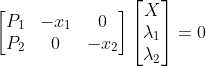
由于图像噪声、照相机参数误差和其他系统误差，上面的方程可能没有精确解。需要用到SVD算法来得到三维点的最小二乘估值。

下面的函数用于计算一个点对的最小二乘三角剖分：

def triangulate_points(x1, x2, P1, P2)：
	M = zeros((6, 6))
	M[:3, :4] = P1
	M[3:, :4] = P2
	M[:3, 4] = -x1
	M[3:, 5] = -x2
	
	U, S, V = linalg.svd(M)
	X = V[-1, :4]
	
	return X / X[3]

最后一个特征向量的前4个值就是齐次坐标系下的对应三维坐标，可以增加下面的函数来实现多个点的三角剖分：

def triangulate(x1, x2, P1, P2):
	n = x1.shape[1]
	if x2.shape[1] != n:
		raise ValueError("Number of points don't match.")
	
	X = [triangulate_points(x1[:, i], x2[:, i], P1, P2) for i in range(n)]
	
	return array(X).T

这个函数的输入是两个图像点数组，输出为一个三维坐标数组。

可以利用下面的代码来实现三角剖分：

ndx = (corr[:, 0] >= 0) & (corr[:, 1] >= 0)

x1 = points2D[0][:, corr[ndx, 0]]
x1 = vstack((x1, ones(x1.shape[1])))
x2 = points2D[1][:, corr[ndx, 1]]
x2 = vstack((x2, ones(x2.shape[1])))

Xtrue = points3D[:, ndx]
Xtrue = vstack((Xtrue, ones(Xtrue.shape[1])))

Xest = sfm.triangulate(x1, x2, P[0].P, P[1],P)
print(Xest[:, :3])
print(Xtrue[:, :3])

from mpl_toolkits.mplot3d import axes3d

fig = figure()
ax = fig.gca(projection = '3d')
ax.plot(Xest[0], Xest[1], Xest[2], 'ko')
ax.plot(Xtrue[0], Xtrue[1], Xtrue[2], 'r.')

axis('equal')

show()

上面的代码首先利用前两个视图的信息来对三维点进行三角剖分，然后把前三个图像点的齐次坐标输出到控制台，最后绘制出灰度的最接近三维图像点。输出到控制台的信息如下：
[[ 1.03743725 1.56125273 1.40720017]
[-0.57574987 -0.55504127 -0.46523952]
[ 3.44173797 3.44249282 7.53176488]
[ 1. 1. 1. ]]
[[ 1.0378863 1.5606923 1.4071907 ]
[-0.54627892 -0.5211711 -0.46371818]
[ 3.4601538 3.4636809 7.5323397 ]
[ 1. 1. 1. ]]
算法估计出的三维图像点和实际图像点很接近。

图5 使用照相机矩阵和点的对应关系三角剖分数据点

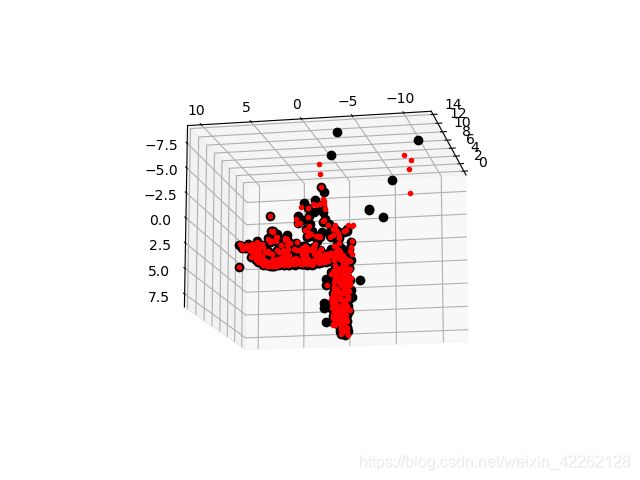
2.2 由三维点计算照相机矩阵

如果已经知道了一些三维点及其图像投影，可以使用直接线性变换的方法来计算照相机矩阵P。本质上这也是三角剖分方法的逆问题，也称照相机反切法。

相应代码如下：

def compute_P(x, X):
	n = x.shape[1]
	 if X.shape[1] != n:
		 raise ValueError("Number of points don't match.")
		 
	M = zeros((3 * n, 12 + n))
	for i in range(n):
		M[3 * i, 0: 4] = X[:, i]
		M[3 * i + 1, 4: 8] = X[:, i]
		M[3 * i + 2, 8: 12] = X[:, i]
		M[3 * i: 3 * i + 3, i + 12] = -x[:, i]
		
	U, S, V = linalg.svd(M)
		
	return V[-1, :12].reshape((3, 4))

该函数的输入参数为图像点和三维点，构造出上述所示的M矩阵。最后一个特征向量的前12个元素是照相机矩阵的元素，经过重新排列成矩阵形状后返回。

下面，在样本数据集上测试算法的性能。

corr = corr[:, 0]
ndx3D = where(corr >= 0)[0]
ndx2D = corr[ndx3D]

x = points2D[0][:, ndx2D]
x = vstack((x, ones(x.shape[1])))
X = points3D[:, ndx3D]
X = vstack((X, ones(X.shape[1])))

Pest = my_camera.Camera(sfm.compute_P(x, X))

print(Pest.P / Pest.P[2, 3])
print(P[0].P / P[0].P[2, 3])

xest = Pest.project(X)

figure()
imshow(im1)
plot(x[0], x[1], 'bo')
plot(xest[0], xest[1], 'r.')
axis('off')

show()

上面的代码选出第一个视图中的一些可见点，将它们转换为齐次坐标表示，然后估计照相机矩阵。为了检查照相机矩阵的正确性，将他们归一化的格式（除以最有一个元素）打印到控制台。输出如下所示：
[[ 1.06520794e+00 -5.23431275e+01 2.06902749e+01 5.08729305e+02]
[-5.05773115e+01 -1.33243276e+01 -1.47388537e+01 4.79178838e+02]
[ 3.05121915e-03 -3.19264684e-02 -3.43703738e-02 1.00000000e+00]]
[[ 1.06774679e+00 -5.23448212e+01 2.06926980e+01 5.08764487e+02]
[-5.05834364e+01 -1.33201976e+01 -1.47406641e+01 4.79228998e+02]
[ 3.06792659e-03 -3.19008054e-02 -3.43665129e-02 1.00000000e+00]]

图6 使用估计出的照相机矩阵计算视图1中的投影点
可以看出估计出的照相机矩阵和数据集计算出的照相机矩阵，它们的元素几乎完全相同。最后使用估计出的照相机矩阵投影这些三维点，然后绘制出投影后的结果，如上图所示，真实点用圆圈表示，估计出的照相机投影点用点表示。

2.3 由基础矩阵计算照相机矩阵

在两个视图场景中，照相机矩阵可以由基础矩阵恢复出来。研究分为两类：未标定的情况和已标定的情况。

2.3.1 投影重建

在没有任何照相机内参数知识的情况下，照相机矩阵只能通过射影变换恢复出来。也就是说，如果利用照相机信息来重建三维点，那么该重建只能由射影变换计算出来。（在这里不考虑角度和距离）
具体代码如下：

def skew(a):
	return array([[0, -a[2], a[1]], [a[2], 0, -a[0]], [-a[1], a[0], 0]])
	
def compute_P_from_fundamental(F):
	e = compute_epipole(F.T)
	Te = skew(e)
	
	return vstack((dot(Te, F.T).T, e)).T

2.3.1 度量重建

在已标定的情况下，重建会保持欧式空间中的一些度量特性（除了全局的尺度参数）。从本质矩阵恢复出的照相机矩阵中存在度量关系，但有四个可能解。因为只有一个解产生位于两个照相机前的场景，所以可以轻松选出。
具体代码如下：

def compute_P_from_essential(E):
	U, S, V = svd(E)
	
	if det(dot(U, V)) < 0:
		V = -V
	
	E = dot(U, dot(diag([1, 1, 0]), V))
	
	Z = skew([0, 0, -1])
	W = array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])
	
	P2 = [vstack((dot(U, dot(W, V)).T, U[:, 2])).T,
		  vstack((dot(U, dot(W, V)).T, -U[:, 2])).T,
		  vstack((dot(U, dot(W.T, V)).T, U[:, 2])).T,
		  vstack((dot(U, dot(W.T, V)).T, -U[:, 2])).T]
		  
	return P2

3 多视图重建

由于照相机的运动给我们提供了三维结构，所以这样计算三维重建的方法通常称为SfM。

假设照相机已经标定，计算重建可以分为下面4个步骤：

1. 检测特征点，然后在两幅图之间匹配
2. 由匹配计算基础矩阵
3. 由基础矩阵计算照相机矩阵
4. 三角剖分这些三维点

3.1 稳健估计基础矩阵

这部分类似于稳健计算单应性矩阵，当存在噪声和不正确的匹配时，需要估计基础矩阵。使用RANSAC方法并结合八点法来完成。

class RansacModel(object):
	def __init__(self, debug = False):
		self.debug = debug
		
	def fit(self, data):
		data = data.T
		x1 = data[:3, :8]
		x2 = data[3:, :8]
		
		F = compute_fundamental_normalized(x1, x2)
		
		return F
		
	def get_error(self, data, F):
		data = data.T
		x1 = data[:3]
		x2 = data[3:]
		
		Fx1 = dot(F, x1)
		Fx2 = dot(F, x2)
		denom = Fx1[0] ** 2 + Fx[1] ** 2 + Fx2[0] ** 2 + Fx2[1] ** 2
		
		err = (diag(dot(x1.T, dot(F, x2)))) ** 2 / denom
		
		return err

def compute_fundamental_normalized(x1, x2):
	n = x1.shape[1]
	if x2.shape[1] != n:
		raise ValueError("Number of points don't match.")

	x1 = x1 / x1[2]
	mean_1 = mean(x1[:2], axis = 1)
	S1 = sqrt(2) / std(x1[:2])
	T1 = array([[S1, 0, -S1 * mean_1[0]], [0, S1, -S1 * mean_1[1]], [0, 0, 1]])
	x1 = dot(T1, x1)
	
	x2 = x2 / x2[2]
	mean_2 = mean(x2[:2], axis = 1)
	S2 = sqrt(2) / std(x2[:2])
	T2 = array([[S2, 0, -S2 * mean_2[0]], [0, S2, -S2 * mean_2[1]], [0, 0, 1]])
	x2 = dot(T2, x2)
	
	F = compute_fundamental(x1, x2)
	
	F = dot(T1.T, dot(F, T2))
	
	return F / F[2, 2]

def F_from_ransac(x1, x2, model, maxiter = 5000, match_theshold = 1e-6):
	import ransac
	
	data = vstack((x1, x2))
	
	F, ransac_data = ransac.ransac(data.T, model, 8, maxiter, match_theshold, 20, return_all = True)
	
	return F, ransac_data['inliers']

这里返回最佳基础矩阵F，以及正确点的索引，可以知道那些匹配和F矩阵是一致的。与单应性矩阵估计相比，增加了默认的最大迭代次数，改变了匹配的阈值。

3.2 三维重建示例

在接下来的处理中，将该示例的处理代码分成若干块，使得代码更容易理解。首先，提取、匹配特征，然后估计基础矩阵和照相机矩阵：

K = array([[2394, 0, 932], [0, 2398, 628], [0, 0, 1]])

im1 = array(Image.open('alcatraz1.jpg'))
my_sift.process_image('alcatraz1.jpg', 'im1.sift')
l1, d1 = my_sift.read_features_from_file('im1.sift')

im2 = array(Image.open('alcatraz2.jpg'))
my_sift.process_image('alcatraz2.jpg', 'im2.sift')
l2, d2 = my_sift.read_features_from_file('im2.sift')

matches = my_sift.match_twosided(d1, d2)
ndx = matches.nonzero()[0]

x1 = my_homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = my_homography.make_homog(l2[ndx2, :2].T)

x1n = dot(inv(K), x1)
x2n = dot(inv(K), x2)

model = sfm.RansacModel()
E, inliers = sfm.F_from_ransac(x1n, x2n, model)

P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 0, 1]])
P2 = sfm.compute_P_from_essential(E)

在获得了标定矩阵后，对矩阵K进行硬编码。使用K的逆矩阵来对其进行归一化，并使用归一化的八点算法来运行Ransac估计，返回一个本质矩阵并保存正确匹配点的索引。从本质矩阵出发，可以计算出第二个照相机矩阵的四个可能解。

从照相机矩阵的列表中，挑选出经过三角剖分后，在两个照相机前郡含有场景点的照相机矩阵：

ind = 0
maxres = 0
for i in range(4):
	X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2[i])
	d1 = dot(P1, X)[2]
	d2 = dot(P2[i], X)[2]
	
	if sum(d1 > 0) + sum(d2 > 0) > maxres:
		maxres = sum(d1 > 0) + sum(d2 > 0)
		ind = i
		infront = (d1 > 0) & (d2 > 0)
		
	X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2[ind])
	X = X[:, infront]

循环遍历这四个解，每次对对应于正确点的三维点进行三角剖分。将三角剖分后的图像投影回图像后，深度的符号由每个图像点的第三个数值给出。我们保存了正向最大深度的索引；对于和最优解一致的点，用相应的布尔变量保存了信息，这样可以取出真正在照相机前面的点。因为所有估计中都存在噪声和误差，所以即便使用正确的照相机矩阵，也存在一些点仍位于某个照相机后面的风险。首先获得正确的解，然后对这些正确的点进行三角剖分，最后保留位于照相机前方的点。

现在可以绘制出该三维重建：

cam1 = my_camera.Camera(P1)
cam2 = my_camera.Camera(P2)

x1p = cam1.project(X)
x2p = cam2.project(X)

x1p = dot(K, x1p)
x2p = dot(K, x2p)

figure()
imshow(im1)
gray()
plot(x1p[0], x1p[1], 'o')
plot(x1[0], x1[1], 'r.')
axis('off')

figure()
imshow(im2)
gray()
plot(x2p[0], x2p[1], 'o')
plot(x2[0], x2[1], 'r.')
axis('off')

show()

将这些三维点投影后，可以通过乘以标定矩阵的方式来弥补初始归一化对点的影响。
程序在运行中出现一个问题：

图7 三维重建中遇到的问题
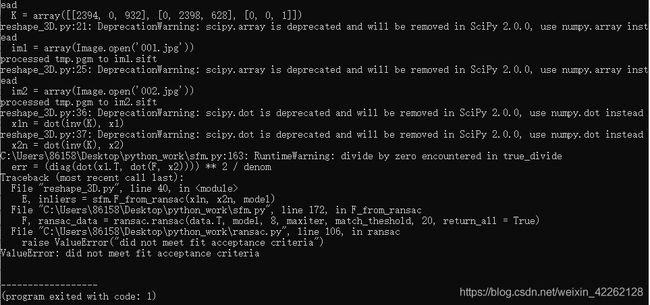
最后得到的结果如下图所示：
图8 使用图像匹配从一对图像中计算三维重建
从图中可以看到，二次投影后的点和原始特征位置不完全匹配，但是相当接近。可以进一步调整照相机矩阵来提高重建和二次投影的性能。

4 立体图像

一个多视图成像的特殊例子是立体视觉，即使用两台只有水平偏移的照相机观测同一场景。当照相机的位置如上设置，两幅图像具有相同的图像平面，图像的行是垂直对齐的，那么称图像是经过矫正的。该设置在机器人学中很常见，被称为立体平台。

立体重建就是恢复深度图，图像中每个像素的深度都需要计算出来。在计算视差图这一立体重建算法中，要对每个像素尝试不同的偏移，并按照局部图像周围归一化的互相关值选择具有最好分数的偏移，然后记录下该最佳偏移。因为每个偏移在某种程度上对应于一个平面，所以该过程称为扫平面法。我们使每个像素周围的图像块来计算归一化的互相关，然后对该像素周围局部像素块中的像素求和。这一部分使用图像滤波器来快速计算。