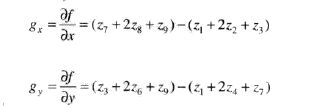《数字图像处理》-(2)灰度变换与空间滤波&halcon代码
1灰度变换
最简单的形式是邻域为1x1的尺度 (即一单个像素)。在这种情况下(仅依赖于f在(x,y)点的值,T操作成为灰度级变换函数(也叫做强度映射),形式为:
s=T®
s和r是所定义的变量,分别是f(x,y)和g(x,y)在任意点(x,y)的灰度值。
1.1图像反转
灰度级范围为丨0,L-1丨的图像反转可由示于前图的反比变换获得,表达式为:
s=L-1-r
用这种方式倒转图像的强度产生图像反转的对等图像。这种处理尤其适用于增强嵌入于图像暗色区域的白色或灰色细节,特别是当黑色面积占主导地位时:

1.2对数变换
![]()
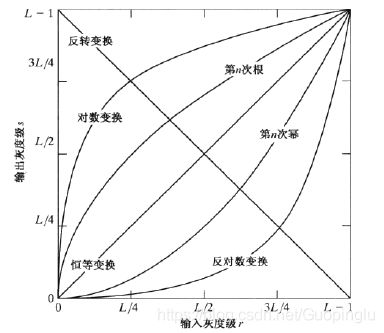
此 种 变 換 使 一 窄 带 低灰度输入图像值映射为一 宽 带 输 出 值 .相 对 的 是 输 入 灰 度 的 高 调 整 值 .可 以 利用这种变换来扩展被压 缩的高值图像中的暗像。对图像取log,差值取log之后做线性拉伸,拉伸到原来的灰度等级,使的亮区域和暗区域形成差别。由右图可知,对数变换主要作用是拉大灰度值较低的区域,压缩灰度值较高的区域,适用于灰度较暗的图像,使图像较暗的细节显示出来。适用于本身图像具有较大范围的灰度波动,最亮的更突出,如若本身灰度变化在一定范围,其作用低于其他变换。
1.3 幂次变换的基本形式:
s =cr^γ
其中,c和γ为正常数。γ>1或γ<1对图像的处理有相反的效果。当γ<1时,于对数变换有相同的效果,

幂律变换还可以用来进行对比度增强。对于整体比较暗的图像,选择一个小于1的伽马值,来扩展灰度级;对于整体比较亮的图像,选择一个大于1的伽马值,来压缩灰度值。
read_image (Image, 'printer_chip/printer_chip_01')
*1 反转图像
invert_image (Image, ImageInvert)
*2 对数变换
log_image (Image, LogImage, 'e')
*3 对数变换
pow_image (ImageConverted, PowImage,2)
*此时得到的图像格式为real
*转换第一种直接scale_image_max,
scale_image_max (LogImage, ImageScaleMax)
*第二种先放大在转换格式,直接转换格式会损失掉小数值
min_max_gray (LogImage, LogImage, 0, Min, Max, Range)
scale_image_range (LogImage, ImageScaled, Min, Max)
convert_image_type (ImageScaled, ImageConverted, 'byte')
2直方图处理
直方图均衡化可以增强图像的对比度,直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。
某一灰度等级变换到其累计直方图所在位置的灰度等级。
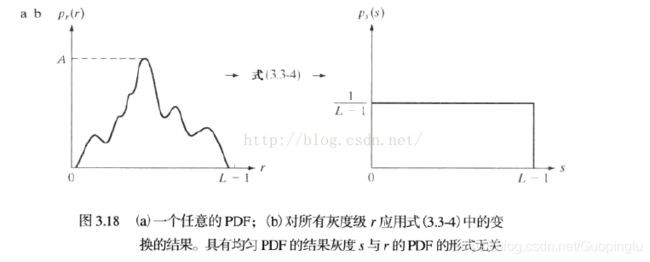
理解:也就是说所占面积比例与该灰度所占灰度范围的比例一致。例如灰度为127的前半部分面积概率,理想情况下为0.5,则将前半部分和为0.5的灰度值变换到127.。公式为直方图均衡化变换原理

直方图规定化也就是将该图像某一灰度等级变换到该灰度等级变换到指定图像的其累计直方图对应的灰度等级上。
read_image (Image, 'printer_chip/printer_chip_01')
gray_histo (Image, Image, AbsoluteHisto, RelativeHisto)
equ_histo_image (Image, ImageEquHisto)
3空间滤波基础
空间滤波的机理示于下图 .该 处 理 就 是 在 待处理图像中逐点地移动掩模 .在每一点 (x,y)处,滤波器在该 点的响应通过事先义的关系来计算 .对于线性空间滤波其响应由 滤波器系数与滤波掩模扫过区域的相应像索值的乘积之和 给出:

空间相关与卷积
相关:滤波器模板移过图像并计算每个位置的乘积之和。
卷积:卷积的机理相似,但需要先将模板旋转180°。

相关:
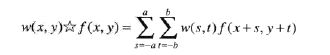
卷积:
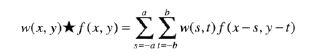
卷积的重要特性是满足乘法交换律。此处先理解卷积,后续会讲到卷积的具体用处。
3.1线性滤波
平滑线性空间滤波器的输出(响应)是包含在滤波掩模邻域内像素的简单平均值。平滑滤波器用滤波掩模确定的邻域内像素的平均灰度值去代替图像的每个像素点的值,这种处理减小了图像灰度的“尖锐”变化。

第一个均值滤波器:标准模式下的像素平均值
![]()
第二个均值滤波器:加权平均值。认为一些像素比其他的更为重要,即中心的像素的权值最大,离掩膜中心越远权值就越小。处理时就是以不同的系数乘以对应的像素的灰度值。

高斯滤波
高斯滤波也就是每个点的权重是通过高斯函数也就是正太分布函数得来的。
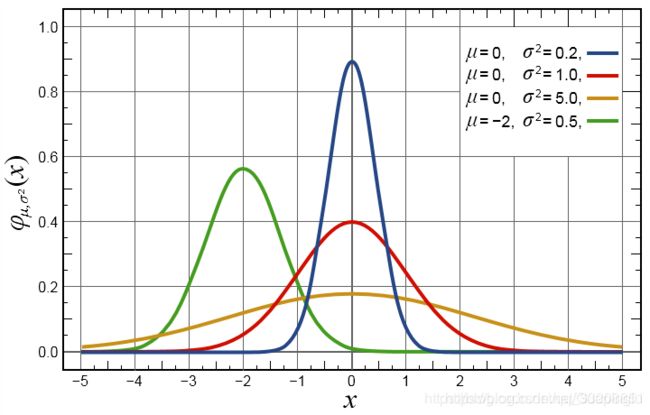

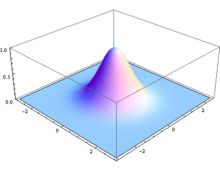
权重矩阵:
假定中心点的坐标是(0,0),那么距离它最近的8个点的坐标如下:
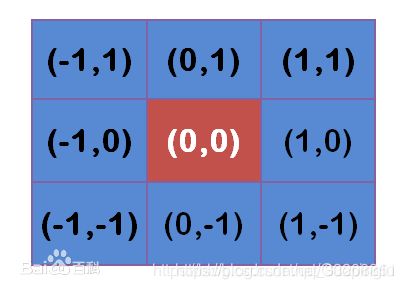
更远的点以此类推。
为了计算权重矩阵,需要设定σ的值。假定σ=1.5(σ值越大图像越平滑/模糊),则模糊半径为1的权重矩阵如下:

这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵

3.2统计排序(非线性)滤波器
中值滤波器中值滤波器是一种非线性的空间滤波器,它的响应基于图像滤波器包围的图像区域中像素的排序,然后由统计结果决定的值代替中心像素的值。
中值滤波器是将像素(在中值计算中包括的原像素值)邻域内灰度的中值代替该像素的值。一个数值集合的中值e是这样的数值,即,数值集合中,有一半小于或等于e,还有一半大于或等于s 。为 了 对 一 幅图像上的某个点做中值滤波处理,必须先将掩模内欲求的像素及其邻域的像素值排序,确定出中值,并将中值賦予该象素点.
中值滤波器的使用非常普遍,这是因为对于一定类型的随机噪声,它提供了一种优秀的去噪能力,比小尺寸的线性平滑滤波器的模糊程度明显。

中值滤波器:在邻域内排序后取中位数的值
最大值最小值滤波器:在邻域内排序后取最大值最小值
中点滤波器:哎邻域内取最大值和最小值的平均值
阿尔法滤波器:去掉最大的d/2个点,去掉最小的d/2个点(总共d个点,mn-d是剩下的个数)然后对剩下的点求平均值。特殊情况:当d=0时(去掉d/2=0/2=0个最大及最小的点),为算术平均滤波器;当d=mn-1时(去掉d/2=(mn-1)/2个最大及最小的点,剩下中间的一个,因为掩膜时奇数x奇数,所以中位数不可能剩两个),为中值滤波器。
中值滤波器对处理椒盐噪声(脉冲噪声)比较明显。噪声以黑白点的形式叠加在图像上。
read_image (Image, 'printer_chip/printer_chip_01')
mean_image (Image, ImageMean, 9, 9)
gauss_filter (Image, ImageGauss, 5)
median_image (Image, ImageMedian, 'circle', 5, 'mirrored')
3.3自适应滤波器
自适应滤波是近年以来发展起来的一种最佳滤波方法
自适应滤波器的特点:
1.没有关于待提取信息的先验统计知识
2.直接利用观测数据依据某种判据在观测过程中不断递归更新
3.最优化
自适应滤波器可以分为线性自适应滤波器和非线性自适应滤波器。非线性自适应滤波器包括Voetlrra滤波器和基于神经网络的自适应滤波器。非线性自适应滤波器具有更强的信号处理能力。但是,由于非线性自适应滤波器的计算较复杂,实际用得最多的仍然是线性自适应滤波器。
自适应滤波器是能够根据输入信号自动调整性能进行数字信号处理的数字滤波器。作为对比,非自适应滤波器有静态的滤波器系数,这些静态系数一起组成传递函数。
4锐化
锐化处理的主要目的是突出灰度的过度部分。锐化是通过增强高频分量来减少图像中的模糊,增强图像细节边缘和轮廓,增强灰度反差,便于后期对目标的识别和处理。锐化处理在增强图像边缘的同时也增加了图像的噪声。方法通常有微分法和高通滤波法。



数字图像中的边缘在灰度上常常类似于斜坡过度,边缘存在过渡带,这样就导致图像的一阶微分产生较粗的边缘。因为沿着斜坡的微分非零。另一方面,二阶微分产生由零分开的一个像素宽的双边缘。因此二阶微分在增强细节方面要比一阶微分好得多,这是一个适合锐化图像的理想特性。
4.1拉普拉斯算子
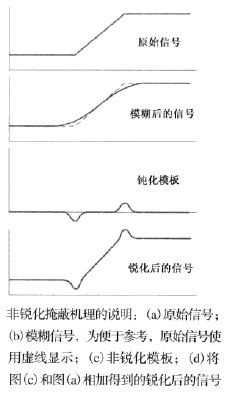
4.2非锐化遮蔽
4.3 sobel算子:
read_image (Image, 'printer_chip/printer_chip_01')
*拉普拉斯
laplace (Image, ImageLaplace, 'absolute', 3, 'n_4')
add_image (ImageLaplace, Image, ImageResult, 1, 0)
*sobel 算子
sobel_amp (ImageResult, EdgeAmplitude, 'sum_abs', 3)
add_image (EdgeAmplitude, Image, ImageResult1, 1, 0)
*非锐化遮蔽
mean_image (Image, ImageMean, 9, 9)
sub_image (Image,ImageMean, ImageSub, 1,0)
add_image (ImageSub, Image, ImageResult2, 1, 0)
5一些边缘检测的经验
突变型细节:通过一阶微分的极大值点,二阶微分的零点可以检测出来;
细线型细节,通过一阶微分的零点,二阶微分的极小值点可以检测出来;
渐变型细节,一般情况下突变幅度小、定位难,不易检测,但二阶微分的信息比一阶微分多,需进行综合考虑.
6参考:
https://blog.csdn.net/baishuiniyaonulia/article/details/98480583
https://blog.csdn.net/qq_33208851/article/details/95349944
https://blog.csdn.net/qq_33208851/article/details/96626513
<数字图像处理>