动态规划之区间DP专题
动态规划之区间DP专题
什么是区间DP
所谓区间dp,就是在一个区间上进行的dp, 一般通过将大区间分割成小区间进行dp。
区间型动态规划,又称为合并类动态规划,是线性动态规划的扩展,它在分阶段地划分问题时,与阶段中元素出现的顺序和由前一阶段的区间中哪些元素合并而来有很大的关系。
区间动归状态转移方程及一般动规过程:
for k:=1 to n-1 do //区间长度
for i:=1 to n-k do //区间起点
for j:=i to i+k-1 do //区间中任意点
dp[i,i+k]:=max{dp[i,j] + dp[j+1,i+k] + a[i,j] + a[j+1,i+k]};1. 状态转移方程字面意义:寻找区间dp[i,i+k]的一种合并方式dp[i,j] + dp[j+1,i+k],使得其值最大或最小。
2. 区间长度k必须要放到第一层循环,来保证方程中状态dp[i,j]、dp[j+1,i+k]值在dp[i,i+k]之前就已计算出来。
3. 其中a[i,j]+a[j+1,i+k]可以不要,也可以灵活多变,指的是合并区间时产生的附加值。
【NOI1995】石子合并
【在线测试提交传送门】
【问题描述】
在一个圆形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 设计出1个算法,计算出将N堆石子合并成1堆的最小得分和最大得分。
【输入格式】
数据的第1行试正整数N,1≤N≤100,表示有N堆石子.第2行有N个数,分别表示每堆石子的个数。
【输出格式】
输出共2行,第1行为最小得分,第2行为最大得分。
【输入样例1】
4 4 5 9 4
【输出样例1】
43 54
【解题思路】
看到题目,很像贪心,采用尽可能逼近目标的贪心法来逐次合并。如样例数据,从最上面一堆开始,沿顺时针方向排成一个环,要计算得分最小时,第一次去相邻得分最小的4,4两堆合并,得分为8分,合并后剩下3堆,分别为8 5 9;再选择相邻得分最小的5,8合并,得13分,最后选9和13合并,得22分,总共分数为43,与样例输出一样,好像这种贪心是正确的。
其实不然,这种策略存在反例。如6堆石子,从最上面一堆顺时针数起,石子数分别为3,4,6,5,4,2,采用贪心策略合并时,合并过程如下:

但是经过反复推敲,可以得到一种总得分更小的合并方案,合并过程如图2。
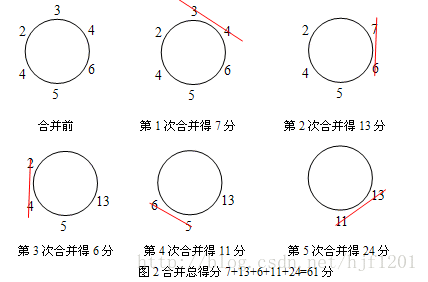
显然,图2的合并方案更优。样例数据其实是一种用贪心策略可以解决问题的假象,导致很多选手使用了贪心策略,从而丢了很多分。下面来分析第二种合并方案。从后往前推,有图2可以看出,6堆石子合并的最小得分方案min{merge(1,2,3,4,5,6)}是由merge(1,2,3)和merge(4,5,6)得来的,上述中,merge表示合并, 1,2,3,…表示第1,2,3,…堆的石子。merge(1,2,3)时,它有两种合并方案,即先merge(1,2)两堆,再将1,2合并得结果与第3堆合并,merge(merge(1,2),3);或者先merge(2,3),然后merge(1,merge(2,3))。
第一种合并方案(3+4)+6的合并得分为7+13=20;
第二种合并方案3+(4+6)的合并得分为10+13=23。
明显第一种方案得分少。merge(4,5,6)时,也同样有两种方案。合并1到6堆得过程如下:
合并1堆:1,2,…,6;
合并2堆:12,23,…,61;
合并3堆:123,234,…,612;
合并4堆:1234,2345,…,6123;
合并5堆:12345,23456,…,61234;
合并6堆:123456,234561,…,612345。
因此,从第i堆开始合并到第j堆时,它的值可以为第i堆+min{merge(i+1,i+2,…,i+j-1)}。如从第1堆开始合并4堆时,它可以为第1堆+min{merge(2,3,4)},也可以为min{merge(1,2)+merge(3,4)},也可以为min{merge(1,2,3)}+第4堆,共3种来源,与区间的合并有关。依次类推,合并到6堆时,去从第i堆开始合并6堆得最小值,即得到合并得总的最小值。所以,此问题具备最优子结构的性质,而且无后效性。
阶段:合并得堆数。
状态:dp[i,j]。表示从第i堆起,顺时针合并j堆得总得分最小值,它包括合并前j-1堆的最小总得分加上这次合并得得分,用sum[i,j]表示这次合并得得分。合并时的堆数可以表示为序列{第i堆,第i+1堆,….,第(i+j-2) mod n+1堆}。序列总得来的方案有很多种,我们用子序列1和子序列2表示,如子序列1为{第i堆},子序列2为{第i+1堆,…,第(i+j-2)mod n+1堆}。子序列1和子序列2相邻,所以,假如子序列1为k堆,则子序列2为j-k堆。由此,可以得到动规方程:
dp[i,j]=min{dp[i,k]+dp[i+k,j-k]+sum[i,j] , 1≤k≤j-1}
stone[i]表示初始时每堆的石子数,则动规的初始条件为:dp[i,1]=0
动规的边界为1≤i<n,1≤j≤n。求最大得分与最小得分方法一样,只是在计算时反一下就可以了。
从石子合并得算法来看,状态dp[i,j]与合并时的起始位置和前j-1个合并区间有关,是典型的区间型动态规划。
#include//序列一序列二合并也会得分而且得的分都是sum[i][j]因为加法满足结合律。
fmax[i][j]=sum[i][j]+fmax[next][j-k]+fmax[i][k];
if(fmin[i][j]>sum[i][j]+fmin[next][j-k]+fmin[i][k])
fmin[i][j]=sum[i][j]+fmin[next][j-k]+fmin[i][k];
}
}
}
//哪个位置当第一次合并
int min=maxn ,max=0;
for(i=1;i<=n;++i)
{
if(min>fmin[i][n])
min=fmin[i][n];
if(maxprintf("%d\n%d",min,max);
return 0;
}
【NOIP2000提高】乘积最大
【在线测试提交传送门】
【问题描述】
今年是国际数学联盟确定的“2000――世界数学年”,又恰逢我国著名数学家华罗庚先生诞辰90周年。在华罗庚先生的家乡江苏金坛,组织了一场别开生面的数学智力竞赛的活动,你的一个好朋友XZ也有幸得以参加。活动中,主持人给所有参加活动的选手出了这样一道题目: 设有一个长度为N的数字串,要求选手使用K个乘号将它分成K+1个部分,找出一种分法,使得这K+1个部分的乘积能够为最大。 同时,为了帮助选手能够正确理解题意,主持人还举了如下的一个例子: 有一个数字串:312, 当N=3,K=1时会有以下两种分法:(1) 3*12=36 (2)31*2=62 这时,符合题目要求的结果是:31*2=62 现在,请你帮助你的好朋友XZ设计一个程序,求得正确的答案。
【输入格式】
程序的输入共有两行: 第一行共有2个自然数N,K(6≤N≤40,1≤K≤6) 第二行是一个长度为N的数字串
【输出格式】
输出共1行,1个整数,表示所求得的最大乘积。
【输入样例1】
4 2 1231
【输出样例1】
62
【解题思路】
从题意来看,“*”号的插入方式非常重要。比如样例,如果插入位置为1*23*1时,结果为23;插入位置为12*3*1时,结果为36;插入位置为1*2*31时,结果为62,这种方式的值最大。从这点来看,本题与石子合并非常相像。设输入的数字串味s,在s1,...,si(2≤i≤n)中插入j个“*”时,假设在s1,..,sk中插入了j-1个“*”号,则乘式中第j个“*”号后边的式子sk+1,..,si为常量;设f[i,j]表示在长度为i的数字串中插入j个“*”的最大乘积,要得到f[i,j]的最大值时,就要得到max{f[k,j-1]*sk+1...sn (j≤k≤i-1)}的值;一一枚举k的位置,即可得到max{f[k,j-1]*sk+1..sn}的值。最后输出f[n,m]的值即可。显然,这一问题具备最优子结构的性质,且无后效性,也是区间型动规类问题。
阶段:数字串的长度;
状态:长度为i的数字串中插入的“*”的个数;
决策:第j个“*”的最佳插入位置。
#includereturn y;
if(lx>ly) return x;
for(int i=lx;i>=1;--i)
{
if(x.ans[i]>y.ans[i]) return x;
if(x.ans[i]return y;
}
return x;
}
int main()
{
scanf("%d%d",&n,&K);
cin>>s;
for(int i=1;i<=n;++i) a[i]=s[i-1]-'0';
for(int i=1;i<=n;++i)
for(int j=i;j>=1;--j)
dp[0][i].ans[++dp[0][i].len]=a[j];
for(int i=2;i<=n;++i)
for(int k=1;k<=min(K,i-1);++k)
for(int j=k;j1][j],j+1,i));
for(int i=dp[K][n].len;i>=1;--i)
printf("%d",dp[K][n].ans[i]);
return 0;
}
【NOIP2006提高组】能量项链
【在线测试提交传送门】
【问题描述】
在Mars星球上,每个Mars人都随身佩带着一串能量项链。在项链上有N颗能量珠。能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样,通过吸盘(吸盘是Mars人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为r,尾标记为n,则聚合后释放的能量为m*r*n(Mars单位),新产生的珠子的头标记为m,尾标记为n。
需要时,Mars人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设N=4,4颗珠子的头标记与尾标记依次为(2,3) (3,5) (5,10) (10,2)。我们用记号⊕表示两颗珠子的聚合操作,(j⊕k)表示第j,k两颗珠子聚合后所释放的能量。则第4、1两颗珠子聚合后释放的能量为:(4⊕1)=10*2*3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为((4⊕1)⊕2)⊕3)=10*2*3+10*3*5+10*5*10=710。
【输入格式】
输入文件的第一行是一个正整数N(4≤N≤100),表示项链上珠子的个数。 第二行是N个用空格隔开的正整数,所有的数均不超过1000。第i个数为第i颗珠子的头标记(1≤i≤N),当1≤i<N时,第i颗珠子的尾标记应该等于第i+1颗珠子的头标记。第N颗珠子的尾标记应该等于第1颗珠子的头标记。 至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
【输出格式】
输出只有一行,是一个正整数E(E≤2.1*10^9),为一个最优聚合顺序所释放的总能量。
【输入样例1】
4 2 3 5 10
【输出样例1】
710
【解题思路】
用head表示第i颗珠子的头标记,用tail表示尾标记,合并两颗相邻珠子所释放的能量为:energy=head[i]*tail[i]*tail[i+1]
合并时不一定按输入顺序合并,与石子合并问题类似,第n次合并,可以归结到第n-1次合并,具有明显地动规性质。用f[I,j]表示从第i颗珠子合并到第j颗珠子时产生的最大能量,用k表示最后一次的合并位置,则有: dp[i,j]=max{dp[i,k]+dp[k+1,j]+head[i]*tail[k]*tail[j] , i≤k≤j} 上式中,dp[i,k]表示第i颗到第k颗珠子产生的最大能量,dp[k+1,j]表示合并第k+1颗到第j颗时产生的最大能量,head[i]*tail[k]*tail[j]表示最后一次合并时产生的能量。dp[i,j]的值,分成两个区间,取最大值,是典型的区间型动规。最后一次合并时,产生的能量为什么是head[i]*tail[k]*tail[j]呢?假设有5颗珠子,每颗珠子的能量为10,2,3,5,6,当i=1,j=4,k=2时,如图:
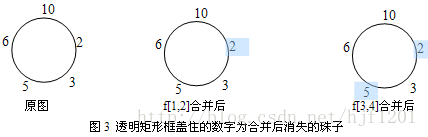
由图可以看出,合并dp[1,2],dp[3,4]后,还剩下1,3,5三颗珠子(从最上面开始顺时针数),此时1号珠子head[1]=10,tail[1]=3,相当于原图的tail[2];3号珠子tail[3]=6,相当于原图的tail[4]。最后合并dp[1,4]时,相当于合并1,3两颗珠子,产生的能量为最右边图的10*3*6,相当于原图中的head[1]*tail[2]*tail[4],即为上式中的head[i]*tail[k]*tail[j]。
由于项链是一个环,我们把项链以2*n-1长度,一水平线的形式平铺在桌面上,从左到右逐一扫描,得出最大值。
实现:
重点就是将整体划分为区间,小区间之间合并获得大区间
状态转移方程的推导如下
一、将珠子划分为两个珠子一个区间时,这个区间的能量=左边珠子*右边珠子*右边珠子的下一个珠子
二、区间包含3个珠子,可以是左边单个珠子的区间+右边两珠子的区间,或者左边两珠子的区间右边+单个珠子的区间
即,先合并两个珠子的区间,释放能量,加上单个珠子区间的能量(单个珠子没有能量。。)
Energy=max(两个珠子的区间的能量+单个珠子区间的能量,单个珠子的区间的能量+两个珠子的区间的能量 )
三、继续推4个珠子的区间,5个珠子的区间。
于是可以得到方程:Energy=max(不操作的能量,左区间合并后的能量+右区间合并后的能量+两区间合并产生能量)
两区间合并后产生的能量=左区间第一个珠子右区间第一个珠子总区间后面的一个珠子
#include=1;j--){//从i开始向前推
for(int k=j;k//k是项链的左右区间的划分点
s[j][i]=max(s[j][i],s[j][k]+s[k+1][i]+e[j]*e[k+1]*e[i+1]);
//状态转移方程:max(原来能量,左区间能量+右区间能量+合并后生成能量)
if(s[j][i]>maxn)maxn=s[j][i];//求最大值
}
}
cout<return 0;
}
【洛谷1622】释放囚犯
【在线测试提交传送门】
【问题描述】
Caima王国中有一个奇怪的监狱,这个监狱一共有P个牢房,这些牢房一字排开,第i个紧挨着第i+1个(最后一个除外)。现在正好牢房是满的。 上级下发了一个释放名单,要求每天释放名单上的一个人。这可把看守们吓得不轻,因为看守们知道,现在牢房中的P个人,可以相互之间传话。如果某个人离开了,那么原来和这个人能说上话的人,都会很气愤,导致他们那天会一直大吼大叫,搞得看守很头疼。如果给这些要发火的人吃上肉,他们就会安静点。
【输入格式】
第一行两个数P和Q,Q表示释放名单上的人数; 第二行Q个数,表示要释放哪些人。
【输出格式】
仅一行,表示最少要给多少人次送肉吃。
【输入样例1】
20 3 3 6 14
【输出样例1】
35
【样例说明】
先释放14号监狱中的罪犯,要给1到13号监狱和15到20号监狱中的19人送肉吃;再释放6号监狱中的罪犯,要给1到5号监狱和7到13号监狱中的12人送肉吃;最后释放3号监狱中的罪犯,要给1到2号监狱和4到5号监狱中的4人送肉吃。
【数据范围】
对于50%的数据 1≤P≤100;1≤Q≤5 对于100%的数据1≤P≤1000; 1≤Q≤100;Q≤P;
【解题思路】
把要释放的人视作断点,将p个人分成q+1个区间,求合并区间至一个区间所需最小值,即可视为合并石子。 注意分成q+1个区间时的一些细节。
#include
using namespace std;
int s[110][110]={0},p,q,a[110]={0},sum[110]={0};
inline void init()
{
scanf("%d%d",&p,&q);
for(int i=1;i<=q;i++)scanf("%d",&a[i]);
a[0]=0;a[++q]=p+1;
sort(a,a+q+1);
return;
}
int main()
{
init();
for(int i=1;i<=q;i++)
sum[i]=a[i]-a[i-1]-1+sum[i-1];//前缀和,将问题转换为求几堆石子合并的最小值
for(int k=2;k<=q;k++)
for(int i=1;i<=q-k+1;i++)
{
int j=i+k-1;
for(int p=i;pif(!s[i][j]||s[i][j]>s[i][p]+s[p+1][j]+sum[j]-sum[i-1]+j-i-1)//注意j-i+1,是指合并时几个还未释放的人所需的代价
s[i][j]=s[i][p]+s[p+1][j]+sum[j]-sum[i-1]+j-i-1;
}
printf("%d",s[1][q]);
return 0;
}
【洛谷2858】奶牛零食
【在线测试提交传送门】
【问题描述】
约翰经常给产奶量高的奶牛发特殊津贴,于是很快奶牛们拥有了大笔不知该怎么花的钱.为此,约翰购置了N(1≤N≤2000)份美味的零食来卖给奶牛们.每天约翰售出一份零食.当然约翰希望这些零食全部售出后能得到最大的收益.这些零食有以下这些有趣的特性:
1.零食按照1..N编号,它们被排成一列放在一个很长的盒子里.盒子的两端都有开口,约翰每天可以从盒子的任一端取出最外面的一个;
2.与美酒与好吃的奶酪相似,这些零食储存得越久就越好吃.当然,这样约翰就可以把它们卖出更高的价钱;
3.每份零食的初始价值不一定相同.约翰进货时,第i份零食的初始价值为Vi(1≤Vi≤1000);
4.第i份零食如果在被买进后的第a天出售,则它的售价是vi×a。Vi指的是从盒子顶端往下的第i份零食的初始价值。
约翰告诉了你所有零食的初始价值,并希望你能帮他计算一下,在这些零食全被卖出后,他最多能得到多少钱。
【输入格式】
第一行,一个整数n; 接下来n行,每行一个整数表示Vi。
【输出格式】
一行,一个整数,表示最多的钱。
【输入样例1】
5 1 3 1 5 2
【输出样例1】
43
【解题思路】
dp[i][j]=max(dp[i+1][j]+a[i]*(n-l+1),dp[i][j-1]+a[j]*(n-l+1));//有两种情况一种是选开头点的那一个最优,一种是选结束点的那一个最优
#include1][n]<//最后直接输出从开头到末尾的最大值
return 0;
}
//记忆化搜索写法:
#include【POJ1141】Brackets Sequence 括号匹配
【在线测试提交传送门】
【问题描述】
定义正确的括号序列为: 1.空序列是一个正确的括号序列; 2.如果S是一个正确的括号序列,那么(S)和[S]也是正确的括号序列; 3.如果A和B是正确的括号序列,那么AB也是正确的括号序列。 例如,正确的括号序列有:(), [], (()), ([]), ()[], ()[()] 例如,不正确的括号序列:(, [, ), )(, ([)], ([(] 现在给定一个括号序列,需要你添加最少的括号,是的该括号序列是一个正确的括号序列。
【输入格式】
一行,一个括号序列,不超过100个符号。
【输出格式】
一行,一个正确的括号序列。
【输入样例1】
([(]
【输出样例1】
()[()]
【解题思路】
d[i][j]表示从i到j的范围内最少需要添加的括号数 pos[i][j]表示i到j的范围内从pos[i][j]处分开进行添加可使得括号数最小,为-1表示无需分开添加 若s[i]和s[j]组合为"()"或"[]",则说明已经配对,只需处理i和j内部的序列,且暂时令pos[i][j]=-1; 然后枚举i到j中的分界点,查看是否存在k使得d[i][j]>d[i][k]+d[k][j](状态转移方程),若存在, 则说明将i和j从k处分离成两部分进行处理可使得添加的括号数更小,此时令pos[i][j]=k,记录下此分界点 show函数说明:利用递归输出匹配后的括号序列 1、如果i>j,越界,则返回 2、如果i==j,说明只处理的一个括号,输出对应的配对括号对即可 3、如果i<j,首先判断pos[i][j]?-1,若相等,说明i和j之间无需分解, 先输出左边,然后递归输出中间,最后输出右边括号;若不相等,则递归 输出i到pos[i][j],pos[i][j]+1到j两部分
#include1;
for(k=1;k//表示i和j之间的间隔
for(i=0;ichar right=s[i+k];
char left=s[i];
d[i][i+k]=INF; //此条语句不能少,假如下面的if不执行,则for中判断就会出错d[i][i+k]未赋值
if(left=='('&&right==')'||left=='['&&right==']')
{
d[i][i+k]=d[i+1][i+k-1];
pos[i][i+k]=-1;
}
for(j=i;j//靠左分界
if(d[i][i+k]>d[i][j]+d[j+1][i+k])
{
pos[i][i+k]=j;
d[i][i+k]=d[i][j]+d[j+1][i+k];
}
}
}
void show(int i,int j)
{
if(i>j) return;
if(i==j)
{
if(s[i]=='('||s[i]==')') cout<<"()";
else cout<<"[]";
}
else
{
if(pos[i][j]==-1)
{
cout<1,j-1);
cout<else
{
show(i,pos[i][j]);
show(pos[i][j]+1,j);
}
}
}
int main()
{
cin>>s;
int len=strlen(s);
Match(len);
show(0,len-1);
cout<return 0;
}
【HDU4745】Two Rabbits
【在线测试提交传送门】
【问题描述】
有两只兔子Tom和Jerry,他们在玩一个游戏。n块石头围成一圈,编号依次为1到n,第1块石头和第2块石头、第n块石头相邻。第i块石头的重量是ai。 兔子可以从一块石头跳到另外一块石头上,Tom顺时针跳,Jerry逆时间跳。 开始时,他们可以选择一块石头,站在上面,每一轮,Tom选择跳到一块他自己没有跳上去过的石头,Jerry也是一样,只是方向不同。 在每一个时间,两只兔子所站的石头的重量必须相同。而且跳的时候,不能越过已经跳过的石头。例如,如果Tom已经跳到过第2块石头,他就不能从第1块石头跳到第3块石头,或者从第n块石头跳到第4块石头。 游戏过程中,Tom和Jerry可以同时站在同一块石头上。 请计算,他们最多可以进行多少轮游戏。
【输入格式】
输入最多包含20组测试数据,对于每组测试数据: 第一行,一个整数n,表示石头的数量; 第二行,n个整数,依次表示每一块石头的重量ai; 当n=0时,表示输入结束。
【输出格式】
对于每组测试数据输出一行一个整数,表示最多的游戏轮数。
【输入样例1】
1 1 4 1 1 2 1 6 2 1 1 2 1 3 0
【输出样例1】
1 4 5
【样例解释】
对于第2个样例,Tom的序列是1,2,3,4;Jerry的序列是1,4,3,2; 对于第3个样例,Tom的序列是1,2,3,4,5;Jerry的序列是4,3,2,1,5。
【数据范围】
1 ≤ n ≤ 1000, 1 ≤ ai ≤ 1000
【解题思路】
区间DP, 转换成求最长非连续的回文串 将数组扩大为2倍,计算每个区间的最长非连续的回文串 状态转移方程dp[i][j] = max(dp[i][j], dp[i+1][j], dp[i][j-1], a[i]==a[j]?a[i+1][j-1]+2:0) 注意像字符串1221,计算出来的dp[0][3] = 4,而不是2 所以最后结果肯定是只有n个字符,或者n-1的字符加个1
#include scanf("%d", &a[i]);
a[n+i] = a[i];
}
//1个字符时,肯定是1了
for(int i=0; i<2*n; i++)
dp[i][i] = 1;
for(int len=2; len<=2*n; len++)
for(int i=0; i+len<2*n; i++)
{
int j = i+len-1;
if(a[i]==a[j])
{
dp[i][j] = max(dp[i][j], dp[i+1][j-1]+2);
}
dp[i][j] = max(dp[i][j], max(dp[i+1][j], dp[i][j-1]));
}
int ans = 0;
//n个字符
for(int i=0; i1]);
//n-1个字符,最后一个当做公共的起点,所以+1
for(int i=0; i2]+1);
printf("%d\n", ans);
}
return 0;
}