【树的点分治】【ST表】BZOJ 3784 —— 树上的路径

题目传送门(权限题警告)

总有一个序列，能够满足题目中所需求的一切性质。—— 鲁迅 （没说过）

这里引入一个叫做点分治序列的东西,它通过下列步骤生成.
1.找到当前树的重心,将重心加入序列.
2.从重心出发,dfs遍历整个树,将遍历到的点加入序列.
3.将与重心相连的边断掉,生成若干子树,对于每一个子树重复上述过程.

显然,点分治序列不是唯一的.
例如下图的一个点分治序列是$47109625831710910962583185531$

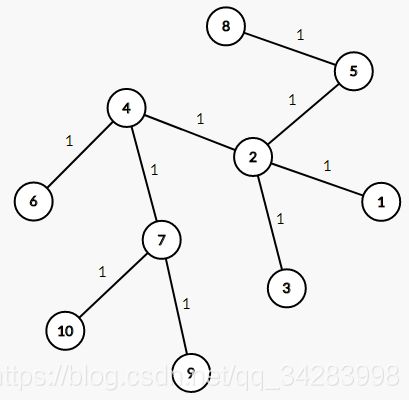
对于一个已经确定的重心,我们暂时只考虑经过这个重心的路径,即从它的某一个子树中的点,到另一个子树中的某个点(也可以是这个重心).这样这条路径就被分为两段,不妨分开处理,只考虑重心到某个点的距离,对于路径而言则只需要将路径的两个端点到重心的距离相加.

因此,我们考虑确定路径的一个点,对于另一个点的选取显然是有范围限制的.即在这个点所在子树前,遍历的所有点以及目前的重心,都可以作为路径的另一个端点.

此时点分治序列的性质就体现出来了.
可以发现,能成为另一个端点的点,在点分治序列上是连续的.可以预处理出来(l,r).然后只需用ST表,即可快速询问哪一个点作为另一个端点会使得当前路径最大.塞入一个优先队列中输出答案.

接着还有一个问题,当优先队列队首所表示的路径出队后,实际上对于这个点,经过相应重心的第二长路径,第三长路径等是并没有加入队列的.
此时可以看作将点分治序列上(l,r)从最大值值处断开,分为两个区间继续处理即可将剩下的情况处理出.这也是为什么需要优先队列的原因.

#include
#include
#include
using namespace std;

typedef pair<int,int> pii;
const int MAXN=50005;
const int MAXM=8e5;
const int INF=0x3f3f3f3f;
#define mp(A,B,C,D) make_pair(make_pair(A,B),make_pair(C,D))


int n,m,ecnt,root,maxv=INF,ncnt,tot;
int head[MAXN],dep[MAXM],l[MAXM],r[MAXM];
int ST[MAXM][20],siz[MAXN],vis[MAXN],log[MAXM];
struct edge{int v,val,nxt;}E[MAXN*2];
priority_queue<pair<pii,pii> > q;

void addedge(int u,int v,int val){
    E[++ecnt]=(edge){v,val,head[u]};
    head[u]=ecnt;
}

void pre(int u,int fa=0){
    int maxson=0; siz[u]=1;
    for(int i=head[u];i;i=E[i].nxt){
        int v=E[i].v;
        if(v==fa||vis[v]) continue;
        pre(v,u);
        siz[u]+=siz[v];
        maxson=max(maxson,siz[v]);
    }
    if(max(maxson,tot-siz[u])<maxv)
        root=u,maxv=max(maxson,tot-siz[u]);
}

void work(int u,int fa,int dep){
    ::dep[++ncnt]=dep,l[ncnt]=l[ncnt-1],r[ncnt]=r[ncnt]?r[ncnt]:r[ncnt-1];
    for(int i=head[u];i;i=E[i].nxt){
        int v=E[i].v,val=E[i].val;
        if(v==fa||vis[v]) continue;
        work(v,u,dep+val);
    }
}

void dfs(int u,int fa=0){
    vis[u]=1;
    ::dep[++ncnt]=0,l[ncnt]=ncnt,r[ncnt]=ncnt-1;
    for(int i=head[u];i;i=E[i].nxt){
        int v=E[i].v,val=E[i].val;
        if(v==fa||vis[v]) continue;
        r[ncnt+1]=ncnt;
        work(v,u,val);
    }
    for(int i=head[u];i;i=E[i].nxt){
        int v=E[i].v;
        if(v==fa||vis[v]) continue;
        tot=siz[v],maxv=INF;
        pre(v,u);
        dfs(root);
    }
}

inline int ms(int x,int y){return dep[x]>dep[y]?x:y;}

int query(int a,int b){
    if(a>b) return 0;
    int k=log[b-a+1];
    return ms(ST[a][k],ST[b-(1<<k)+1][k]);
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;i++){
        int u,v,val;
        scanf("%d%d%d",&u,&v,&val);
        addedge(u,v,val);
        addedge(v,u,val);
    }
    tot=n,maxv=INF;
    pre(1);
    dfs(root);
    for(int i=1;i<=ncnt;i++) ST[i][0]=i;
    for(int i=2;i<=ncnt;i++) log[i]=log[i>>1]+1;
    for(int j=1;(1<<j)<ncnt;j++)
        for(int i=1;i+(1<<j)-1<=ncnt;i++)
            ST[i][j]=ms(ST[i][j-1],ST[i+(1<<j-1)][j-1]);
    for(int i=1;i<=ncnt;i++){
        if(l[i]>r[i]) continue;
        q.push(mp(dep[i]+dep[query(l[i],r[i])],i,l[i],r[i]));
    }
    for(int i=1,x,y,a,b,c,d;i<=m;i++){
        pii t1=q.top().first,t2=q.top().second;
        q.pop();
        printf("%d\n",t1.first),x=t1.second,a=t2.first,b=t2.second,y=query(a,b);
        c=query(a,y-1),d=query(y+1,b);
        if(c) q.push(mp(dep[x]+dep[c],x,a,y-1));
        if(d) q.push(mp(dep[x]+dep[d],x,y+1,b));
    }
}