启发式寻路算法--曼哈顿距离
曼哈顿距离
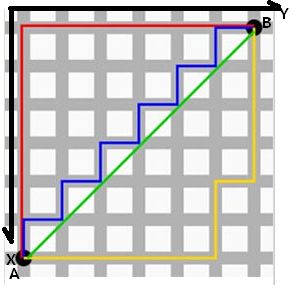
曼哈顿距离又称马氏距离、出租车距离。如下图所示:
注:<1>白色表示障碍物 <2> 灰色表示可走路径
从图可知,A点到B点中,红线代表曼哈顿距离,绿色代表欧氏距离,也就是我们说的直线距离,而蓝色和黄色代表等价的曼哈顿距离。为什么说黄色和蓝色等价于曼哈顿距离呢?我们将图再进行处理:
处理图片后,定义出X轴和Y轴,可以一目了然,分析蓝色线和黄色线。
1:蓝色线走的横向距离就是Y1+Y2+....+Yn,竖向距离就是X1+X2+...+Xn
2:黄色线走的横向距离就是两段即Y1+Y2,竖向距离也是两段X1+X2
综上两点,蓝色线走的x轴距离、y轴距离等于黄色线的x轴和y轴距离。所以,黄色线和蓝色线在x轴和y轴距离就是红色线的距离,即等价于曼哈顿距离。
启发式寻路算法
启发式寻路算法就是根据曼哈顿距离而来,我们可以利用其进行马哈顿距离估值。
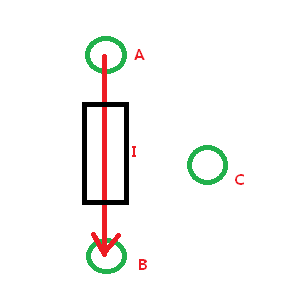
1>假设从A点到B点,中间有障碍物I
2>在寻路中,我们肯定要绕过障碍物I到达B点,所以,我们要寻找下一点c为过度,到达B点。所以,引出两个关键说明,即是实际代价(g)和预估代价(h)。
如图,实际代价(g),就是A点到达C点实际需要的距离。
3>当过渡到c点后,我们还需要在c点处对目标点B点的距离进行估值,也就是下图的预估代价(h),因为这里仅仅是举出一个过渡点C,现实开发中,可不止一个过渡点c喔,有可能有D,E,F....点等。所以,每走到一个新的点上,我们需要再一次预估此点到目标终点的距离。
4>这就是启发式寻路算法,包含实际代价(g)和预估代价(h),所以我们不难得出表达式f(n)=g(n)+h(n)。
启发式寻路算法在实际开发中非常常用,比如地图算最短距离,游戏地图等等。