西瓜书学习笔记——第十二章：计算学习理论

12.1 基础知识

计算机学习理论研究的是关于通过计算来进行学习的理论，即关于机器学习的理论基础，其目的是分析学习任务的困难本质，为学习算法提供理论保证。例如：在什么条件下可进行有效的学习，需要多少训练样本才能获得较好的精度等。

泛化误差与经验误差

• 经验误差：学习器在某个特定的数据集D上的预测误差
• 泛化误差：学习器在总体上的预测误差

而在实际问题中，我们往往不能得到总体且数据集D是通过独立同分布采样得到的，因此我们常常使用经验误差作为泛化误差的近似。

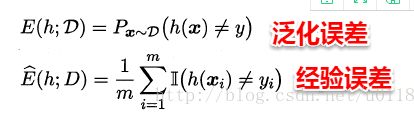
12.2 PAC学习

对于机器学习算法，学习器是为了寻找合适的映射规则，即如何从条件属性得到目标属性。从样本空间到标记空间存在着很多的映射，称之为概念$c$，它决定着示例$x$的真实标记$y$

• 若对任何示例$(x,y)$都有$c(x)=y$成立，则称$c$为目标概念，所有希望学得的目标概念$c$组成的集合为“概念类”
• 给定学习算法，它所考虑的所有可能概念的集合称为“假设空间”，其中单个的概念称为“假设”
• 若一个算法的假设空间包含目标概念，则称该数据集对算法是“可分的”，也称“一致的”
• 若一个算法的假设空间不包含目标概念，则称该数据集对算法是“不可分的”，也称“不一致的”

给定一个数据集D，我们希望模型学得的假设h尽可能与目标概念一致，即以较大的概率学得误差满足预设上限的模型，这就是概率近似正确的含义。

这样的学习算法能以较大的概率(至少1-$\delta$)学得目标概念$c$的近似(误差最多为$ϵ$)，即该算法的输出假设已经十分接近目标概念。

若将样本数量考虑进来，有：

若将运行时间考虑进来，有：


显然，PAC学习中的一个关键因素是假设空间复杂度，对于某个学习算法，若假设空间越大，则其中包含目标概念的可能性越大，但同时找到某个具体概念的难度也越大，一般假设空间分为有限假设空间与无限假设空间。

12.3 有限假设空间

12.3.1 可分情形

可分情形意味着目标概念$c$属于假设空间$H$。

则对于给定的m个样本的训练集D，如何找出满足误差参数的假设？

由目标概念的定义可知，既然D中的样例都是由目标概念赋予的，并且目标概念存在于假设空间$H$中，那么任何在训练集D上出现标记错误的假设肯定不是目标概念。这样，我们保留下与训练集D的标记保持一致的假设。

显然，只要训练集D足够大，就能最后只保留下一个假设，也就是目标概念的有效近似。

那么，接下来要确定的就是：我们需要这个训练集D有多少示例才能学得目标概念的有效近似？

对于PAC学习来说，只要训练集D的规模能使给定学习算法以概率$1-\delta$找到目标假设的$ϵ$近似即可。

对于包含m个示例的训练集D，h与D表现一致的概率为：


注：泛化误差大于$ϵ$，且在训练集上表现完美的所有假设也就是由于训练集D规模有限而出现的等效假设，将它们出现的概率控制在$\delta$以下（也即式(12.13)所示），就可以保证学习算法以$1-\delta$的概率找到目标假设$c$的近似。

结论：由以上的推论可知，有限假设空间都是PAC可学习的。即：只要样本数目满足式(12.14)，在与训练集一致的假设中总是可以在1-σ概率下找到目标概念的有效近似。

输出假设$h$的泛化误差随样例数目的增多而收敛到0，收敛速率为O($\frac{1}{m}$)

13.3.2 不可分情形

不可分情形指的是目标概念$c$不存在与假设空间$H$。

这时我们就不能像可分情形时那样从假设空间中寻找目标概念的近似。但当假设空间给定时，必然存在一个假设的泛化误差最小，若能找出此假设的有效近似也不失为一个好的目标，这便是不可知学习(agnostic learning)的来源。

这时候便要用到Hoeffding不等式：

则对于假设空间中的所有假设，出现泛化误差与经验误差之差大于$ϵ$的概率和为：

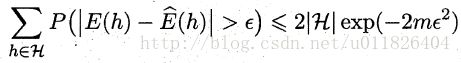
因此，令右边的式子小于等于$\delta$可得满足泛化误差与经验误差相差小于$ϵ$所需的最少样本数，同时也可以求出泛化误差界：

12.4 VC维（无限假设空间）

对于无限假设空间，如实数域中的所有区间、${\mathbb{R}}^d$空间中的所有线性超平面，要对此种情形的可学习性进行研究，需度量假设空间的复杂度。最常见的方法是考虑假设空间的VC维。在介绍VC维之前，需要引入两个概念：

• 增长函数：对于给定数据集D，假设空间中的每个假设都能对数据集的样本赋予标记，因此一个假设对应着一种打标结果，不同假设对D的打标结果可能是相同的，也可能是不同的。随着样本数量m的增大，假设空间对样本集D的打标结果也会增多，增长函数则表示假设空间对m个样本的数据集D打标的最大可能结果数，因此增长函数描述了假设空间的表示能力与复杂度。
  
• 打散：例如对二分类问题来说，m个样本最多有2^m个可能结果，每种可能结果称为一种“对分”，若假设空间能实现数据集D的所有对分，则称数据集能被该假设空间打散。
  
  即：若存在大小为d的示例集能被假设空间打散，但不存在任何大小为d+1的示例集能被假设空间打散，则该假设空间的VC维为d。

VC维和增长函数的关系：

注：(1)式中，假设空间的VC为d，当$m\le d$时，增长函数与$2^m$相等；当m=d时，右边组合数等于$2^d$(被打散)，当m=d+1时，右边等于$2^{d+1}-1$(没打散)
(2)是由(1)推出的

利用增长函数来估计经验误差与泛化误差之间的关系：

将(2)式代入定理12.2就得到：


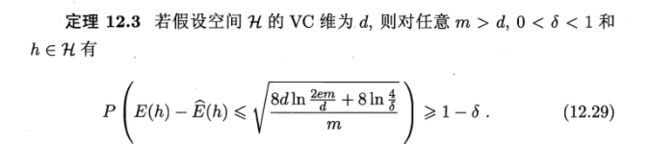
上式给出了基于VC维的泛化误差界，同时也可以计算出满足条件需要的样本数(样本复杂度)。可见，基于VC维的泛化误差界是分布无关、数据独立的，也就是说对任何数据分布都成立。

若学习算法满足经验风险最小化原则（ERM），即学习算法的输出假设h在数据集D上的经验误差最小，可证明：任何VC维有限的假设空间都是（不可知）PAC可学习的，换而言之：若假设空间的最小泛化误差为0即目标概念包含在假设空间中，则是PAC可学习，若最小泛化误差不为0，则称为不可知PAC可学习。

12.5 Rademacher复杂度

基于VC维的泛化误差界由于没有考虑数据本身(分布无关，数据独立)，得到的泛化误差界通常比较“松”。Rademacher复杂度是另一种刻画假设空间复杂度的途径，与VC维不同的是，它在一定程度上考虑了数据分布。

12.6 稳定性

无论是基于VC维还是Rademacher复杂度来推导泛化误差界，所得到的结果均与具体学习算法无关，对所有学习算法都适用。

这使得我们可以脱离具体学习算法的设计来考虑学习问题本身的性质，但在另一方面，若希望获得与算法有关的分析结果，则可以采用稳定性分析。

算法的稳定性分析考察的是算法在输入发生变化时，输出是否会随之发生较大的变化。

算法的均匀稳定性：

若对数据集中的任何样本z，满足：

即原学习器和剔除一个样本后生成的学习器对z的损失之差保持β稳定，称学习器关于损失函数满足β-均匀稳定性。同时若损失函数有上界，即原学习器对任何样本的损失函数不超过M，则有如下定理：

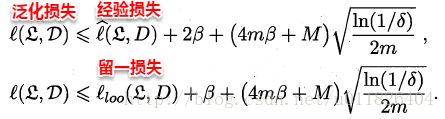
事实上，若学习算法符合经验风险最小化原则（ERM）(即：学习算法输出的假设满足经验损失最小化)且满足β-均匀稳定性，则假设空间是可学习的。

稳定性通过损失函数与假设空间的可学习联系在了一起，区别在于：假设空间关注的是经验误差与泛化误差，需要考虑到所有可能的假设；而稳定性只关注当前的输出假设。