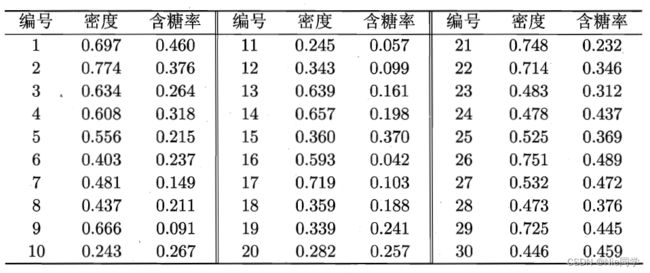
西瓜书学习笔记——密度聚类（公式推导+举例应用）

算法介绍

密度聚类是一种无监督学习的聚类方法，其目标是根据数据点的密度分布将它们分组成不同的簇。与传统的基于距离的聚类方法（如K均值）不同，密度聚类方法不需要预先指定簇的数量，而是通过发现数据点周围的密度高度来确定簇的形状和大小。我们基于DBSCAN算法来实现密度聚类。

DBSCAN是基于一组邻域参数$(ϵ,MinPts)$来刻画样本分布的紧密程度，给定数据集$D=\{x_1,x_2,...,x_m\}$定义以下几个概念：

• $ϵ$-邻域：对$x_j\in D$，其$ϵ$-邻域包含样本集$D$中不大于$ϵ$的样本点，即$N_{ϵ}\left({\mathbf{x}}_j\right)=\left\{{\mathbf{x}}_i\in D\mid \mathrm{dist}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)⩽ϵ\right\}$。
• 核心对象：若$x_j$的$ϵ$-邻域至少包含了$MinPts$个样本，即$\left|N_{ϵ}\left({\mathbf{x}}_j\right)\right|⩾MinPts$，则$x_j$是一个核心对象。
• 密度直达：若$x_j$位于$x_i$的$ϵ$-邻域中，且$x_i$是核心对象，则称$x_j$由$x_i$密度直达。
• 密度可达：对$x_i$与$x_j$，若存在样本序列$p_1,p_2,...,p_n$，其中$p_1=x_i$，$p_n=x_j$且$p_{i+1}$由$p_i$密度直达，则称$x_j$由$x_i$密度可达。
• 密度相连：对$x_i$与$x_j$，若存在$x_k$使得$x_i$与$x_j$均由$x_k$密度可达，则称$x_i$与$x_j$密度相连。
  
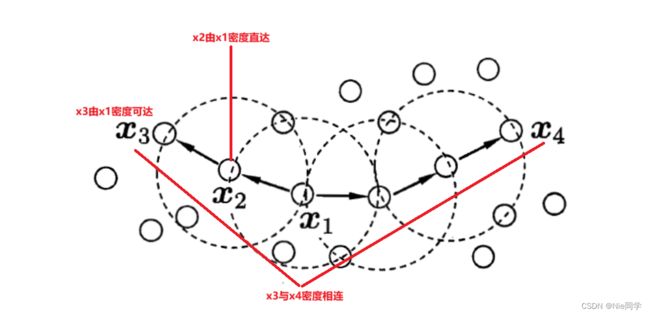
  故DBSCAN算法将簇定义为：由密度可达关系导出的最大密度相连的集合。于是，DBSCAN算法先任选数据集中的一个核心对象为种子，由此出发确定相应的聚类簇，其算法流程图如下所示：

实验分析

数据集如下表所示：

读入数据集：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

data = pd.read_csv('data/4.0.csv')

定义距离函数：

# 定义距离函数
def distance(point1, point2):
    return np.linalg.norm(point1 - point2)

$ϵ$-邻域函数：

# 定义 epsilon-邻域 函数
def epsilon_neighborhood(point, epsilon, data):
    neighbors = []
    for i, other_point in enumerate(data):
        if distance(point, other_point) <= epsilon:
            neighbors.append(i)
    return neighbors

定义核心对象判定函数：

# 定义核心对象判定函数
def is_core_object(point, epsilon, min_pts, data):
    neighbors = epsilon_neighborhood(point, epsilon, data)
    return len(neighbors) >= min_pts

定义 DBSCAN 算法：

def dbscan(data, epsilon, min_pts):
    labels = [0] * len(data)
    cluster_id = 0

    for i, point in enumerate(data):
        if labels[i] != 0:
            continue

        neighbors = epsilon_neighborhood(point, epsilon, data)

        if len(neighbors) < min_pts:
            labels[i] = -1  # 标记为噪声点
            continue

        cluster_id += 1
        labels[i] = cluster_id

        for neighbor in neighbors:
            if labels[neighbor] == -1:
                labels[neighbor] = cluster_id
            if labels[neighbor] != 0:
                continue

            labels[neighbor] = cluster_id
            other_neighbors = epsilon_neighborhood(data[neighbor], epsilon, data)

            if len(other_neighbors) >= min_pts:
                neighbors.extend(other_neighbors)

    return labels

设置超参数：

# 设置 epsilon 和 min_pts 参数
epsilon_value = 0.1
min_pts_value = 4

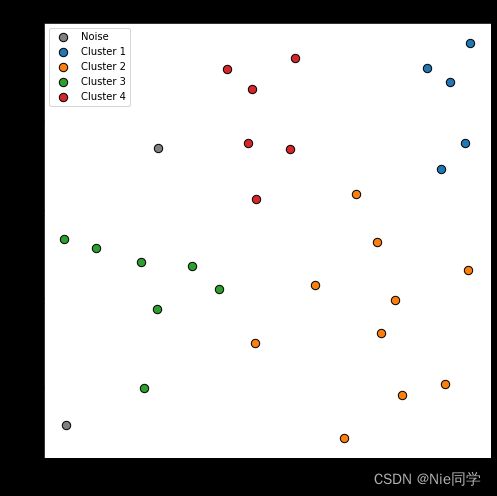
执行DBSCAN算法并绘制结果：

# 执行 DBSCAN 算法
result_labels = dbscan(data.to_numpy(), epsilon_value, min_pts_value)

# 获取唯一的聚类标签
unique_labels = np.unique(result_labels)

# 绘制结果
plt.figure(figsize=(8, 8))
for label in unique_labels:
    if label == -1:
        plt.scatter(data['Density'][result_labels == label], data['Sugar inclusion rate'][result_labels == label], 
                    c='gray', marker='o', edgecolors='black', s=70, label='Noise')
    else:
        plt.scatter(data['Density'][result_labels == label], data['Sugar inclusion rate'][result_labels == label], 
                    label=f'Cluster {label}', marker='o', edgecolors='black', s=70)

plt.title('DBSCAN Clustering Result')
plt.xlabel('Density')
plt.ylabel('Sugar inclusion rate')
plt.legend()
plt.show()