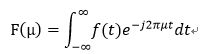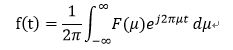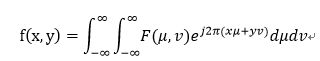频率域滤波

之前介绍了关于空间域滤波的一些操作，主要目的是减少噪声和平滑图像，空间域的处理方法都是在已知噪声数据类型基础上进行噪声过滤的，而在某些噪声图像类别上上述方法就显得十分渺小了，频率域的引入就是来寻找噪声的类型，并进行空间过滤的。其中频率是单位时间变化期间，一个周期函数重复相同值序列的次数。频率域滤波(即波数)为图像像元的灰度值随着位置变化的空间频率，以频谱表示信息分布特征，可以将一幅图像像元值在空间上的变化分解为 具有不同振幅、空间频率和相位的简振函数的线性叠加，图像中各种空间频率成分的组成和分布称为空间频谱。这种对图像的空间频率特征进行分解、处理和分析称为频率域处理。频率中最典型的就是傅立叶变换，傅立叶变换能把图像从空间域变换到只包含不同频率信息的频率域，原图像上的灰度突变部位、图像结构复杂的区域、图像细节及干扰噪声等信息集中在高频区，而原图像上灰度变化平缓部位的信息集中在低频区(变换函数还有小波变换，将在后续进行分析和解析)。

傅立叶变换

傅立叶变换是将时间域转换为频率域的工具，傅立叶指出任何周期或函数都可以表示为不同频率的正弦和/或余弦之和的形式，每个正弦和/或余弦乘以不同的系数（称该和为傅立叶级数）。无论函数多么复杂，只要它是周期的，并且满足一定条件，都可以用这样的和表示。一维变换函数（一对，变换及反变化函数）为：

其中，变换后的的函数F(x)，f(t)为变换前周期函数，μ为周期函数分量，周期从0到1/2π。

利用一维变量扩展到二维变量，二维傅立叶变换公式为：

e^j2π(xμ+yv)实际上是一个平面波（的共轭），它的传播方向与(u,v)相同，角频率是 根号下x^2+y^2。可以看做是平面波在x方向的角频率是u和y方向的角频率是v。二维傅立叶变换具有旋转不变性了（证明：如何证明二维离散傅里叶变换的旋转不变性？）。同时，变换完，中心是两个角频率都为0（直流分量），越靠近中心，两个方向的角频率越低，合成的角频率与到中心的距离成正比，所以中心是低频分量，外部是高频分量。幅度决定图像的强弱，相位觉得图像的像素。分析

频率域滤波基本步骤

preprocessing：图像预处理步骤，用0填充f(x,y)，在二维循环卷积时为了保证周期性进行0填充（傅里叶变换滤波时，为什么需要对输入数据进行零填充？）

Fourier transform：图像傅立叶变换

filter function：滤波器

Inverse Fourier transform：反向傅立叶变换

postprocessing：图像裁剪，输出g(x,y)

伪流程：

1.f(x,y)是由MxN构成，填充图像大小为P(P=2M)xQ(Q=2N)，f_p(x,y)

2.将f_p(x,y)利用-1^(x+y)将图片滤波器移动到中心，低频部分移到中间，高频部分移到四周，以便后面的计算。

3.计算f_p(x,y)傅立叶变化得到F(u,v)

4.生成一个实的、对阵的过滤器，中心在（P/2,Q/2），大小为PxQ

5.计算H(u,v)F(u,v)，并进行换位，得到初始时图像的傅立叶变换（DEF）的数据排列形式，即低频部分在四周，高频部分在中间（原点在左上角意味着低频部分在左上角，又因为的DEF是中心对称的，可得初始时图像的DEF应是低频在四周高频在中间）。

6.计算反傅立叶函数，得到每个元素的幅度（实部和虚部平方和的平方根），并取左上角MxN区域，得到最终的输出图像g(x,y)。

过滤器

将一幅图像的模糊化（频率域平滑）可通过高频的衰减来达到，称为低通滤波器。

将一幅图像的锐利化（边缘聚变与高频有关）可通过低频的衰减来达到，称为高通滤波器。

a.低通滤波器

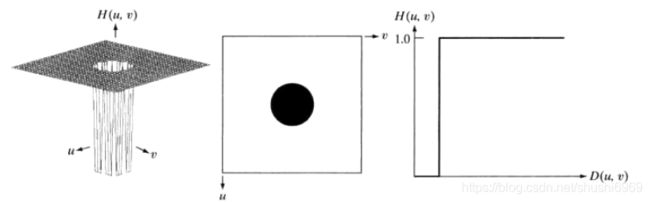
（1）理想低通滤波器

在以原点为圆心，以为半径的园内，无衰减地通过所有频率，而在该圆外"切断"所有频率的二维低通滤波器，称为理想低通滤波器，它由下面函数确定：

其中，D(u,v)是频率域中点(u,v)与频率矩阵中心的距离，即：

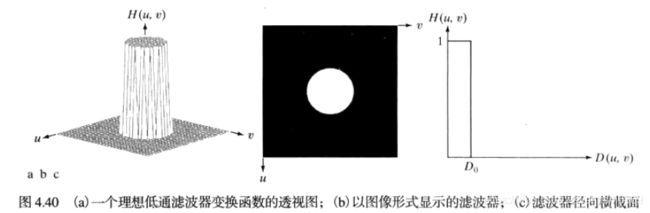
图4.40(a)中是H(u,v)的透视图，图b显示了以图像显示的滤波器，表明在半径D0的圆内，所有频率都无衰减的通过，而在此圆外的所有频率则是完全被衰减（滤除）。理想低通滤波器是关于原点径向对称的，这意味着该滤波器完全是一个径向横截面来定义，将图绕着H(u,v) 360度旋转则得到图a。

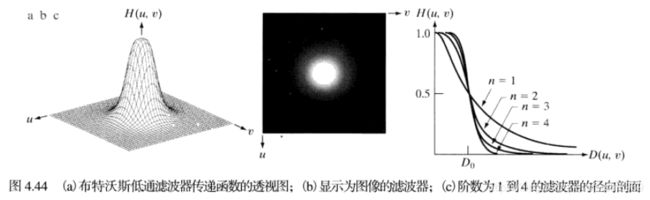
（2）布特沃斯低通滤波器

截止频率位于距原点D0处的n阶布特沃斯低通滤波器（BLPF）的传递函数定义如下：

BLPF传递函数并没有在通过频率和滤除频率之间给出明显截止的尖锐的不连续性。图4.44(a)是透视图，表明在半径D0的圆内，频率是有规则的通过，而在此圆外的所有频率则是完全被衰减（滤除）。在空间域的一阶布特沃斯滤波器没有振铃现象，在二阶滤波器中，振铃现象通过很难察觉（通过设置不同的n值，二阶的BLPF是在有效的低通滤波和可接受的振铃特性之间好的折中），单更高阶数的滤波器中振铃现象会很明显。

（3）高斯低通滤波器

二维高斯低通滤波器（GLPF）形式如下：

其中D(u,v)是距离频率矩形中心的距离，是关于中心扩展度的度量。图4.47显示了一个GLPF函数的透视图、图像显示和径向剖面图。GLPF的傅立叶反变换也是高斯的，从图a看得到的空间高斯滤波器没有振铃。

b.高通滤波器

通过衰减图像的傅立叶变换的高频成分可以平滑图像。因为边缘和其他灰度的急剧变化与高频分量有关，所以图像的锐化可在频率域通过高通滤波来实现，高通滤波会衰减傅立叶变换中的低频分量而不会扰乱高频信息。

（1）理想高通滤波器

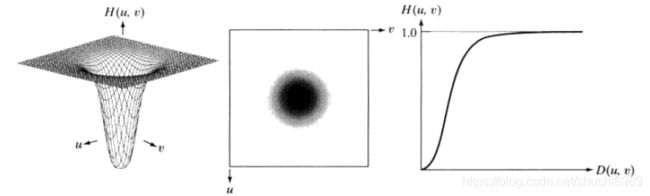
一个二维理想高通滤波器（IHPF）定义为

其中是截止频率，D(u,v)是频率域中点(u,v)与频率矩阵中心的距离。在这种滤波器下，IHPF把以半径为的圆内的所有频率置0，而毫无衰减地通过圆外的所有频率。和理想低通过滤器完全相反。下图为理想高通滤波器的透视图、图像表示和剖面图。

（2）布特沃斯高通滤波器

截止频率的n阶布特沃斯高通滤波器(BHPF)定义为：

类似于低通滤波器，BHPF比IHPF更平滑一些。下图为布特沃斯高通滤波器的透视图、图像表示和剖面图。

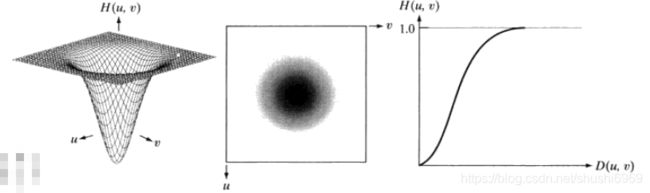
（3）高斯高通滤波器

截止频率出在距频率矩形中心距离为的高斯高通滤波器(GHPF)的传递函数：

类似高斯低通滤波器，高斯高通滤波器比理想高通滤波器、布特沃斯高通滤波器平滑效果更好一些。即使是对微小物体和细线条使用高斯滤波器滤波，结果也是比较清晰的。下图为高斯高通滤波器的透视图、图像表示和剖面图。

 

https://www.cnblogs.com/laumians-notes/p/8544256.html

https://blog.csdn.net/liuweiyuxiang/article/details/77040942

https://blog.csdn.net/nanhuaibeian/article/details/90738701

https://blog.csdn.net/chanxiaogang/article/details/45226373

https://blog.csdn.net/eeeee123456/article/details/82950986