图像直方图均衡化和空间滤波

直方图均衡化和空间滤波

---

1习题

1.1 直方图均衡化

假设你对一张图已经进行了一次直方图均衡化的操作。如果对这张图进行第二次直方图均衡化，得到的结果跟第一次均衡化的结果一样吗？请给予证明。

直方图均衡化处理是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布，就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。它的基本思想是对图像中像素个数多的灰度级进行展宽，而对图像中像素个数少的灰度进行压缩，从而扩展像原取值的动态范围。

L为图像灰度级， Pr(rj) 表示原始灰度值 rj 对应出现的概率，直方图均衡化公式：

sk=T(rk)=(L−1)∑j=0kPr(rj)

=(L−1)MN∑j=0knj

k=0,1,2...,L−1

rj 对应的像素灰度经过直方图均衡化后变为 sk ，所以变的是对应的灰度级，而对应灰度级的累积分布概率积分CDF不变，让 Ps(rj) 表示直方图均衡化后灰度值 rj 对应出现的概率,则有；

∑j=0kPr(rj)=∑j=0kPs(rj)

k=0,1,2,,⋯,L−1

所以由直方图均衡化变化的原理可以得出结论，对图片第二次直方图均衡化之后的变换函数跟第一次直方图均衡化结果一样，直方图均衡化结果也相同。

1.2 空间滤波

给定一张 4 x 4 的灰度图和一个 3 x 3 的滤波器：
图像:

⎡⎣⎢⎢⎢85169181213815534202431635080204480⎤⎦⎥⎥⎥

滤波器：

⎡⎣⎢10−110−110−1⎤⎦⎥

1. 用给定的滤波器对这张灰度图（边界补零）进行卷积，写出卷积后的结果（大小应为 4 x
   4）。

⎡⎣⎢⎢⎢17775−131−173420218−324−336271249−107−362263107−133−207⎤⎦⎥⎥⎥

1. 请说出你得到的卷积结果中正数和负数分别表示什么含义。

正数表示从垂直方向由上往下灰度值递减，负数表示从垂直方向由上往下灰度值递曾，即看绝对值。

1. 根据你所学到的知识， 谈一谈题目中给出的 3 x 3 滤波器可以有哪些应用。

可做水平匹配滤波边缘检测

---

2编程题

2.1直方图均衡化

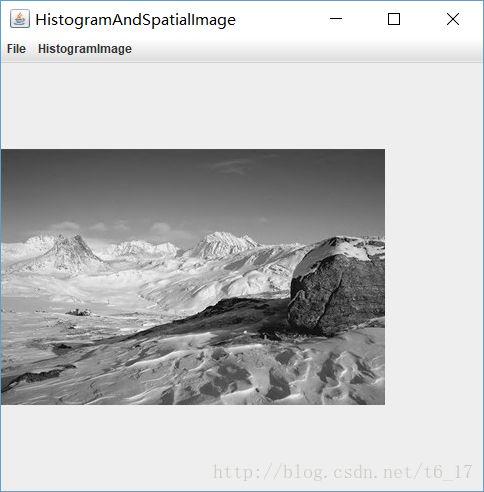
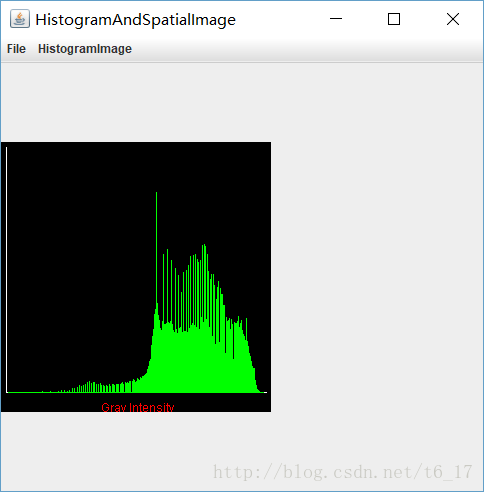
1. 计算并显示图像的直方图， 并把结果粘贴到报告里。注意：你必须用你自己实现的函数
   来计算直方图，但是允许调用现成的 API 来显示直方图。 (例如，你不能调用 Matlab 的“imhist”
   来计算直方图，但是可以调用“subplot” , “hist”来显示直方图。 )

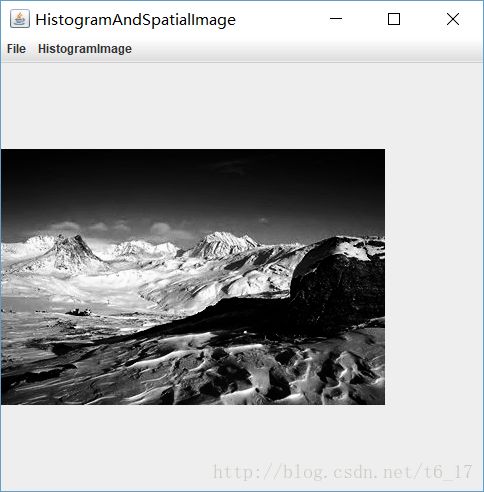
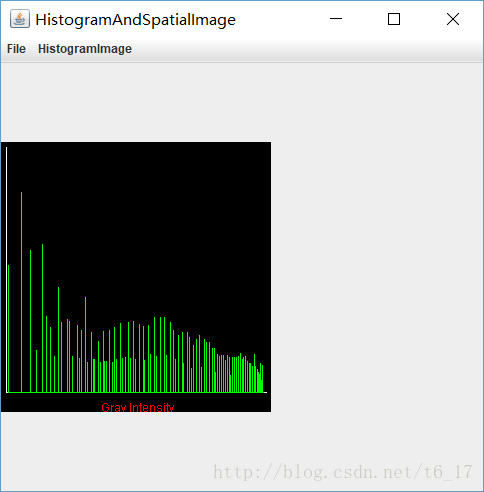
进行直方图均衡化，将均衡化后的结果和相应的直方图粘贴到报告里。

1. 分析直方图均衡化后的结果，字数不能超过一页。

直方图均衡化处理之后，原来比较少像素的灰度会被分配到别的灰度去，像素相对集中， 处理后灰度范围变大，对比度变大，清晰度变大，所以能有效增强图像。
原图中灰度强的点比较多，所以直方图均衡化后，分布在灰度弱的点也比较多。

3.详细描述你是如何实现直方图均衡化操作的，也就是说，针对“equalize_hist”函数进
行算法说明，字数不能超过两页。请集中在算法描述方面，不要过多地复制/粘贴代码到报告上。

直方图均衡化遵循上面的公式

(L−1)MN∑j=0knj

先计算出图像中每个的的灰度级的点数，然后求CDF，在将原来点灰度级别重新分配。

直方图均衡化主要代码

    double k = (double)255 / (double)(height * width);
    double[] c = new double[256];
    c[0] = k * array[0];
    for (int i = 1; i < 256; i++) {
      c[i] = c[i - 1] + k * array[i];
    }

2.2空间滤波

1. 分别用 3 x 3， 7 x 7 和 11 x 11 的均值滤波器来平滑你输入的图像，将相应的三个输出结
   果粘贴到报告里。

3×3

7×7

11×11

2.用 3 x 3 的拉普拉斯滤波器来锐化你输入的图像（课本上有 4 种拉普拉斯滤波器，参见图
3.37， 你可以使用其中任意一种），并将输出结果放在报告中。除此之外，请简单介绍一下为什
么拉普拉斯滤波器可以用于图像的锐化。

使用矩阵进行拉普拉斯变换

⎡⎣⎢0101−41010⎤⎦⎥

实验结果：

拉普拉斯锐化图像是根据图像某个像素的周围像素到此像素的突变程度有关，也就是说它的依据是图像像素的变化程度。我们知道，一个函数的一阶微分描述了函数图像是朝哪里变化的，即增长或者降低；而二阶微分描述的则是图像变化的速度，急剧增长下降还是平缓的增长下降。
当邻域中心像素灰度低于它所在的领域内其它像素的平均灰度时，此中心像素的灰度应被进一步降低，当邻域中心像素灰度高于它所在的邻域内其它像素的平均灰度时，此中心像素的灰度应被进一步提高，以此实现图像的锐化处理。

---

3.将高提升滤波（high-boost filter） 用在输入的图像中 （也就是说， g(x,y)=f(x,y)+k∗gmax(x,y) 其他细节参见课本式(3.6-9)）。过程中涉及的平滑部分应用用课本图 3.32(a)所示的滤波器来完成。请自行选择合适的 k（式(3.6-9)中的权值）。在报告中，你需要说明你选择的 k的值，并贴上对应的输出结果。

我们选择k=2
实验结果：

1. 详细描述你是如何实现空间滤波操作的，也就是说，针对“filter2d”函数进行算法说
   明，字数不能超过两页。

g(x,y)=∑s=−aa∑t=−bbw(s,t)w(s,t)f(x+s,y+t)

用滤波矩阵对图像矩阵进行卷积操作，滤波变换原图像的点数不变，控制好边缘的点对应相乘相加。
关键代码：

public int[][] getFilteringArray(int[][] imageArray, int[][] filteringArray) {
    int height = imageArray.length, width = imageArray[0].length;
    int[][] temp = new int[height][width];
    for (int i = 0; i < height; i++) {
      for (int j = 0; j < width; j++) {
        temp[i][j] = getFilteringValue(i, j, imageArray, filteringArray);
      }
    }
    return temp;
}

public int getFilteringValue(int row, int col, int[][] imageArray, int[][] filteringArray) {
    int count = 0;
    int height = imageArray.length, width = imageArray[0].length;
    int filterLength = filteringArray.length;
    int gap = (filterLength - 1) / 2;
    for (int i = 0; i < filterLength; i++) {
      for (int j = 0; j < filterLength; j++) {
        if (row + i - gap >= 0 && row + i - gap < height && 
          col + j - gap >= 0 && col + j - gap < width) {
          count += imageArray[row + i - gap][col + j - gap];
        }
      }
    }
    return count / (filterLength * filterLength);
}

将完整代码放在github上了，需要的可以参考。