经典论文解析——MobileNet系列
MobileNet系列
- V1—MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
- 1. 简介
- 2. 网络介绍
- 2.1 深度可分离卷积(Depthwise Separable Convolution)
- 2.2 网络结构
- 2.3 超参数1——Width Multiplier α
- 2.4 超参数2——Resolution Multiplier ρ
- 3. 实验
- 4. 补充知识
- V2—MobileNetV2: Inverted Residuals and Linear Bottlenecks
- 1. 简介
- 2. 网络介绍
- 2.1 线性瓶颈层(Linear Bottlenecks)
- 2.2 Inverted Residuals
- 2.3 网络结构
- 3. 实验结果
- V3—Searching for MobileNetV3
- 1.简介
- 2. 网络结构搜索与优化(NAS, NetAdapt)
- 3. 网络介绍
- 3.1 重新设计网络前端和末端
- 3.2 非线性激活层
- 3.3 在基础模块中增加SE注意力模块
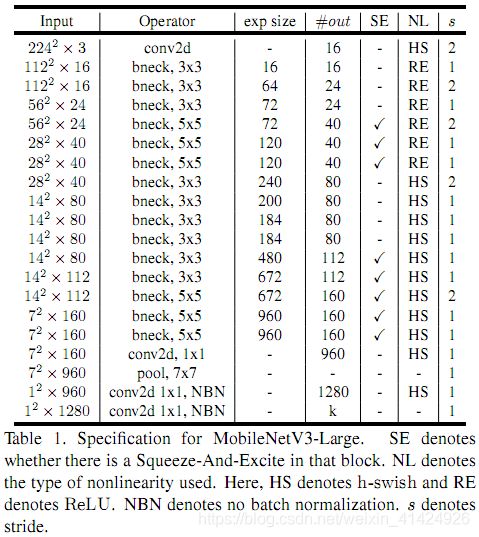
- 3.4 网络结构——Large版和Small版
- 4.实验结果
本博文中绝大部分图片均来自MobileNet系列论文原图。文中如有错误,或您有不同的看法,请评论中指出讨论,谢谢。
V1—MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
1. 简介
- 作者设置了两个超参数 α , ρ α,ρ α,ρ,可以很方便地在网络效率和精度之间进行平衡;
- 作者巧妙利用了深度可分离卷积来替换普通卷积;
2. 网络介绍
2.1 深度可分离卷积(Depthwise Separable Convolution)
深度可分离卷积就是对于输入张量的每一层通道,都单独应用一个卷积核。所以张量每层应用的卷积核的参数都不相同。这个过程叫做"depthwise convolutions"。然后,再用普通的1×1卷积层将张量所有通道的信息进行整合,并将张量的通道数调整为设置好的数值。这个过程叫做"pointwise convolution"。(普通卷积则是每层通道应用的卷积核的参数都相同,并且通道间的信息整合和每层通道空间方向的信息提取是同时完成的)。depthwise convolution和pointwise convolution之后都有BN层和ReLU非线性激活层。
深度可分离卷积可以很大程度上降低计算量和网络的大小。假设输入张量尺寸为 D F × D F × M D_F\times D_F\times M DF×DF×M,设定的输出张量尺寸为 D F × D F × N D_F\times D_F \times N DF×DF×N,卷积核大小为 K × K K\times K K×K,那么该卷积层的总参数数量即为:
参 数 数 量 { 普 通 卷 积 层 : K × K × M × N 深 度 可 分 离 卷 积 层 : K × K × M + 1 × 1 × M × N 参数数量\begin{cases}普通卷积层:K\times K\times M\times N \\深度可分离卷积层:K\times K\times M+1\times 1\times M\times N\end{cases} 参数数量{普通卷积层:K×K×M×N深度可分离卷积层:K×K×M+1×1×M×N
计 算 量 { 普 通 卷 积 层 : K × K × M × N × D F × D F 深 度 可 分 离 卷 积 层 : ( K × K × M + 1 × 1 × M × N ) × D F × D F 计算量\begin{cases}普通卷积层:K\times K\times M\times N\times D_F\times D_F \\深度可分离卷积层:(K\times K\times M+1\times 1\times M\times N)\times D_F\times D_F\end{cases} 计算量{普通卷积层:K×K×M×N×DF×DF深度可分离卷积层:(K×K×M+1×1×M×N)×DF×DF
深 度 可 分 离 卷 积 参 数 量 普 通 卷 积 参 数 量 = K × K × M + 1 × 1 × M × N K × K × M × N = 1 N + 1 K 2 \frac{深度可分离卷积参数量}{普通卷积参数量}=\frac{K\times K\times M+1\times 1\times M\times N}{K\times K\times M\times N }=\frac{1}{N}+\frac{1}{K^2} 普通卷积参数量深度可分离卷积参数量=K×K×M×NK×K×M+1×1×M×N=N1+K21
从上述公式可以看出,深度可分离卷积层参数量更少,网络的大小也就相应减少;另外,计算量也相应减少,网络的效率也就更高。那么精度的改变如何呢?作者经过试验证明了,将普通卷积层换成深度可分离卷积层后,只损失了少量的精度。
2.2 网络结构
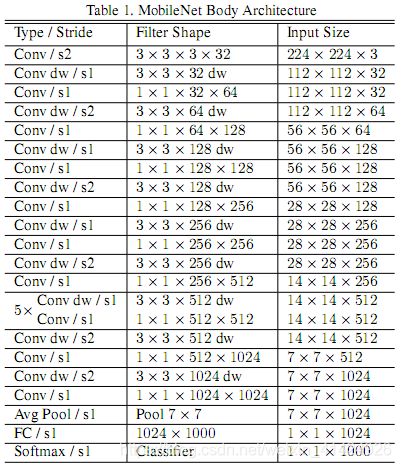
MobileNet除了第一层是普通卷积层外,其他都是深度可分离卷积层。除了最后的全连接层没有ReLU层外,每个网络层后都有BN层和ReLU非线性激活层。最后的全连接层后接softmax层进行分类。网络的下采样是使用带步长的卷积层来实现的。最后,在全连接层前,使用了全局池化将张量的尺寸变为1×1。
优化器采用RMSprop,并且由于MobileNet旨在设计轻量级网络,因此不使用正则化和数据增广,小网络通常不会过拟合。作者发现,对于depthwise convolution中的卷积核,不设置权重衰减是很重要的,因为这些卷积核里参数非常少。
作者提到,仅仅将网络理论上的Mult-Adds数量大大减少是不够的。还需要确保硬件实施的时候是可行的。比如,未结构化的稀疏矩阵的计算并不会比稠密矩阵快很多,除非稀疏等级非常高。作者设计的网络将绝大多数的计算量都投入到了1×1卷积层里,也就是pointwise convolution。这可以利用优化的**通用矩阵乘法(GEMM)**来实现。而1×1卷积层可以省略im2col的映射操作,直接使用GEMM进行计算,因此提高了网络的效率。下图可以看到,通过这种MobileNet的网络设计后,网络的Mult-Add大部分都集中在1×1卷积层中,这类卷积层也具有约75%的参数量,其余参数量几乎都分布在全连接层中。
2.3 超参数1——Width Multiplier α
其实就是将网络里所有的输入输出通道全部缩减 α \alpha α倍( α ∈ ( 0 , 1 ] \alpha\in(0,1] α∈(0,1])。论文中作者实验设计 α = 1 , 0.75.0.5 , 0.25 \alpha=1,0.75.0.5,0.25 α=1,0.75.0.5,0.25。从上文的参数量计算公式可以看出,网络参数的减少大致与 α 2 \alpha^2 α2成正比。
K × K × M + M × N ⇒ K × K × α M + α M × α N K\times K\times M+M\times N\Rightarrow K\times K\times\alpha M+\alpha M\times\alpha N K×K×M+M×N⇒K×K×αM+αM×αN
2.4 超参数2——Resolution Multiplier ρ
其实就是减少网络输入图像的分辨率,作者实验设置了224,192,160和128四个分辨率等级,分辨率224×224的图像对应的 ρ = 1 ρ=1 ρ=1。降低输入图像的分辨率并不会减少网络参数,但是会减少网络的计算量。同样,计算量的减少大致与 ρ 2 ρ^2 ρ2成正比。
( K × K × M + × M × N ) × D F × D F ⇒ ( K × K × M + × M × N ) × ρ D F × ρ D F (K\times K\times M+\times M\times N)\times D_F\times D_F \Rightarrow (K\times K\times M+\times M\times N)\times ρD_F\times ρD_F (K×K×M+×M×N)×DF×DF⇒(K×K×M+×M×N)×ρDF×ρDF
3. 实验
4. 补充知识
什么是通用矩阵乘法(General Matrix Multiply)?什么是im2col操作?
GEMM是深度学习中极其重要的算法,全连接层和卷积层的底层实现基本上都是靠这个算法完成的。简单来说,GEMM就是将高维的张量映射为二维的矩阵,然后再进行计算,可以大大提高计算效率。另外,高维数据在计算机内部的储存通常是非连续的,而二维数据在计算机内部的储存可以是成片连续的,因此访问数据的效率也更高。那么要怎么将高维张量映射为二维矩阵呢?
假设张量尺寸为 H × W × C I H\times W\times C_I H×W×CI,设置的输出张量为 H × W × C O H\times W\times C_O H×W×CO,卷积核尺寸为 K × K × C I K\times K\times C_I K×K×CI,个数为 C O C_O CO个。那么将卷积核按特定步长扫过整个张量,每移动一次,就将卷积核覆盖的张量 K × K × C I K\times K\times C_I K×K×CI摊平,变为一个行向量。这样,通过适当的Padding,我们就可以得到一个行为 H × W H\times W H×W,列为 K × K × C I K\times K\times C_I K×K×CI的矩阵 M t e n s o r M_{tensor} Mtensor。同理,我们将 C O C_O CO个卷积核摊平,按列堆叠,就可以得到一个行为 K × K × C I K\times K\times C_I K×K×CI,列为 C O C_O CO的矩阵 M k e r n e l M_{kernel} Mkernel。上述的转换过程就是im2col操作的效果。这样,我们就可以将两个矩阵相乘而得到结果。
M t e n s o r × M k e r n e l = M o u t p u t { ( H × W ) × C O ) } M_{tensor}\times M_{kernel}=M_{output}\{(H\times W)\times C_O)\} Mtensor×Mkernel=Moutput{(H×W)×CO)}


V2—MobileNetV2: Inverted Residuals and Linear Bottlenecks
1. 简介
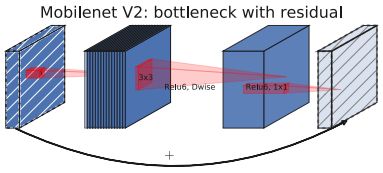
- 作者提出了Inverted Residual bottleneck(倒残差瓶颈模块)。和普通残差bottleneck模块不同,该模块的输入是低维特征张量,然后先经过升维,再经过depthwise convolution,最后再用线性卷积层恢复为低维张量(普通bottleneck是先降维,减少计算量,再升维)。由于中间使用depthwise convolution,其参数量较少,所以即使是升维再卷积,也不会增加很多参数。另外,线性卷积层的意思是,通过卷积降维后,不使用非线性激活层。具体原因见后文。
- 作者说明了ReLU等非线性激活层对于网络中信息流的影响,对于低维特征,ReLU很容易造成信息坍塌。对于高维特征,则可以保存更多信息。
- 相比于MobileNetV1,其实作者是将网络的基本模块从depthwise seperable convolution转换成了Inverted Residual Linear bottleneck Block,其实就是在depthwise seperable convolution的基础上,增加了Inverted Residual和Linear Bottleneck思想。
2. 网络介绍
2.1 线性瓶颈层(Linear Bottlenecks)
作者文中说,网络所有层的激活张量的集合一起构造了一个叫做“manifold of interest"的东西。
为了助于理解,搜了一下manifold的英文翻译,其中有一个是“a set of points such as those of a closed surface or an analogue in three or more dimensions”,所以我感觉manifold of interest可以理解为包含所有特征点的一个多维空间内的封闭曲面。
由于这段在论文中较难理解,以下给出原文和我自己理解后的翻译:
“It has been long assumed that manifolds of interest in neural networks could be embedded in low-dimensional subspaces. In other words, when we look at all individual d-channel pixels of a deep convolutional layer, the information encoded in those values actually lie in some manifold, which in turn is embeddable into a low-dimensional subspace. ”
长期以来,人们一直认为神经网络中包含所有特征的高维空间可以压缩成低维子空间。换句话说,一个卷积层激活张量中,每个蕴含了已编码信息的d维像素值(特征图每个像素都有d个通道),都应该落在某个高维曲面内,而这个高维曲面可以转换为低维子空间。
“At a first glance, such a fact could then be captured and exploited by simply reducing the dimensionality of a layer thus reducing the dimensionality of the operating space. This has been successfully exploited by MobileNetV1 [27] to effectively trade off between computation and accuracy via a width multiplier parameter, and has been incorporated into efficient model designs of other networks as well [20]. Following that intuition, the width multiplier approach allows one to reduce the dimensionality of the activation space until the manifold of interest spans this entire space. However, this intuition breaks down when we recall that deep convolutional neural networks actually have non-linear per coordinate transformations, such as ReLU. For example, ReLU applied to a line in 1D space produces a ’ray’, where as inRn space, it generally results in a piece-wise linear curve with n-joints.”
乍看之下,我们可以直接通过减少每一层的通道数或减少操作空间的维度来获取和应用上述事实。MobileNetV1就是个很好的例子,它利用超参数width multiplier α \alpha α来减少网络层的通道数,从而提高网络效率。只要 α \alpha α不让网络的特征空间维度小于理论的manifold of interest,网络就能保持原有的效果。但是,由于ReLU等非线性激活层的存在,上述的空间转换就会出现问题。比如说,ReLU应用在1维空间的一条线上,会产生射线;应用在n维空间则会产生具有n个接头的分段曲线。

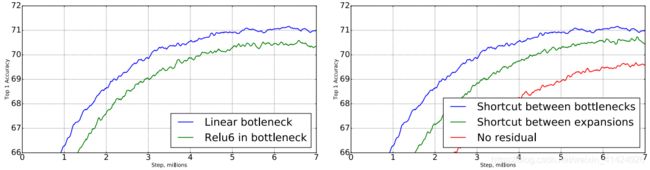
上图说明,输入一个螺旋形的张量,在经过矩阵变换和ReLU激活后,如果输出维度越低,那么损失的信息越多。而输出维度越高,则保存的信息越多。因此,作者将张量维度较低网络层的非线性激活都取消了,而保留维度较高网络的非线性激活层。具体见2.2节。
2.2 Inverted Residuals

论文的图3显示了普通残差模块和倒残差模块的区别,直观上,好像是倒残差模块的输入先进行了升维,再降维,且斜线的卷积层没有非线性激活;而普通残差模块正好相反。但是其背后的设计思想则是如下:
通过上述2.1分析可知,其实在普通的残差模块中,信息先经过降维压缩后,仍然保存着所有需要的信息(仍然处于manifold of interest内),而后续的升维扩展以及伴随的非线性激活都只是细节的补充。所以,作者改变残差模块的连接对象,将残差模块中压缩后的张量连接起来。这样,不仅可以保证梯度反向传导,还能节省大量计算时间,因为压缩后的张量的相加计算量更少。

和MobileNetV1的depthwise seperable convolution相比,MobileNetV2的Inverted residual block多了一个1×1卷积层。但是由于两个版本网络的特性不同,所以V2版本输入模块的通道数相比于V1来说要小很多,因此效率也更高。Inverted residual block的计算量为:
( M × t M + K × K × M + 1 × 1 × t M × N ) × D F × D F (M\times tM+K\times K\times M+1\times 1\times tM\times N)\times D_F\times D_F (M×tM+K×K×M+1×1×tM×N)×DF×DF
其中,t是通道的扩张系数。
2.3 网络结构

网络具体结构如上。除了第一个bottleneck模块,其他模块的扩张系数都是6,因为作者实验发现系数在5-10之间效果都差不多。同MobileNetV1,作者还是使用两个超参数来平衡网络速度和精度。但有一点不同,作者发现对于小网络来说,最后一层的通道数不随width multiplier改变的话,效果更好。下图是不同步长的bottleneck模块的结构图。

3. 实验结果
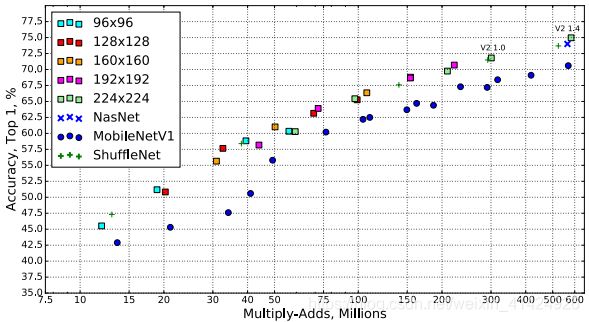
不同网络和不同分辨率的对比结果如下图:

Linear Bottleneck思想的实验验证(下左图)以及Inversed Residual思想的验证(下右图)

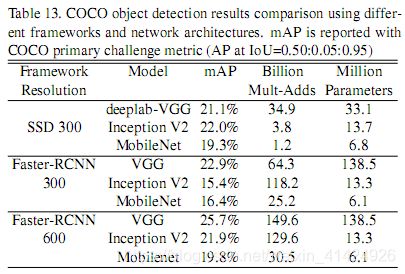
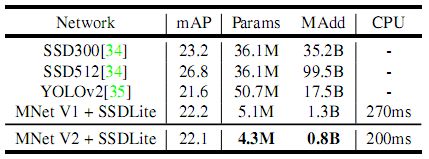
针对COCO数据集,不同目标检测网络结果的对比:
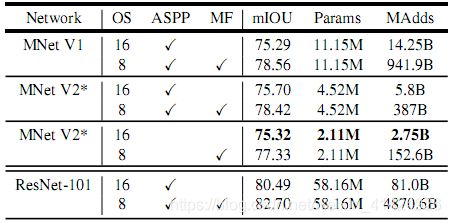
基于DeepLabV3的图像语义分割结果对比(不同backbone):
V3—Searching for MobileNetV3
1.简介
- 网络的设计不再是人为设定了,而是先采用NAS算法,计算出大体的网络结构,然后再使用NetAdapt算法优化每个层的输入输出通道数。从而通过算法得到一个网络效率在设定目标时间内的“最优"网络结构。这是本篇论文最重要的部分之一;
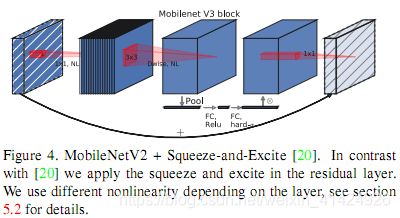
- MobileNetV3的基础模块是在MobileNetV2的bottleneck模块的基础上,增加SE注意力模块得到的。
- 作者还提出了h-swish激活函数,相比于swish激活函数(swish=x·sigmoid(x)),h-swish激活函数就是使用ReLU6(x+3)/6来近似替代sigmoid函数,从而使该激活函数能在任何软硬件平台应用,并提高计算效率。
2. 网络结构搜索与优化(NAS, NetAdapt)
暂时略
3. 网络介绍
3.1 重新设计网络前端和末端
 由于网络的前几层和最后几层是消耗计算资源最多的层,所以作者对其进行了优化。对于网络第一层,作者实验证明网络通道数可以从32修改为16,并将激活函数改为h-swish。这样节省了大约3ms时间。
由于网络的前几层和最后几层是消耗计算资源最多的层,所以作者对其进行了优化。对于网络第一层,作者实验证明网络通道数可以从32修改为16,并将激活函数改为h-swish。这样节省了大约3ms时间。
对于网络的输出端,作者将原来全局池化前的1×1卷积层放在全局池化后,该卷积层本来的目的是对数据进行升维,以便得到更好的预测效果,但是会大大提高计算量。经过这么操作后,前面一个bottleneck模块只需要保留第一个1×1卷积层即可,实验证明这并不影响精度,还将网络速度提高了7ms。(感觉就是删掉了最后一个bottleneck模块,再在全局池化后多加一个1x1卷积层…)
3.2 非线性激活层
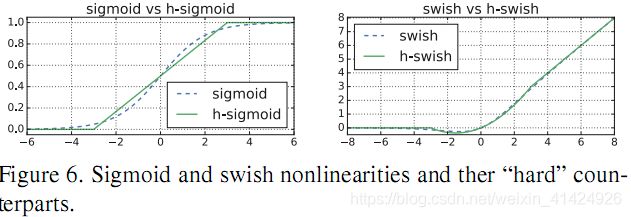 作者引入了一种新的非线性激活函数swish,并将其进行了改善,改成了h-swish(都是自家产品),两者差别如上图,公式如下:
作者引入了一种新的非线性激活函数swish,并将其进行了改善,改成了h-swish(都是自家产品),两者差别如上图,公式如下:
{ s w i s h ( x ) = x ⋅ σ ( x ) h − s w i s h ( x ) = x ⋅ R e L U 6 ( x + 3 ) 6 \begin{cases}swish(x)=x·\sigma(x)\\h-swish(x)=x·\frac{ReLU6(x+3)}{6}\end{cases} {swish(x)=x⋅σ(x)h−swish(x)=x⋅6ReLU6(x+3)
作者发现这种改变对网络效果没有影响,而用ReLU近似sigmoid可以使该激活函数应用在任意移动平台上,并且在量化模式时具有更高的效率。此外,非线性激活层计算量的增加对深层网络效率的影响较小,因为深层网络的张量元素较少。作者在实验时还发现,h-swish对网络的增益大多发生在网络深层,因此作者只在后半部分网络使用了h-swish,前半部分仍然使用ReLU(除了第一层外)。
3.3 在基础模块中增加SE注意力模块
上面的是MobilenetV2的基本模块,下面的是加入了SE注意力模块后的V3版本的基础模块。为了减少增加SE模块所带来的计算量增长的影响,作者将所有SE模块的通道数都设置为扩张通道的数目的1/4。这样既增加了精度,又不影响网络效率。