【计算机视觉】基础矩阵

---

一、外极几何

用两个相机在不同位置拍摄同一物体，两张照片中的景物有重叠部分，那么理论上这两张照片会存在一定的对应关系即外极几何。

外极几何示意图：

在上图中，PO₁O₂为极平面，O₁、O₂分别为相机的中心点，P为空间中一点，P在图像平面上的投影分别为p₁、p₂，照相机中心之间的基线O₁和O₂与图像平面交于外极点e₁、e₂。
而对极几何则是描述极点、极平面、极线这几个量之间的对应关系。

---

二、基础矩阵 F

1.基础矩阵原理

为了描述对极几何，引入基础矩阵F。对于一幅图像上的点x（图上p₁），在另一幅图像上存在对极线l’，并且在第二幅图像上，与x匹配的点x’（点p₂）必然在l’上。为了表示x与l’关系，我们令基础矩阵F定义为： l′=Fx。

假设第一幅图到第二幅图之间存在单应性变换H，则 x′=Hx。

又因为l’是表示过对极点e₂和图像点x’的直线，可以表示为： l′=e₂×x′=[e₂]xx′=[e₂]xHx。

所以可得 F=[e₂]xH。

其中e′=[a1,a2,a3]Te′=[a1,a2,a3]T，则它的反对称阵定义为：

在已知两个摄像机的射影矩阵P和P’时，对于图像上的一点x，可以得到其反投影射线方程为： X(λ)=P⁺ x+λC

其中P⁺ 是P的伪逆，即PP⁺ = I，C为摄像机中心。射线上的两点：P⁺ x（当λ=0）、C（当λ=∞）在第二个摄像机P’拍摄下，在第二幅视图上的点分别为P′P⁺ 和P′C，这两点过对极线l’，即 l′=(P′C)×(P′P⁺ x)=[e′]_x(P′P⁺ )x

可以推得 F=[e′]_xP′P⁺

2.基础矩阵性质

（1） 基础矩阵是秩为2、自由度为7的齐次矩阵。
（2）若x与x’是两幅图上的对应点，那么x′^TFx=0。
（3）l’是对应于x的对极线，l′=Fx。
（4）若e是第二个摄像机光心在第一幅图像上的极点，那么Fe=0 。

3.基础矩阵估算方法

3.1 八点估算法

基本矩阵是由该方程定义的： x′^TFx=0

其中x↔x′是两幅图像的任意一对匹配点。由于每一组点的匹配提供了计算F系数的一个线性方程，当给定至少7个点（3×3的齐次矩阵减去一个尺度，以及一个秩为2的约束），方程就可以计算出未知的F。我们记点的坐标为x=(x,y,1)^T，x′=(x′,y′,1)^T

又因为F为：

所以可得到方程：

即相应方程式为

给定n组点的集合，我们有如下方程：

如果存在确定（非零）解，则系数矩阵A的秩最多是8。由于F是齐次矩阵，所以如果矩阵A的秩为8，则在差一个尺度因子的情况下解是唯一的。可以直接用线性算法解得。

如果由于点坐标存在噪声则矩阵AA的秩可能大于8（也就是等于9，由于A是n×9的矩阵）。这时候就需要求最小二乘解，这里就可以用SVD来求解，f的解就是系数矩阵A最小奇异值对应的奇异向量，也就是A奇异值分解后A=UDV^T中矩阵V的最后一列矢量，这是在解矢量f在约束∥f∥下取∥Af∥最小的解。以上算法是解基本矩阵的基本方法，称为8点算法。

上述求解后的F不一定能满足秩为2的约束，因此还要在F的基础上加以约束。通过SVD分解可以解决，令F=UΣV^T，则

因为要秩为2，所以取最后一个元素设置为0，则

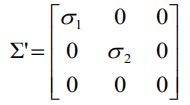
最终的解

3.2 RANSAC随机取样一致法估算（略）

---

三、基础矩阵代码实现

1.相关代码

from PIL import Image
from numpy import *
from pylab import *
from PCV.geometry import camera
from PCV.geometry import homography
from PCV.geometry import sfm
from PCV.localdescriptors import sift
from PCV.tools import ransac
import numpy as np


# Read features
im1 = array(Image.open('pic1.jpg'))
sift.process_image('imim1.jpg', 'img1.sift')

im2 = array(Image.open('pic2.jpg'))
sift.process_image('imim2.jpg', 'img2.sift')


l1, d1 = sift.read_features_from_file('img1.sift')
l2, d2 = sift.read_features_from_file('img2.sift')


matches = sift.match_twosided(d1, d2)

ndx = matches.nonzero()[0]
x1 = homography.make_homog(l1[ndx, :2].T)
ndx2 = [int(matches[i]) for i in ndx]
x2 = homography.make_homog(l2[ndx2, :2].T)

d1n = d1[ndx]
d2n = d2[ndx2]
x1n = x1.copy()
x2n = x2.copy()


#figure(figsize=(16,16))
sift.plot_matches(im1, im2, l1, l2, matches, True)
show()



#def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):
def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6):

    data = np.vstack((x1, x2))
    d = 10 # 20 is the original
    # compute F and return with inlier index
    F, ransac_data = ransac.ransac(data.T, model,
                                   8, maxiter, match_threshold, d, return_all=True)
    return F, ransac_data['inliers']

# find F through RANSAC
model = sfm.RansacModel()
F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-5)
print (F)


P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]])
P2 = sfm.compute_P_from_fundamental(F)


X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2)
# plot the projection of X
cam1 = camera.Camera(P1)
cam2 = camera.Camera(P2)
x1p = cam1.project(X)
x2p = cam2.project(X)

# figure(figsize=(16, 16))
imj = sift.appendimages(im1, im2)
imj = vstack((imj, imj))

imshow(imj)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1p[0])):
    if (0<= x1p[0][i]<cols1) and (0<= x2p[0][i]<cols1) and (0<=x1p[1][i]<rows1) and (0<=x2p[1][i]<rows1):
        plot([x1p[0][i], x2p[0][i]+cols1],[x1p[1][i], x2p[1][i]],'c')
axis('off')
show()

d1p = d1n[inliers]
d2p = d2n[inliers]

# Read features
im3 = array(Image.open('pic2.jpg'))
sift.process_image('pic2.jpg', '3.sift')
l3, d3 = sift.read_features_from_file('3.sift')

matches13 = sift.match_twosided(d1p, d3)

ndx_13 = matches13.nonzero()[0]
x1_13 = homography.make_homog(x1p[:, ndx_13])
ndx2_13 = [int(matches13[i]) for i in ndx_13]
x3_13 = homography.make_homog(l3[ndx2_13, :2].T)

#figure(figsize=(16, 16))
imj = sift.appendimages(im1, im3)
imj = vstack((imj, imj))

imshow(imj)

cols1 = im1.shape[1]
rows1 = im1.shape[0]
for i in range(len(x1_13[0])):
    if (0<= x1_13[0][i]<cols1) and (0<= x3_13[0][i]<cols1) and (0<=x1_13[1][i]<rows1) and (0<=x3_13[1][i]<rows1):
        plot([x1_13[0][i], x3_13[0][i]+cols1],[x1_13[1][i], x3_13[1][i]],'c')
axis('off')
show()

P3 = sfm.compute_P(x3_13, X[:, ndx_13])

print ('P1',P1)
print ('P1',P2)
print ('P1',P3)

2.实验结果

2.1 室外场景（距离相近）

前两张图sift特征匹配图：

经过ransac算法筛选后的特征点匹配图：

第一张图与另一张图经过ransac算法筛选后的特征匹配图：

得到的基础矩阵F:

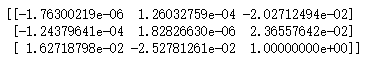
得到空间三维点P1,P2,P3分别为：

2.2 室外场景（距离不同）

sift特征匹配图：

经过ransac算法筛选后的特征点匹配图：

与第三张图经过ransac算法筛选后的特征点匹配：

得到的基础矩阵F:

三维点分别为：

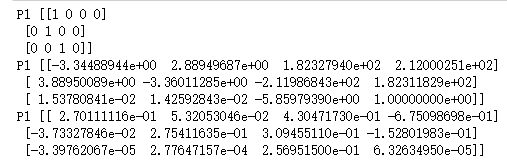
2.3 室内场景

sift特征匹配图：

经过ransac算法筛选后的特征点匹配图：

与第三张图经过ransac算法筛选后的特征点匹配图：

得到的基础矩阵F：

三维点：

---

四、实验总结

从实验结果可以看出，图像的特征匹配的准确度室外距离相近的图像会高于室外距离不同的图像和室内的图像。

在实验中会遇到问题：

这是因为图像sift特征匹配的匹配点数过少，这时候需要修改代码中匹配的阈值。但是，sift特征匹配的匹配对过少的话，会对后续进行ransac算法实现产生影响，所以拍摄图片的时候要特别注意。