数据预处理Part7——特征选择
文章目录
- 特征选择:
- 1. 什么是特征选择?
- 2. 为什么要进行特征选择?
- 3. 怎样进行特征选择
- 3.1 Filter过滤法
- 3.1.1 方差过滤
- a. VarianceThreshold
- b. 方差过滤对模型的影响:
- 3.1.2 相关性过滤
- 3.1.2.1 卡方过滤
- a 卡方过滤
- b. 选取超参数K
- 3.1.2.2 F检验
- 3.1.2.3 互信息法
- 3.1.3 总结
- 3.2 Embedded嵌入法
- 3.3 Wrapper包装法
- 4. 总结
特征选择:
1. 什么是特征选择?
特征选择就是从所有的特征中,选择出有意义,对模型有帮助的特征,以避免必须将所有特征都导入模型去训练的情况。
特征选择完全独立于任何机器学习算法。他是根据各种统计检验中的分数以及相关性的各项指标来选择特征。
2. 为什么要进行特征选择?
在实际工作中,用于模型中的特征维度往往很高,维度过高会增大模型计算复杂度,而且在这么多维数据中,并不是每个特征对模型的预测都是有效果的,所以需要利用一些方法去除一些不必要特征,从而降低模型的计算复杂度。
3. 怎样进行特征选择
常见的特征选择方法:
- 过滤法
- 嵌入法
- 包装法
- 降维算法
3.1 Filter过滤法
3.1.1 方差过滤
a. VarianceThreshold
Variance:方差。Threshold:阈。这是通过特征本身的方差来筛选特征的类,比如一个特征本身的方差很小,就表示样本在这个特征上基本没有差异,可能特征中的大多数值都一样,甚至整个特征的取值都相同,那这个特征对于样本区分没有什么作用。所以无论接下来的特征工程要做什么,都要优先消除方差为0的特征。
VarianceThreshold中有重要参数threshold,也就是方差的阈值,表示舍弃所有方差小于threshold的特征,不填默认为0,即删除所有的记录都相同的特征。
引包:
import pandas as pd
import numpy as np
from sklearn.feature_selection import VarianceThreshold
数据加载:
data = pd.read_csv("digit recognizor.csv")
data.head()
data.shape
(42000, 785)
缺失值处理:
data.fillna(0,inplace = True)
切分特征和标签:
x,y = data.iloc[:,1:],data.iloc[:,0]
以0为阈值进行方差过滤:
model_var = VarianceThreshold()
x_var0 = model_var.fit_transform(x)
x_var0.shape
(42000, 708)
以方差中位数为阈值进行方差过滤:
medium_var = np.median(x.var())
model_var = VarianceThreshold(threshold=medium_var)
x_var_medium = model_var.fit_transform(x)
x_var_medium.shape
(42000, 392)
b. 方差过滤对模型的影响:
我们这样做了以后,对模型效果会有怎样的影响呢?我们通过对比KNN和随机森林分别在方差过滤前和方差过滤后运行的效果和运行时间来说明。KNN是K近邻算法中的分类算法,其原理非常简单,是利用每个样本到其他样本点的距离来判断每个样本点的相似度,然后对样本进行分类。KNN必须遍历每个特征和每个样本,因而特征越多,KNN的计算也就会越缓慢。
这一部分代码运算时间很长,这里我使用colab环境进行运行。
KNN算法方差过滤前:
from sklearn.neighbors import KNeighborsClassifier as KNN
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
```python
cross_val_score(KNN(),x,y,cv=5).mean()
0.9658569700264943
%%timeit
cross_val_score(KNN(),x,y,cv=5).mean()
KNN算法方差过滤后:
cross_val_score(KNN(),x_fsvar,y,cv=5).mean()
0.9659997478150573
%%timeit
cross_val_score(KNN(),x_fsvar,y,cv=5).mean()

对于KNN,过滤后的效果十分明显:准确率稍有提升,耗费时间减少了近一半。
随机森林算法方差过滤前:
cross_val_score(RFC(random_state=0),x,y,cv=5).mean()
0.9380003861799541
%%timeit
cross_val_score(RFC(n_estimators=10,random_state=0),x,y,cv=5).mean()
19.4 s ± 1.26 s per loop (mean ± std. dev. of 7 runs, 1 loop each)
随机森林算法方差过滤后:
cross_val_score(RFC(random_state=0),x_var_medium,y,cv=5).mean()
0.9388098166696807
cross_val_score(RFC(random_state=0),x_var_medium,y,cv=5).mean()
19.1 s ± 1.38 s per loop (mean ± std. dev. of 7 runs, 1 loop each)
首先可以观察到的是,随机森林的准确率略逊于KNN,但运行时间却连KNN的1%都不到,只需要十几秒钟。其次,方差过滤后,随机森林的准确率也微弱上升,但运行时间却几乎是没什么变化,依然是19秒钟。
为什么随机森林运行如此之快?为什么方差过滤对随机森林没很大的有影响?这是由于两种算法的原理中涉及到的计算量不同。最近邻算法KNN,单棵决策树,支持向量机SVM,神经网络,回归算法,都需要遍历特征或升维来进行运算,所以他们本身的运算量就很大,需要的时间就很长,因此方差过滤这样的特征选择对他们来说就尤为重要。
但对于不需要遍历特征的算法,比如随机森林,它随机选取特征进行分枝,本身运算就非常快速,因此特征选择对它来说效果平平。这其实很容易理解,无论过滤法如何降低特征的数量,随机森林也只会选取固定数量的特征来建模;而最近邻算法就不同了,特征越少,距离计算的维度就越少,模型明显会随着特征的减少变得轻量。因此,过滤法的主要对象是:需要遍历特征或升维的算法们,而过滤法的主要目的是:在维持算法表现的前提下,帮助算法们降低计算成本
3.1.2 相关性过滤
方差挑选之后,我们就要考虑下一个问题:相关性。我们希望选出与标签相关且有意义的特征,因为这样的特征能够为我们提供大量信息、如果特征与标签无关,那只会白白浪费时间,可能还会给模型带来噪音。在sklearn当中,我们有三种常用的方法评判特征与标签之间的相关性:卡方检验,F检验,互信息
3.1.2.1 卡方过滤
a 卡方过滤
卡方过滤是专门针对离散型标签(分类)的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量,并按照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest这个可以输入“评分标准”来选出前K个分数最高的特征的类,我们可以借此除去最可能独立于标签,与我们分类目的无关的特征。
另外,如果卡方检验检测到某个特征中的所有值都相同,会提示我们使用方差先进行方差过滤,并且我们已经验证过,当我们使用方差过滤筛选掉一半的特征后,模型的表现是提升的。因此在这里,我们使用threshold=中位数完成的方差过滤的数据来做卡方检验:
引包:
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
卡方过滤:
model_chi2 = SelectKBest(chi2,k=300)
x_chi2 = model_chi2.fit_transform(x_var_medium,y)
x_chi2.shape
(42000, 300)
模型效果对比:
cross_val_score(RFC(random_state=0),x_var_medium,y,cv=10).mean()
0.9411198132299345
cross_val_score(RFC(random_state=0),x_chi2,y,cv=10).mean()
0.9378586603630324
可以看出,模型的效果降低了,这说明我们在设定k=300的时候删除了与模型相关且有效的特征,我们的K值设置得太小,要么我们需要调整K值,要么我们必须放弃相关性过滤。当然,如果模型的表现提升,则说明我们的相关性过滤是有效地,是过滤掉了模型的噪音的,这时候我们就保留相关性过滤的结果。
b. 选取超参数K
那如何设置一个最佳的K值呢?在现实数据中,数据量很大,模型很复杂的时候,我们也许不能先去跑一边模型看看效果,而是希望最开始就能选择一个最优的超参数K,那第一个方法就是我们之前提到过的学习曲线:
score_list = []
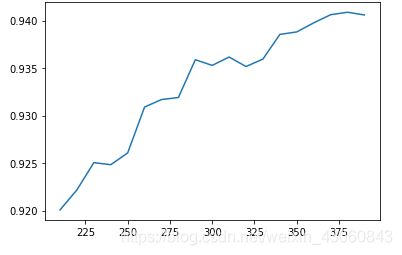
for i in range(390,200,-10):
x_chi2 = SelectKBest(chi2,k=i).fit_transform(x,y)
score = cross_val_score(RFC(random_state=0),x_chi2,y,cv=10).mean()
score_list.append(score)
plt.plot(range(390,200,-10),score_list)
plt.show()
通过这条曲线,我们可以观察到,随着K值得不断增加,模型的表现不断上升。这说明,K越大越好,数据中所有的特征都是与标签相关的。但是运行这条曲线的时间同样也是非常长,接下来我们就来介绍一种更好的选择K的方法:看P值选择K
卡方检验的本质是推测两种数据之间的差异,其检验的原假设是 “两组数据是相互独立的”。卡方检验返回卡方值和P值两个统计量,其中卡方值很难界定有效的范围,而P值,我们一般使用0.01或0.05作为显著性水平,即P值判断的边界,具体我们可以这样来看:
| P值 | <=0.05或0.01 | >0.05或0.01 |
|---|---|---|
| 数据差异 | 差异不是自然形成的 | 这些差异是很自然的样本误差 |
| 相关性 | 两组数据是相关的 | 亮度数据是相互独立的 |
| 原假设 | 拒绝原假设,接受备选假设 | 接受原假设 |
从特征工程的角度,我们希望选取卡方值很大,P值小于0.05的特征,即和标签是相关联的特征。而调用SelectKBest之前,我们可以直接从chi2实例化的模型中获得各个特征所对应的卡方值和P值。
chivalue,pvalue = chi2(x_var_medium,y) # 计算卡方值和P值
chivalue[:10] # 计算得出前10个卡方值
array([ 945664.84392643, 1244766.05139164, 1554872.30384525,
1834161.78305343, 1903618.94085294, 1845226.62427198,
1602117.23307537, 708535.17489837, 974050.20513718,
1188092.19961931])
pvalue[:10] # 计算得出前10个P值
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
k = x_var_medium.shape[1] - (pvalue>0.05).sum() # 计算选取特征数
k
通过观察,所有的特征P值都是0,这说明对于dight_recignizor这个数据集来说,方差验证已经把所有和标签无关的特征都剔除了,或者这个数据集本身就不含与标签无关的特征。在这种情况下,舍弃任何一个特征,都会舍弃对模型有用的信息,而是模型表现下降,因此我们对计算速度感到满意时,我们不需要使用相关性过滤来过滤我们的数据,我们试试用其他的相关性过滤方法验证一下我们在这个数据集上的结论。
3.1.2.2 F检验
F检验,又称ANOVA,方差齐性检验,是用来捕捉每个特征与标签之间的线性关系的过滤方法。它既可以做回归也可以做分类,因此包含feature_selection.f_classif和feature_selection.regression两个类。其中F检验分类用于标签是离散型变量的数据,而F检验回归用于标签是连续性变量的数据。
和卡方检验一样,这两个类需要和类SelectKBest连用,并且我们也可以直接通过输出的统计量来判断我们到底要设置一个什么样的K。需要注意的是,F检验在数据服从正态分布时效果会非常稳定,因此如果使用F检验过滤,我们会先将数据转换成服从正态分布的形式。
F检验的本质是寻找两组数据之间的线性关系,其原假设是数据不存在显著的线性关系。它返回F值和P值两个统计量。和卡方过滤一样,我们希望选取P值小于0.05或0.01的特征,这些特征与标签是显著线性相关的,而P值大于0.05或0.01的特征则被我们认为是和标签没有显著线性关系的特征,应该被删除。以F检验的分类为例,我们继续在数字数据集上来进行特征选择:
引包:
from sklearn.feature_selection import f_classif
F检验计算P值:
F,pvalues_f = f_classif(x_var_medium,y)
pvalues_f[:10]
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
计算特征选取个数:
k = F.shape[0] - (pvalues_f > 0.05).sum()
k
392
得到的结论和我们用卡方过滤得到的结论一模一样:没有任何特征的P值大于0.01.所有的特征都是和标签相关的,因此我们不需要相关性过滤。
3.1.2.3 互信息法
互信息法是用来捕捉每个特征与标签之间的任意关系(包括线性和非线性关系)的过滤方法。和F检验相似,它既可以做回归也可以做分类,并且包含两个类feature_selection.mutual_info_classif和feature_selection.mutual_info_regression.这两个类的用法和参数都和F检验一模一样,不过互信息法比F检验更加强大,F检验只能够找出线性关系,而互信息法可以找出任意关系。
互信息法不返回P值和F值类似的统计量,他返回每个特征与目标之间打的互信息量的估计,这个估计量在[0.1]之间取值,为0则表示两个变量独立,为1则表示两个变量完全相关。以互信息分类为例的代码如下:
引包:
from sklearn.feature_selection import mutual_info_classif as MIC
result = MIC(x_var_medium,y)
result[:10]
array([0.06271997, 0.08577215, 0.10750456, 0.11162415, 0.11419952,
0.10023697, 0.08377809, 0.05608807, 0.0715175 , 0.10122818])
计算特征选取个数:
k = result.shape[0] - sum(result<=0)
k
392
所有特征的互信息量估计都大于0,因此所有特征都与标签相关。
无论是F检验还是互信息法,都可以使用学习曲线,只是使用统计量的方法会更加高效。当统计量判断已经没有特征可以删除时,无论用学习曲线如何跑,删除特征都只会降低模型的表现。当然了,如果数据量太庞大,模型太复杂,我们还是可以牺牲模型表现来提升模型速度,一切都看大家的具体需求。
3.1.3 总结
| 类 | 说明 | 超参数的选择 |
|---|---|---|
| VarianceThreshold | 方差过滤,可输入方差阈值,返回方差大于阈值的新特征矩阵 | 看具体数据究竟是含有更多噪声还是更多有效特征。一般就使用0或1筛选,也可以画学习曲线或者取中位数跑模型来帮忙确认 |
| SelectKBest | 用来选取K个统计量结果最佳的特征,生成符合统计量要求的新特征矩阵 | 看配合使用的统计量 |
| chi2 | 卡方检验,专用于分类算法,捕捉相关性 | 选择P小于显著性水平的特征 |
| f_classif | F检验分类,只能捕捉线性相关性,要求数据服从正态分布 | 追求P小于显著性水平的特征 |
| f_regression | F检验回归,只能捕捉线性相关性,要求数据服从正态分布 | 追求P小于显著性水平的特征 |
| mutual_info_classif | 互信息分类,可以捕捉任何相关性,不能用于稀疏矩阵 | 追求互信息估计大于0的特征 |
| mutual_info_regression | 互信息回归,可以捕捉任何相关性,不能用于稀疏矩阵 | 追求互信息估计大于0的特征 |
3.2 Embedded嵌入法
嵌入法是一种让算法自己决定使用哪些特征的方法,即特征选择和算法训练同时进行。在使用嵌入法时,我们先试用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据权值系数从大到小选择特征。这些权值系数往往代表了特征对于模型的某种贡献或某种重要性,比如决策树和随机森林中的feature_importances_属性,可以列出各个特征对树的建立的贡献,我们就可以基于这种贡献的评估,找出对模型建立最有用的特征。因此相比于过滤法,嵌入法的结果会更加精确到模型的效用本身,对于提高模型效力有更好的结果。并且,由于考虑特征对模型的贡献,因此无关的特征(需要相关性过滤的特征)和无区分度的特征(需要方差过滤的特征)都会因为缺乏对模型的贡献而被删除掉,可谓是过滤法的进化版。
然而,嵌入法也不是没有缺点。过滤法中使用的统计量可以使用统计知识和常识来查找范围(如P值)。而嵌入法中使用的权值系数却没有这样的范围可找,我们可以说,权值系数为0的特征对模型丝毫没有作用。但当大量特征都对模型有贡献且贡献不一时,我们就很难去界定一个有效的临界值。这种情况下,模型权值系数就是我们的超参数,我们或许需要学习曲线,或者根据模型本身的某些性质去判断这个超参数的最佳值究竟应该是多少。
3.3 Wrapper包装法
包装法也是一个特征选择和算法训练同时进行的方法,与嵌入法十分相似,他也是依赖于算法自身的选择,比如coef_属性或feature_importances_属性来完成特征选择。但不同的是,我们往往使用一个目标函数作为黑盒来帮助我们选取特征,而不是自己输入某个评估指标或统计量的阈值。包装法在初始特征集上训练评估器,并且通过coef_属性或通过feature_importances_属性获得每个特征的重要性。然后,从当前的一组特征中修剪最不重要的特征。在修剪的集合上递归地重复该过程,直到最终到大所需数量的要选择的特征。区别于过滤法和嵌入法的一次训练解决所有问题,包装法要使用特征子集进行多次训练,因此他所需要的计算成本是最高的。
注意,这个算法指的不是我们最终用来导入数据的分类或回归算法,而是专业的数据挖掘算法,即我们的目标函数。这些数据挖掘算法的核心功能就是选取最佳特征子集。
最典型的目标函数是递归特征消除法。他是一种贪婪的优化算法,旨在找到性能最佳的特征子集。它反复创建模型,并在每次迭代时保留最佳特征或剔除最差特征,下一次迭代时,他会使用上一次建模中没有被选中的特征来构建下一个模型,直到所有特征都耗尽为止。然后,他根据自己保留或剔除特征的顺序来对特征进行排名,最终选出一个最佳子集。包装法的效果是所有特征选择方法中最利于提升模型表现的,他可以使用很少的特征达到很优秀的效果。除此之外,在特征数目相同时,包装法和嵌入法的效果能够匹敌,不过它比嵌入法算的更加缓慢,所以也不适用于太大型的数据。相比之下,包装法是最能保证模型效果的特征选择方法。
代码实现:
引包:
from sklearn.feature_selection import RFE
n_features_to_select:想要特征的个数;
step:每次迭代中希望溢出的特征个数
selector = RFE(RFC(random_state=0),n_features_to_select=340,step=50).fit(x,y)
selector.support_.sum() # support_返回所有特征最后是否被选中的布尔矩阵
selector.ranking_ # 返回特征按迭代次数中重要性排名
X_wrapper = selector.transform(x)
cross_val_score(RFC(random_state=0),X_wrapper,y,cv=10).mean()
0.9412862149257508
4. 总结
经验来说,过滤法更快速,但更粗糙。包装法和嵌入法更精确,比较适合具体到算法去调整,但计算量比较大,运行时间长。当数据量很大的时候,优先使用方差过滤和互信息法调整,在上其他特征选择方法。使用逻辑回归时,优先使用嵌入法。使用支持向量机时,优先使用包装法。
参考资料:《菜菜的sklearn学习》
关联文章:
数据预处理Part1——数据清洗
数据预处理Part2——数据标准化
数据预处理Part3——真值转换
数据预处理Part4——数据离散化
数据预处理Part5——样本分布不均衡
数据预处理Part6——数据抽样
数据预处理Part8——数据共线性
数据预处理Part9——数据降维