数据预处理Part8——数据共线性
文章目录
- 1. 什么是数据共线性
- 2. 为什么会出现数据共线性
- 3. 如何检验共线性?
- 4. 如何解决数据共线性?
- 5. 代码实现
1. 什么是数据共线性
所谓共线性问题是指输入的自变量之间存在较高的线性相关度。共线性问题会导致回归模型的稳定性和准确性大大降低,另外,过多无关的维度参与计算也会浪费计算资源和时间。
常见的具有明显的共线性的维度或变量如下:
- 访问量和页面浏览量
- 页面浏览量和访问时间
- 订单量和销售额
- 订单量和转化率
- 促销费用和销售额
- 网络展示广告费用和访客数
2. 为什么会出现数据共线性
导致出现变量间共线性的原因可能包括:
-
数据样本不够,导致共线性存在偶然性,这其实反映了缺少数据对于数据建模的影响,共线性仅仅是影响的一部分
-
多个变量都基于时间,有共同或相反的演变趋势,例如,春节期间的网络销售量和销售额都相对正常时间有下降趋势
-
多个变量间存在一定的推移关系,但总体上变量间的趋势一致,只是发生的时间点不一致,例如品牌广告费用和销售额之间,通常是品牌广告先进行大范围的曝光和信息推送,经过一定时间传播之后,销售额才能爆发出来。
-
多个变量间存在近似线性的关系。例如,用y代表访客数,用x代表展示广告费用,那么二者的关系很可能是y = 2x+b,即每投放1元钱,可以带来大概2-3个访客。
3. 如何检验共线性?
共线性一般通过容忍度、方差膨胀因子、特征值这几个特征数据来检验。
-
容忍度:容忍度是每个自变量作为因变量对其他自变量进行回归建模时得到的残差比例,大小用1减得到的决定系数来表示。容忍度的值介于0和1之间,值越小,说明这个自变量与其他自变量间存在共线性问题的可能性越大。
-
方差膨胀因子:VIF时容忍度的倒数,值越大则共线性问题越明显,通常以10作为判断边界。VIF<10,不存在多重共线性;10<=VIF<=100,存在较强的多重共线性;VIF>100,存在严重多重共线性。
-
特征值:该方法实际上就是对自变量进行主成分分析,如果多个维度的特征值等于0,则可能存在严重的共线性。
4. 如何解决数据共线性?
解决共线性的5种常用方法:
-
增大样本量
通过增加样本量来消除由于数据量不足而出现的偶然共线性现象。在可行的前提下这种方法是需要优先考虑的。但即使增加了样本量,可能也无法解决共线性问题,原因是很可能变量间确实群在这个问题。 -
岭回归法
岭回归分析是一种专用于共线问题的有偏估计回归方法,实质上一种改良的最小二乘估计法。它通过放弃最小二乘法的无偏性。以损失部分信息、降低精度为代价来获得更实际和可能性更强的回归系数。因此岭回归在存在较强共线性的回归应用中较为常用。 -
逐步回归法
逐步回归法是每次引入一个自变量并进行统计检验,然后逐步引用其他变量,同时对所有变量的回归系数进行检验。如果原来引入的变量由于后面变量的引入而变得不再显著,那么就将其剔除,逐步得到最优回归方程 -
主成分回归
通过主成分分析,将原始参与建模的变量 转换为少数几个主成分,每个主成分是原变量的线性组合,然后基于主成分做回归分析,这样也可以在不丢失重要数据特征的前提下避开共线性问题 -
人工去除
直接结合人工经验,对参与回归模型计算的自变量进行删减,也是一个较为常用的方法。但是这种方法需要操作者对于业务、模型和数据都有相对深入的理解,才有可能作出正确的操作。从专业角度分析,如果缺少上述三个方面中的任何一个,那么人工去除的方式都可能上升偏差,导致结果不准确。
5. 代码实现
引包:
import pandas as pd
import numpy as np
from sklearn.linear_model import Ridge # 岭回归
from sklearn.decomposition import PCA # 主成分分析
from sklearn.linear_model import LinearRegression # 普通线性回归
加载数据:
data = np.loadtxt('data5.txt')
data
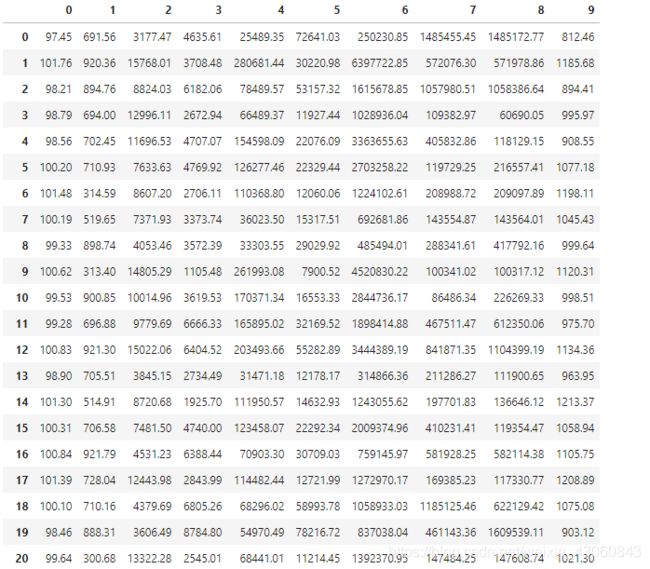
pd.DataFrame(data)
x,y = data[:,:-1],data[:,-1]
使用岭回归算法进行回归分析:
model_ridge = Ridge(alpha=0.1)
model_ridge = model_ridge.fit(x,y)
model_ridge.coef_
array([ 8.51015136e+01, -1.17978960e-03, 9.75430688e-04, -8.54480234e-04,
2.10126097e-05, 2.20628066e-04, -3.01072765e-06, -9.30743470e-06,
-3.72997438e-08])
model_ridge.intercept_
-7452.444035259182
使用主成分回归进行回归分析:
model_pca = PCA()
data_pca = model_pca.fit_transform(x)
ratio_cumsm = np.cumsum(model_pca.explained_variance_ratio_)
ratio_cumsm
array([0.9028 , 0.98570494, 0.99957412, 0.99995908, 0.99999562,
0.99999939, 0.99999999, 1. , 1. ])
rule_index = np.where(ratio_cumsm>0.8)
rule_index
(array([0, 1, 2, 3, 4, 5, 6, 7, 8], dtype=int64),)
min_index = rule_index[0][0]
min_index
0
data_pca_result = data_pca[:,:min_index+1]
len(data_pca_result)
1000
model_linear = LinearRegression()
model_linear.fit(data_pca_result,y)
model_linear.coef_
[1.26262171e-05]
model_linear.model_linear.intercept_
1058.52726
参考资料:《Python数据分析与数据化运营》
关联文章:
数据预处理Part1——数据清洗
数据预处理Part2——数据标准化
数据预处理Part3——真值转换
数据预处理Part4——数据离散化
数据预处理Part5——样本分布不均衡
数据预处理Part6——数据抽样
数据预处理Part7——特征选择
数据预处理Part9——数据降维