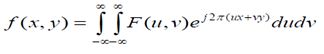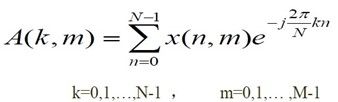数字图像处理学习笔记 四 傅里叶变换和频率域滤波

目录

 

一 预备知识：傅里叶级数的介绍

1、一维傅里叶变换数学推导

2、图像傅里叶变换的物理意义

3、二维傅里叶变换

 

二、频率域滤波

1、频率域与空间域之间的关系

2、频率域滤波的基本步骤

3、使用频率域滤波平滑图像

4、使用频率域滤波锐化图像

5、选择率滤波器

6、同态滤波

---

一 预备知识：傅里叶级数的介绍

1、一维傅里叶变换数学推导

傅里叶级数，形如：

是由三角函数系

              1，cosx，sinx，cos2x，sin2x，…，cosnx，sinnx，…(2)

经过组合所产生的三角级数。a0，an，bn 称为傅里叶系数。为了求傅里叶系数，我们先引出下面的预备知识：

三角函数系(2)中任何两个不相同的函数的乘积在 [−T2，T2]上的积分等于0。即：

而三角函数系(2)中任何两个相同函数的乘积在 [−T2，T2] 上的积分都不等于0。

 对（1）式在 [−T2，T2] 逐项积分，

上式右边括号内的积分等于0，所以

转化一下：

现以 cos(nωx)乘（1）式两端，再同上逐项积分，我们得到：

由于等式右边除了 

                            

外，其他积分项都等于0，化简后有：

                           

同理，用 sin(nωx) 乘以（1）两端并在 [−T2，T2] 逐项积分，可得

这时用欧拉公式化简系数成指数形式：

进一步得到：

将上式代入（3）式，我们得到傅里叶变换的指数公式：

推荐！b站up主对傅里叶级数进行了生动易懂的教学~，可以跟着算一遍，加深理解！
纯干货数学推导_傅里叶级数与傅里叶变换_Part1_三角函数的正交性 （一共有6个视频）

2、图像傅里叶变换的物理意义

       图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。傅里叶变换在实际中有非常明显的物理意义，设f是一个能量有限的模拟信号，则其傅里叶变换就表示f的频谱。从纯粹的数学意义上看，傅里叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看，傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域。换句话说，傅里叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数。

       傅里叶逆变换是将图像的频率分布函数变换为灰度分布函数傅里叶变换以前，图像（未压缩的位图）是由对在连续空间（现实空间）上的采样得到一系列点的集合，通常用一个二维矩阵表示空间上各点，记为z=f(x,y)。又因空间是三维的，图像是二维的，因此空间中物体在另一个维度上的关系就必须由梯度来表示，这样我们才能通过观察图像得知物体在三维空间中的对应关系。

       傅里叶频谱图上我们看到的明暗不一的亮点，其意义是指图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小（可以这么理解，图像中的低频部分指低梯度的点，高频部分相反）。一般来讲，梯度大则该点的亮度强，否则该点亮度弱。这样通过观察傅里叶变换后的频谱图，也叫功率图，我们就可以直观地看出图像的能量分布：如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小）；反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的、边界分明且边界两边像素差异较大的。

       对频谱移频到原点以后，可以看出图像的频率分布是以原点为圆心，对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外，还有一个好处，它可以分离出有周期性规律的干扰信号，比如正弦干扰。一幅频谱图如果带有正弦干扰，移频到原点上就可以看出，除了中心以外还存在以另一点为中心、对称分布的亮点集合，这个集合就是干扰噪音产生的。这时可以很直观的通过在该位置放置带阻滤波器消除干扰。

3、二维傅里叶变换

        二维离散傅里叶变换：(Two-Dimensional Discrete Fourier Transform)是一种数字变换方法，一般应用于将图像从空间域转至频域，在图像增强、图像去噪、图像边缘检测、图像特征提取、图像压缩等等应用中都起着极其重要的作用。

• 频谱：对一个时域信号进行傅里叶变换，就可以得到的信号的频谱，信号的频谱由两部分构成：幅度谱和相位谱，相位谱描述各    个分量的相位随角频率的变化。幅度谱描述各个分量的幅度随着频率的变化。
• 功率谱：为信号频谱的平方。可观察图像的能量分布，如果频谱图中暗的点数更多，那么实际图像是比较柔和的（因为各点与邻域差异都不大，梯度相对较小），反之，如果频谱图中亮的点数多，那么实际图像一定是尖锐的，边界分明且边界两边像素差异较大的。
• 相位：表示相对于原始波形，这个波形的偏移量（左或右）。
• 频域：频域就是频率域，平常我们用的是时域，是和时间有关的，这里只和频率有关，是时间域的倒数。时域中，X轴是时间，频域中是频率。频域分析就是分析它的频率特性。

 3.1二维傅里叶变换

     二维Fourier变换:

    逆变换：

3.2二维离散傅里叶变换

       一个图像尺寸为M×N的 函数的离散傅里叶变换由以下等式给出：

      其中变量u和v用于确定它们的频率，频域系统是由所张成的坐标系，其中和用做（频率）变量。空间域是由f(x,y)所张成的坐标系。可以得到频谱系统在频谱图四角处沿和方向的频谱分量均为0。

      离散傅里叶逆变换由下式给出：

     令R和I分别表示F的实部和需部，则傅里叶频谱，相位角，功率谱（幅度）定义如下：

3.3用FFT计算二维离散傅里叶变换

      二维离散傅里叶变换的定义为：

   二维离散傅里叶变换可通过两次一维离散傅里叶变换来实现:

（1）作一维N点DFT（对每个m做一次，共M次）

（2）作M点的DFT（对每个k做一次，共N次）

这两次离散傅里叶变换都可以用快速算法求得,若M和N都是2的幂,则可使用基二FFT算法,所需要乘法次数为                                  

而直接计算二维离散傅里叶变换所需的乘法次数为（M+N）MN，当M和N比较大时用用FFT运算，可节约很多运算量

3.4二维离散傅里叶变换的性质

(1）分离性

       二维离散傅里叶变换具有分离性

       分离性质的主要优点是可借助一系列一维傅里叶变换分两步求得。第1步，沿着的每一行取变换，将其结果乘以1/N,取得二维函数;第2步，沿着的每一列取变换，再将结果乘以1/N,就得到了。这种方法是先行后列。如果采用先列后行的顺序，其结果相同。

       如图：

     对逆变换f(x,y)也可以类似地分两步进行。

(2）平移性

       傅里叶变换和逆变换对的位移性质是指：

 

由乘以指数项并取其乘积的傅立叶变换，使频率平面的原点位移至。同样地，以指数项乘以并取其反变换，将空间域平面的原点位移至当N/2时，指数项为：

即为

       这样，用(x+y)乘以就可以将的傅里叶变换原点移动到N*N频率方阵的中心，这样才能看到整个谱图。另外，对的平移不影响其傅里叶变换的幅值。

       此外，与连续二维傅里叶变换一样，二维离散傅里叶变换也具有周期性、共轭对称性、线性、旋转性、相关定理、卷积定理、比例性等性质。这些性质在分析及处理图像时有重要意义。

3.5二维离散傅里叶变换图像性质

     1、图像经过二维傅里叶变换后，其变换系数矩阵具有如下性质：若变换矩阵原点设在中心，其频谱能量集中分布在变换系数短阵的中心附近(图中阴影区)。若所用的二维傅里叶变换矩阵的原点设在左上角，那么图像信号能量将集中在系数矩阵的四个角上。这是由二维傅里叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。

     2、图像灰度变化缓慢的区域，对应它变换后的低频分量部分；图像灰度呈阶跃变化的区域，对应变换后的高频分量部分。除颗粒噪音外，图像细节的边缘、轮廓处都是灰度变化突变区域，它们都具有变换后的高频分量特征。

 实验：用python实现快速傅里叶变换与频率域滤波 ：

def triangle_wave(size, T):
    t = np.linspace(-1, 1, size, endpoint=False)
    # where
    # y = np.where(t < 0, -t, 0)
    # y = np.where(t >= 0, t, y)
    y = np.abs(t)
    y = np.tile(y, T) - 0.5
    x = np.linspace(0, 2*np.pi*T, size*T, endpoint=False)
    return x, y


def sawtooth_wave(size, T):
    t = np.linspace(-1, 1, size)
    y = np.tile(t, T)
    x = np.linspace(0, 2*np.pi*T, size*T, endpoint=False)
    return x, y


def triangle_wave2(size, T):
    x, y = sawtooth_wave(size, T)
    return x, np.abs(y)


def non_zero(f):
    f1 = np.real(f)
    f2 = np.imag(f)
    eps = 1e-4
    return f1[(f1 > eps) | (f1 < -eps)], f2[(f2 > eps) | (f2 < -eps)]


if __name__ == "__main__":
    mpl.rcParams['font.sans-serif'] = ['simHei']
    mpl.rcParams['axes.unicode_minus'] = False
    np.set_printoptions(suppress=True)

    x = np.linspace(0, 2*np.pi, 16, endpoint=False)
    print('时域采样值：', x)
    y = np.sin(2*x) + np.sin(3*x + np.pi/4) + np.sin(5*x)
    # y = np.sin(x)

    N = len(x)
    print('采样点个数：', N)
    print('\n原始信号：', y)
    f = np.fft.fft(y)
    print('\n频域信号：', f/N)
    a = np.abs(f/N)
    print('\n频率强度：', a)

    iy = np.fft.ifft(f)
    print('\n逆傅里叶变换恢复信号：', iy)
    print('\n虚部：', np.imag(iy))
    print('\n实部：', np.real(iy))
    print('\n恢复信号与原始信号是否相同：', np.allclose(np.real(iy), y))

    plt.figure(facecolor='w')
    plt.subplot(211)
    plt.plot(x, y, 'go-', lw=2, mec='k')
    plt.title('时域信号', fontsize=15)
    plt.grid(b=True, ls=':', color='#404040')
    plt.subplot(212)
    w = np.arange(N) * 2*np.pi / N
    print('频率采样值：', w)
    plt.stem(w, a, linefmt='r-', markerfmt='ro')
    plt.title('频域信号', fontsize=15)
    plt.grid(b=True, ls=':', color='#404040')
    plt.show()

    # 三角/锯齿波
    x, y = triangle_wave(20, 5)
    # x, y = sawtooth_wave(20, 5)
    N = len(y)
    f = np.fft.fft(y)
    # print '原始频域信号：', np.real(f), np.imag(f)
    print('原始频域信号：', non_zero(f))
    a = np.abs(f / N)

    # np.real_if_close
    f_real = np.real(f)
    eps = 0.3 * f_real.max()
    print('f_real = \n', f_real)
    print(eps)
    f_real[(f_real < eps) & (f_real > -eps)] = 0
    f_imag = np.imag(f)
    eps = 0.3 * f_imag.max()
    print(eps)
    f_imag[(f_imag < eps) & (f_imag > -eps)] = 0
    f1 = f_real + f_imag * 1j
    y1 = np.fft.ifft(f1)
    y1 = np.real(y1)
    # print '恢复频域信号：', np.real(f1), np.imag(f1)
    print('恢复频域信号：', non_zero(f1))

    plt.figure(figsize=(8, 8), facecolor='w')
    plt.subplot(311)
    plt.plot(x, y, 'g-', lw=2, mec='k')
    plt.title('三角波', fontsize=15)
    plt.grid(b=True, ls=':', color='#404040')
    plt.subplot(312)
    w = np.arange(N) * 2*np.pi / N
    plt.stem(w, a, linefmt='r-', markerfmt='ro')
    plt.title('频域信号', fontsize=15)
    plt.grid(b=True, ls=':', color='#404040')
    plt.subplot(313)
    plt.plot(x, y1, 'b-', lw=2, markersize=4, markeredgecolor='k')
    plt.title('三角波恢复信号', fontsize=15)
    plt.grid(b=True, ls=':', color='#404040')
    plt.tight_layout(1.5, rect=[0, 0.04, 1, 0.96])
    plt.suptitle('快速傅里叶变换FFT与频域滤波', fontsize=17)
    plt.show()

 实验结果：

实验结果分析：傅里叶变换是将图像从空间域转换到频率域，其逆变换是将图像从频率域转换到空间域，将图像的灰度分布函数变换为图像的频率分布函数。 频率域滤波实际上是将图像进行傅里叶变换，然后在变换域进行处理，然后进行傅里叶反变换转换回空间域，原理是用傅里叶变换表示的函数特征完全可以通过傅里叶反变换来重建，而且不会丢失任何信息（因为任何周期或非周期函数都可以表示为不同频率的正弦函数和余弦函数之和的形式）。

 

二、频率域滤波

1、频率域与空间域之间的关系

　　在已经知道了如何将图像转换到频率域，以及如何将频率域图像通过傅里叶逆变换转换回图像后，可以利用空域图像与频谱之间的对应关系，尝试将空域卷积滤波变换为频域滤波，而后再将频域滤波处理后的图像反变换回空间域，从而达到图像增强的目的，这样做的一个最主要的吸引力再域频率域滤波具有直观性的特点。

　　根据著名的卷积定律，两个二维连续函数再空间域的卷积可由其相应的两个傅里叶变换乘积的反变换而得到，反之，在频率域中的卷积可由在空间域中乘积的傅里叶变换而得到。即：

            f1(t)↔F1(ω),f2(t)↔F2(ω)

            f1(t)∗f2(t)↔F1(ω)⋅F2(ω)

2、频率域滤波的基本步骤

　首先将频率域滤波的步骤来做一个小结如下：

• 给定一幅大小为MXN的输入图像f(x,y),选择填充参数P=2M.Q=2N.
• 对f(x,y)添加必要数量的0，形成大小为PXQ的填充图像fp(x,y)

• 用(−1)x+y乘以fp(x,y)，移到其变换中心。
• 计算上图的DFT，得到F(u,v).
• 生成一个实的，对称的滤波函数H(u,v)，其大小为PXQ，中心在(P/2,Q/2)处。用阵列相乘得到乘积G(u,v)=H(u,v)F(u,v)；即G(i,k)=H(i,k)F(i,k)
• 得到处理后的图像：gp(x,y)={real[J−1[G(u,v)]}(−1)x+y        其中，为忽略由于计算不准确导致的寄生复成分，选择实部，下标p指出我们处理的是填充后的图像     

      由上述叙述可知，滤波的关键取决于滤波函数H(u,v)，常常称为滤波器，或滤波器传递函数，因为它在滤波中抑制或除去了频谱中的某些分量，而保留其他的一些频率不受影响，从而达到滤波的目的。学习重点如何通过频率域滤波来实现图像的平滑和锐化。

3、使用频率域滤波平滑图像

　　在空间域我们已经讲过图像平滑的目的及空间域平滑滤波，现在在频率域滤波中我们首先讲解三种频率平滑滤波器：理想滤波器、巴特沃斯滤波器、高斯滤波器。这三种滤波器涵盖了从非常急剧（理想）到非常平滑的滤波范围。

3.1 理想低通滤波器（ILPF)

 　　首先最容易想到得衰减高频成分得方法就是在一个称为截止频率得位置截断所有的高频成分，将图像频谱中所有高于这一截止频率的频谱成分设为0，低于截止频率的成分保持不变。如图所示（左图是其透视图，右图是其图像表示）：

 

　　

　　能够达到这种用效果的滤波器我们称之为理想滤波器，用公式表示为：H(u,v)={10 if D(u,v)≤D

                                                                                                                                     0 if D(u,v)>D0 其中，D0表示通带的半径。D(u,v)的计算方式也就是两点间的距离，很简单就能得到。

 

 

3.2 巴特沃思低通滤波器(BLPF）

　　截止频率位于距离原点D0处的n阶巴特沃斯滤波器的传递函数定义为：

        巴特沃斯滤波器的透视图及其图像显示：

 

       与理想低通滤波不同，巴特沃斯低通滤波器并没有再通过频率和滤除频率之间给出明显截止的急剧不确定性。对于具有平滑传递函数的滤波器，可在这样一点上定义截止频率，即使H(u,v)下降为其最大值的某个百分比的点。

3.3 高斯低通滤波器(GLPF)

 　　高斯低通滤波的频率域二维形式由下式给出：

                                                                              

       其中：                                                   

       是离频率矩阵中心的距离。D0是截止频率，当D(u,v)=D0时，GLPF下降到其最大值的0.607处。

　　高斯滤波器的透视图及其图像显示如下图所示：

           

3.4 实验 python实现低通滤波：

dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)

fshift = np.fft.fftshift(dft)

#设置低通滤波器

rows, cols = img.shape

crow,ccol = int(rows/2), int(cols/2) #中心位置

mask = np.zeros((rows, cols, 2), np.uint8)

mask[crow-30:crow+30, ccol-30:ccol+30] = 1

#掩膜图像和频谱图像乘积

f = fshift * mask

#傅里叶逆变换

ishift = np.fft.ifftshift(f)

iimg = cv2.idft(ishift)

res = cv2.magnitude(iimg[:,:,0], iimg[:,:,1])

#显示原始图像和低通滤波处理图像

plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original Image')

plt.axis('off')

plt.subplot(122), plt.imshow(res, 'gray'), plt.title('Low Pass Filter Image')

plt.axis('off')

plt.show()

结果：

   

实验结果分析：使低频通过而使高频衰减 ，可以有效减少图像的数据量。视觉上会有平滑、模糊的效果。
                 被低通滤波的图像比原始图像少尖锐的细节部分而突出平滑过渡部分，保留图像的整体概貌（低频部分），去掉了图像的细节（高频部分）。

4、使用频率域滤波锐化图像

　　前面已经讲过了通过衰减图像的傅里叶变换的高频成分可以平滑图像。因为边缘和其他灰度的急剧变化与高频成分有关，所以图像的锐化可在频率域通过滤波来实现，高通滤波器会衰减傅里叶变换中的低频成分而不扰乱高频信息。故我们可以考虑用高通滤波器来进行图像的锐化,一个高频滤波器是从给定低通滤波器用下式得到的:

                                                    HHP(u,v)=1−HLP(u,v)

       与低通滤波器对应，这里介绍理想高通滤波器，巴特沃斯高通滤波器，高斯高通滤波器三种高通滤波器。

4.1 理想高通滤波器 (IHPF)

　　与低通对应，理想高通滤波器定义为：

      透视图和图像显示如下：

        

4.2 巴特沃思高通滤波器 （BHPF)

 　同理n阶巴特沃斯高通滤波器的定义为：

            

    透视图和图像显示如下：

   

4.3 高斯高通滤波器（GHPF)

 　 高斯高通滤波器定义为：

                       

       透视图和图像显示如下：

    

 

4.4 实验 python实现高通滤波实验：

dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)

fshift = np.fft.fftshift(dft)

#设置高通滤波器

rows, cols = img.shape

crow,ccol = int(rows/2), int(cols/2) #中心位置

mask = np.ones((rows, cols, 2), np.uint8)

mask[crow-30:crow+30, ccol-30:ccol+30] = 0

#掩膜图像和频谱图像乘积

f = fshift * mask

#傅里叶逆变换

ishift = np.fft.ifftshift(f)

iimg = cv2.idft(ishift)

res = cv2.magnitude(iimg[:,:,0], iimg[:,:,1])

#显示原始图像和高通滤波处理图像

plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original Image')

plt.axis('off')

plt.subplot(122), plt.imshow(res, 'gray'), plt.title('High Pass Filter Image')

plt.axis('off')

plt.show()

 结果：

实验结果分析：使高频通过而使低频衰减 
                 被高通滤波的图像比原始图像少灰度级的平滑过渡而突出边缘等细节部分，保留了图像的细节，模糊了概貌。（对比空间域的梯度算子、拉普拉斯算子）

5、选择率滤波器

      在很多应用中，图像处理的目的是处理指定频段或频率矩阵的小区域，此时我们需要使用选择滤波器对其进行处理，选择滤波器分为带通滤波器和带阻滤波器和陷波器。

5.1 带阻滤波器、带通滤波器

　　所谓的带通滤波器即是将低频滤波和高频滤波相结合，最后我们可以利用带阻滤波器滤掉周期性出现的噪声，由前面可知，

理想带通滤波器公式为

 

       巴特沃斯带通滤波器公式为

 

      高斯带通滤波器公式为

 

 

     与由低通滤波器得到高通滤波器相同的方法，由带阻滤波器我们可以得到带通滤波器

 

                                                                                 HBP(u,v)=1−HBR(u,v)

5.2 实验 python实现带通滤波：

from matplotlib import pyplot as plt

#读取图像

img = cv2.imread('D:/data/collage.jpg', 0)

#傅里叶变换

dft = cv2.dft(np.float32(img), flags = cv2.DFT_COMPLEX_OUTPUT)

fshift = np.fft.fftshift(dft)

#设置带通滤波器

# w 带宽

# radius: 带中心到频率平面原点的距离

rows, cols = img.shape

crow,ccol = int(rows/2), int(cols/2) #中心位置

w = 30

radius = 30

mask = np.ones((rows, cols, 2), np.uint8)

for i in range(0, rows):

    for j in range(0, cols):

        # 计算(i, j)到中心点的距离

        d = math.sqrt(pow(i - crow, 2) + pow(j - ccol, 2))

        if radius - w / 2 < d < radius + w / 2:

            mask[i, j, 0] = mask[i, j, 1] = 0

        else:

            mask[i, j, 0] = mask[i, j, 1] = 1

#掩膜图像和频谱图像乘积

f = fshift * mask

#傅里叶逆变换

ishift = np.fft.ifftshift(f)

iimg = cv2.idft(ishift)

res = cv2.magnitude(iimg[:,:,0], iimg[:,:,1])

#显示原始图像和带通滤波处理图像

plt.subplot(121), plt.imshow(img, 'gray'), plt.title('Original Image')

plt.axis('off')

plt.subplot(122), plt.imshow(res, 'gray'), plt.title('Band Pass Filter Image')

plt.axis('off')

plt.show()

结果：

实验分析：在指定频率矩形的小区域中，图像得到了频率过滤，图像的部分细节被突出，同时，对噪声以外的成分也有衰减。

6、同态滤波

  6.1 同态滤波概念

        图像的形成是由光源的入射和反射到成像系统中来的到物体的外观特征的一个过程，假如我们用形如f(x,y)的二维函数来表示图像，则f(x,y)可以由两个分量来表示：（1）入射到被观察场景的光源照射总量（2）场景中物体所反射光的总量。这两个分量分别被称为入射分量和反射分量，可以分别表示为i(x,y)和r(x,y)。两个函数的乘积为f(x,y)

       f(x,y)=i(x,y)r(x,y)，其中0

                        F(F(x,y))≠F(i(x,y))F(r(x,y))

但是，可以借由取对数来分离入射光频率和反射光频率，假设我们定义

             z(x,y)=lnF(x,y)=lni(x,y)+lnr(x,y)

则有      F(z(x,y))=F(lnF(x,y))=F(lni(x,y))+F(lnr(x,y))

或          Z(ω,ν)=I(ω,ν)+R(ω,ν)

其中      Z,I,R分别是 z,lni(x,y)和lnr(x,y)

            g(x,y)=exp(∣hj​(x,y)∣)=exp(∣hi​(x,y∣)⋅exp(∣hr​(x,y∣)

的傅里叶变换。函数Z表示低频照明图像和高频反射图像两个图像之和的傅立叶变换,其传递函数如下所示：

如果我们现在应用具有抑制低频分量和增强高频分量的传递函数的滤波器，那么我们可以抑制照明分量并增强反射分量。从而有

                           S(ω,ν)=H(ω,ν)Z(ω,ν)=H(ω,ν)I(ω,ν)+H(ω,ν)R(ω,ν)

其中S是傅里叶变换的结果。在空间领域

                          s(x,y)=F−1(S(ω,ν))=F−1(H(ω,ν)I(ω,ν))+F−1(H(ω,ν)R(ω,ν))

由定义：           i′(x,y)=F−1(H(ω,ν)I(ω,ν))

                         r′(x,y)=F−1(H(ω,ν)R(ω,ν))

 我们有             s(x,y)=i′(x,y)+r′(x,y)

最后，因为z(x,y)是通过去输入图像的对数形成的，我们可以通过取滤波后的而结果的指数这一反处理来形成输出图像：

                        F^(x,y)=exp[s(x,y)]=exp[i′(x,y)]exp[r′(x,y)]=i0(x,y)r0(x,y)

以上便是同态滤波的整个流程，可以总结如下：

       图像的照射分量通常由慢的空间变化来表征，而反射分量往往引起突变，特别是在不同物体的连接部分。这些特性导致图像取对数后的傅里叶变换的低频成分与照射分量相联系，而高频成分与反射分量相联系。虽然这些联系只是粗略的近似，但它们用在图像滤波中是有效的。

       使用同态滤波器可更好的控制照射成分和反射成分。这种控制需要指定一个滤波器H(u，v)，它可用不同的可控方法影响傅里叶变换的低频和高频成分。

6.2 实验 python实现同态滤波实验

def homomorphic_filter(src, d0=10, r1=0.5, rh=2, c=4, h=2.0, l=0.5):
    gray = src.copy()
    if len(src.shape) > 2:
        gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
    gray = np.float64(gray) 
    rows, cols = gray.shape
    gray_fft = np.fft.fft2(gray)
    gray_fftshift = np.fft.fftshift(gray_fft)
    dst_fftshift = np.zeros_like(gray_fftshift)
    M, N = np.meshgrid(np.arange(-cols // 2, cols // 2), np.arange(-rows//2, rows//2))
    D = np.sqrt(M ** 2 + N ** 2)
    Z = (rh - r1) * (1 - np.exp(-c * (D ** 2 / d0 ** 2))) + r1
    dst_fftshift = Z * gray_fftshift
    dst_fftshift = (h - l) * dst_fftshift + l
    dst_ifftshift = np.fft.ifftshift(dst_fftshift)
    dst_ifft = np.fft.ifft2(dst_ifftshift)
    dst = np.real(dst_ifft)
    dst = np.uint8(np.clip(dst, 0, 255))
    return dst
path = "D:/data/collage.jpg"
if os.path.isfile(path):
    print("path {} is existence;".format(path))
    img = Image.open(path)
    Img = img.convert('L')
    img = np.array(img)
    print(img, img.shape)
img_new = homomorphic_filter(img)
print("new img shape is {}".format(img_new.shape))
cv2.imwrite("2.png", img_new)
 

实验结果：

实验结果分析：在频域内的同态滤波方法只要选取适当的滤波器参数，就可以在增强图像高频信息的同时保留部分低频信息，达到压缩图像灰度的动态范围， 对光照不均匀的图像的补偿效果更明显，增强图像的对比度的效果。