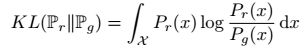Wasserstein GANs 三部曲（一）：Towards Principled Methods for Training Generative Adversarial Networks的理解
论文地址：https://arxiv.org/abs/1701.04862
这一篇文章相当于一个引言，运用了许多推导与证明说明了生成对抗网路存在的一系列问题，然后引入了一个新的评价标准。虽然公式推导是比较乏味的，也可以参阅知乎上的这篇文章https://zhuanlan.zhihu.com/p/25071913，比较简单直观。当时我在学习的时候有部分也借鉴了这篇文章，以下是我的理解：
第一部分GAN 存在的问题：
1.GAN问题：难以训练，训练过程只能是启发式的，比如之前的DCGAN
2.GAN的生成模型和其它相比并没有太大不同，最主要的不同之处就是生成模型如何训练。
3.以前的生成模型训练依赖于极大似然估计或者KL散度。
K L散度定义：
如果两个分布相等，则KL散度达到最小值。但是KL散度是不对称的，论文中是以
为例说明的，如下（一般文章中是最小化
，在分析中互换一下就可以啦）
如果
，尤其是
，那么散度变得无穷大，说明如果生成模型没能生成真实数据，cost会很大；
相反如果
尤其是
，散度趋于零，说明如果生成模型生成假数据，cost很小，但是这不是我们想要的结果。
JS散度定义：
，
为
。
4.GAN的优化目标：
令其偏导等于0，求解最优判别模型得
（GAN论文已给出），那么在判别模型达到最优时，
，也就是说最小化目标函数等同于最小化俩分布的JS散度。但是GAN之所以训练困难问题就在这里。
第二部分 解释证明稳定性以及饱和问题
1.直观上理解：
JS散度的问题：如果两个分布不重叠或者重叠部分可忽略不计，那么其JS散度达到最大值且恒为常数，这样的话梯度消失，生成模型难以训练。
那么什么算重叠部分可忽略呢？等价于说两个分布是高维空间的低维流型，那么他们就撑不满高维空间，也就是说他们在高维空间不连续，也就是说即使有重叠部分，但是在高维空间测度为0（比如说两条曲线相交于一点，这一点长度为0，长度为二维空间的测度）。
再来看GAN的两个分布，
确实是高维空间的低维流型，
是由高斯分布的Z完全决定的，因此
在高维空间一定是不连续的，他的低维流型的维度一定不大于Z的维度，所以他也是高维空间的低维流型。
2.数学推理过程：
引理1：已知
，即Z经过一系列变换成X，g(z)就可以说是一个不超过Z的度的低维流型，如果X的维度比Z高，那么g(z)在X上测度为0.
定理2.1：如果
和
有不相交的支撑集，即使很接近，则一定有一个最优判别器将其分开。
定义2.1：transversality定义，存在
，满足
（
）就说
定义2.2：完全对齐的定义，
不横截性相交，则两个分布完全对齐。
引理2：
是
的子流型，是
连续随机向量，
且
，则
两个定义和引理2旨在说明不存在两个流型是完全对齐的
引理3：M、P不完全对齐，且不是全维，令
，则
在M、P上测度为0.
定理2.2: 
，支撑集为
，则存在一个最优判别器（由引理3和定理2.1所证，详见论文）
定理2.3：在如上所述的情况下，JS散度为常数log2,KL散度为无穷大。
3.具体loss函数具体分析推理
（1）原始代价函数：
定理2.4：若
，则
引理2.1：
也就是说当判别模型D越近似于最优时，生成模型的梯度就会接近于0，以至于梯度消失。
（2）改进的cost函数：
定理2.5：
也就是说KL散度试图拉近两个分布，而JS散度试图使两个分布远离，因此会造成训练不稳定，其次KL散度的问题之前讲过，容易造成生成模型的生成样本单一化问题。
造成训练困难的本质原因，是cost函数不合理，而两个分布又是重叠可忽略不计的。
第三部分 修改
第一种修改：给两个分布加噪声使得重叠，本质未改变。
第二种修改：修改度量方法，不使用散度，使用Wasserstein距离（见第二篇论文）。