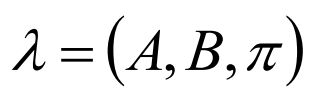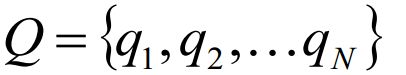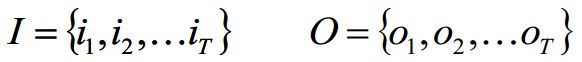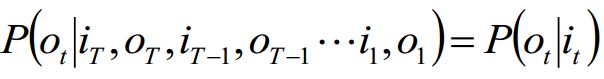HMM之模型详解

注：本文中所有公式和思路来自于邹博先生的《机器学习升级版》，我只是为了加深记忆和理解写的本文。

从本文到后边3篇文章都会介绍HMM(隐马尔科夫模型)，也就是好多80后戏称的“韩梅梅”模型，HMM模型我们可以下面的图描述一下：

HMM模型是关于时序的模型，描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列，再由各个状态生成观测序列的过程。

在上图中，z行就是不可观测的状态序列，x行就是由每个z隐变量生成的观测序列组成的观测序列。

我在之前的一篇文章《概率图模型之贝叶斯网络》中详细说过贝叶斯网络，HMM也是贝叶斯网络中的一种，我们可以将z1、z2、x1看做是一个tail-to-tail，那么只要z1是不可观测的，那么x1和z2就不是独立的，同理x1、x2也不是独立。

现在我们假设z序列的状态可以有n个状态，那么从z1转移到z2也就是有n*n种可能，所以我们可以用一个矩阵表示这个转移过程，将这个矩阵叫做状态转移矩阵A，每个状态又可以生成一个观测值，假定观测值有m种，那么我们也用一个矩阵表示这个发射过程，将这个矩阵叫做发射矩阵/观测矩阵B，在这个时序最开始我们我还还需要给定一个初始的状态转移概率，也就是z1是某个状态的概率，我们用一个向量π表示。

那么这个模型我们就可以用一个三元组表示：

模型描述完了，接着我们该用符号表示一下了，我们设定：

Q是所有可能的状态的集合：

V是所有可能的观测的集合：

I是长度为T的状态序列，O是对应的观测序列：

A是状态转移概率矩阵，其中N可能的状态数，并且我们要求A一定要是离散的，这是HMM的一个前提：

其中αij是在时刻t出于qi状态的前提下，在t+1时刻转移到qj状态的概率：

B是观测矩阵，其中M为可能的观测数：

其中bik是在时刻t处于qi状态的前提下，生成的观测vk的概率：

π是初始状态转移概率向量：

其中πi表示在时刻1处于状态qi的概率：

到这里我们刚刚将HMM的参数介绍完，其实没有任何难度，就是比较多而已，只要了解HMM模型的结构和生成过程，这些都是洒洒水。

接着我想说一下HMM的两个性质，其实蛮重要的我觉得：

1. 齐次假设：

2. 观测独立性假设：

我们来理解一下这两个假设：其实就是我在前文已经提到的，

齐次假设：本质就是时刻t的状态为qi，原本是要给定t时刻之前的所有状态和观测才可以确定，但是其实我们给出前一个时刻t-1的状态就可将t时刻与之前隔断，也就是说我们假设t时刻与t-1之前的所有状态和观测是独立的。

观测独立性假设：本质就是t时刻的观测为ot，原本是要给定包括t时刻和t时刻之前所有的观测和状态才能确定，现在我们给定t时刻状态qi就将ot与前边隔断，也就是说我们假设t时刻的观测ot与t时刻之前的所有状态和观测是独立的

为啥说这么一个鬼性质呢？其实我们在后边的推导默认使用该假设，另外我们也可以根据这两个性质来看看某个系统是不是可以用HMM来建模，就是这么个小事情而已，感觉不好理解跳过也可。

我们可以把之前讲的这些都看成开胃小菜，后边就要上正菜了，但是小菜同样重要，没有小菜开胃正菜是吃不舒服的。。。。

HMM的三个基本问题：

概率计算问题：前向-后向算法----动态规划

给定模型 λ = (A, B, π)和观测序列O={o1, o2, o3 ...}，计算模型λ下观测O出现的概率P(O | λ)

学习问题：Baum-Welch算法----EM算法

已知观测序列O={o1, o2, o3 ...}，估计模型λ = (A, B, π)的参数，使得在该参数下该模型的观测序列P(O | λ)最大

预测问题：Viterbi算法----动态规划

解码问题：已知模型λ = (A, B, π)和观测序列O={o1, o2, o3 ...}，求给定观测序列条件概率P(I | O，λ)最大的状态序列I

为了让文章别太长，我将HMM的全部介绍分为4部分，后边三篇将介绍上面提到的三个问题，欢迎批评指正。