前言
排序是重新排列一系列对象以便按照某种逻辑顺序排列的过程。排序在商业数据处理和现代科学计算中起着重要作用。在交易处理,组合优化,天体物理学,分子动力学,语言学,基因组学,天气预报和许多其他领域中的应用比比皆是。
在本章中,我们考虑了几种经典的排序方法和一种称为优先级队列的基本数据类型的有效实现。我们讨论比较排序算法的理论基础,并结合本章应用排序和优先级队列算法。
2.1 基本排序引入了选择排序,插入排序和 shellort。
2.2 Mergesort 描述了megesort,一种保证在线性时间内运行的排序算法。
2.3 Quicksort 描述了quicksort,它比任何其他排序算法使用得更广泛。
2.4 优先级队列引入优先级队列数据类型和使用二进制堆的有效实现。它还引入了 heapsort。
2.5 应用程序描述了排序的应用程序,包括使用备用排序,选择,系统排序和稳定性
排序介绍
进行排列我们应该遵循哪些规则呢?让我们先看看典型基本排序问题。
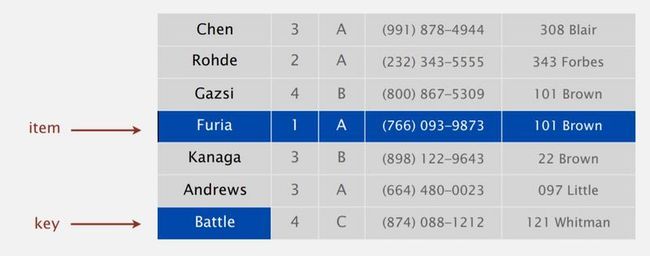
比如,大学有很多学生档案,对于每个学生有一些信息,可能是姓名、班级编号、成绩、电话号码、地址。
我们查看一个元素,那个元素有一条记录,这个记录就是我们要排序的信息,准确地说,记录中有一部分叫做关键字 (key),
我们将记录根据关键字进行排列,这就是排序问题。
下图将数组中的 n 个元素根据元素中的定义的关键字 (此为姓) 升序排列
排序的应用:
排序的应用很多,比如快递的包裹,纸牌游戏,手机联系人,图书馆的图书编号等等。我们的目标是能够对任何类型的数据进行排序。
来看几个客户端程序。
实例:排序客户端
例1:对字符串进行排序
public class StringSorter
{
public static void main(String[] args)
{
String[] a = StdIn.readAllStrings();
Insertion.sort(a);
for (int i = 0; i < a.length; i++)
StdOut.println(a[i]);
}
}这个例子中:
- 用 readString() 方法从文件中读取字符串。
- 这个方法在我们的 StdIn 类里,需要一个文件作为参数,将第一个命令行参数作为文件名,从文件中读取一个字符串数组,字符串以空白字符分隔,接下来又调用 Insertion.sort() 方法。
- Insertion.sort 这个方法以数组 a 作为第一个实参,然后将数组中的字符串排序
这个例子中,words3.txt 有一些单词,这个客户端输出的结果就是这些单词重新按照字母表的顺序排序的结果。
% more words3.txt
bed bug dad yet zoo ... all bad yes
% java StringSorter < words3.txt
all bad bed bug dad ... yes yet zoo
[suppressing newlines]例2. 将一些随机实数按升序排序
public class Experiment
{
public static void main(String[] args)
{
int n = Integer.parseInt(args[0]);
Double[] a = new Double[n];
for (int i = 0; i < n; i++)
a[i] = StdRandom.uniform();
//调用插入排序方法
Insertion.sort(a);
for (int i = 0; i < n; i++)
StdOut.println(a[i]);
}
}这个客户端程序调用插入排序方法。它从标准输入中读取数字,放进数组,然后调用 Insertion.sort(插入排序),最后打印输出。
下边的打印输出的数字是从小到大排好序的。这看起来有点像人为设计的输入,也有很多应用中可以用随机输入作为好的输入模型。
% java Experiment 10
0.08614716385210452
0.09054270895414829
0.10708746304898642
0.21166190071646818
0.363292849257276
0.460954145685913
0.5340026311350087
0.7216129793703496
0.9003500354411443
0.9293994908845686例3. 对文件排序
import java.io.File;
public class FileSorter
{
public static void main(String[] args)
{
File directory = new File(args[0]);
File[] files = directory.listFiles();
Insertion.sort(files);
for (int i = 0; i < files.length; i++)
StdOut.println(files[i].getName());
}
}% java FileSorter .
Insertion.class
Insertion.java
InsertionX.class
InsertionX.java
Selection.class
Selection.java
Shell.class
Shell.java
ShellX.class
ShellX.java这个例子中,给定目录中的文件名,我们要对文件排序。这次又用到了Java的File文件类。
- 我们用这个类中的 listFiles() 方法获得包含给定目录中所有文件名的数组。
- Insertion.sort() 使用这个数组作为第一实参。
- 同样,程序对这些文件名进行了排序,然后依次将文件名以字母表的顺序打印输出
这是三个不同的客户端,对应三种完全不同类型的数据。
任务的第一条规则:我们要考虑如何才能完成实现一个排序程序,可以被三个不同的客户端用来对三种不同数据类型排序。
这里采取的方式是一种叫做回调的机制。
回调机制 Callbacks
我们的基本问题是:在没有元素关键字类型的任何信息的情况下如何比较所有这些数据。
答案是我们建立了一个叫做回调的机制
Callback = 对可执行代码的引用
- 客户端将对象数组传递给排序函数sort()
- sort() 方法根据需要调用 object 的比较函数 compareTo()
实现回调的方式:
有很多实现回调函数的办法,和具体编程语言有关。不同的语言有不同的机制。核心思想是将函数作为实参传递给其他函数。
涉及到函数式编程思想,需要更深的理论,可以追溯到图灵和彻奇。
・Java: interfaces.
・C: function pointers.
・C++: class-type functors.
・C#: delegates.
・Python, Perl, ML, Javascript: first-class functions.
Java中,有一种隐含的机制,只要任何这种对象数组具有 compareTo() 方法。排序函数就会在需要比较两个元素时,回调数组中的对象对应的compareTo()方法。
回调:Java 接口
对于Java,因为要在编译时检查类型,使用了叫做接口的特殊方法。
接口 interfaces:一种类型,里头定义了类可以提供的一组方法
public interface Comparable-
{
//可以看作是一种类似于合同的形式,这个条款规定:这种方法(和规定的行为)
public int compareTo(Item that);
}
实现接口的类:必须实现所有接口方法
public class String implements Comparable//String 类承诺履行合同的条款
{
...
public int compareTo(String that)
{
// 类遵守合约
...
}
} "签署合同后的影响":
- 可以将任何 String 对象视为 Comparable 类型的对象
- 在Comparable对象上,可以调用(仅调用)compareTo() 方法。
- 启用回调。
后面我们会详细介绍如何用Java接口实现回调。这个比较偏向编程语言的细节,但是确实值得学习,因为它使我们能够以类型安全的方式使用为任何类型数据开发的排序算法。
回调:路线图

注:key point: no dependence on type of data to be sorted 关键点:不依赖于要排序的数据类型
我们已经看了一些客户端程序。这是那个对字符串进行排序的客户端程序 (上边的例1)。
- 客户端以某类型对象数组作为第一实参(Comparable[] a),直接调用 sort() 方法。
- Java中内置了一个叫做Comparable(可比较的)的接口 ( java.lang.Comparable interface )
- Comparable 接口规范要求实现 Comparable 的数据类型要有一个compareTo()方法。这个方法是泛化的,会对特定类型的元素进行比较
public interface Comparable- {public int compareTo(Item that);}
- 当我们实现要排序的对象(这里为String )时我们就实现 Comparable 接口
public class String implements Comparable
因为排序是在很多情形中要使用的操作,Java标准库中会用到排序的类型很多都实现了Comparable接口,意味着,这些数据类型具有实现 compareTo()方法的实例方法。它将当前对象 (a[j]) 与参数表示的对象 (a[j-1]) 相比较,根据具体的一些测试返回比较的结果,比如
返回 -1 表示小于;返回 +1 表示大于;返回0表示相等,排序算法的实现就只需要这么一个compareTo()方法。
在函数声明的时候,它要求参数必须是 Comparable 类型数组 (Comparable[] a),这意味着数组中的对象需要实现 Comparable 接口,或者说对象必须有compareTo() 方法,然后排序代码直接使用 compareTo() 对一个对象实例 (a[j]) 调用这个方法, 以另一个对象实例 (a[j-1]) 作为实参。
在这个例子中测试第一个是否小于第二个。关键在于排序实现与数据类型无关,具体的比较由 Comparable 接口处理,不同类型的 Comparable 数组最终会以相同的方式排序,依赖于接口机制,回调到实际的被排序对象类型 (String) 的 compareTo() 代码。
全序关系 total order
compareTo() 方法实现的是全序关系(total order)
全序关系整体来说就是元素在排序中能够按照特定顺序排列。
全序关系是一种二元关系 ≤ 满足:
- 反对称性 Antisymmetry :v ≤ w 并且 w ≤ v 则这种情况成立的唯一可能是 v = w
- 传递性 Transitivity:v ≤ w 并且 w ≤ x,则 v ≤ x
- 完全性 Totality:要么 v ≤ w ,要么 w ≤ v,要么 v = w (没有其他情况了)
有几条很自然的规则,有三个性质:
我们一般考虑作为排序关键字的很多数据类型具有自然的全序关系,如整数、自然数、实数、字符串的字母表顺序、日期或者时间的先后顺序等等
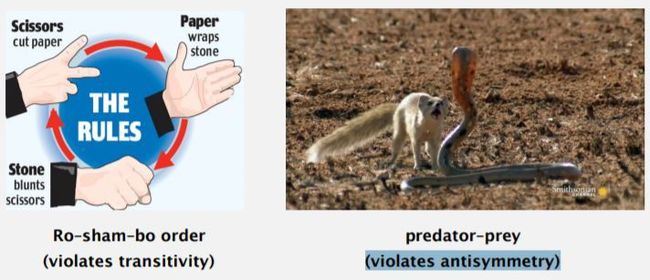
但不是所有的有序关系都是全序关系。
比如石头、剪刀、布是不具有传递性。如果已知 v ≤ w,w ≤ x,你并不一定知道 v 是否 ≤ x
还有食物链也是,违反了反对称性
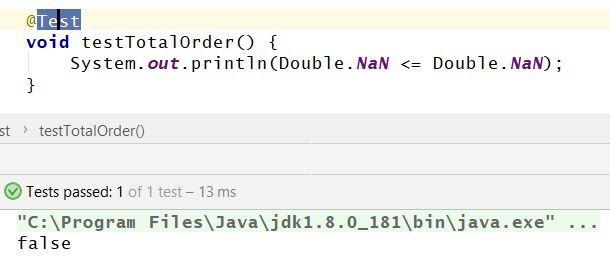
Surprising but true. The <= operator for double is not a total order. (!)
Comparable API
按照 Java 中的规定我们需要实现 compareTo() 方法,使得 v 和 w 的比较是全序关系。
而且按照规定:
- 如果是小于,返回负整数
- 如果相等返回0
- 如果当前对象大于作为参数传入的对象则返回正整数。
- 如果对象类型不相容,或者其中一个是空指针,compareTo() 会抛出异常
Java 内置的可比类型:Java中很多数字、日期和文件等等标准类型按照规定都实现了 compareTo() 方法
自定义可比类型:如果我们自己实现的类型要用于比较,就要根据这些规则,自己去实现 Comparable 接口
Comparable 接口的实现
实现一般是直截了当的。这里有个例子,这是Java中实现的 Date 日期数据类型的简化版,我们用来演示实现Comparable接口
//在类声明之后,我们写implements Comparable 然后在泛型类型填上类名,因为我们后面只允许日期类型与其他日期类型比较
public class Date implements Comparable
{
//Date类有三个实例变量: month,day,year
private final int month, day, year;
//构造函数通过参数设置这些变量
public Date(int m, int d, int y)
{
month = m;
day = d;
year = y;
}
public int compareTo(Date that)
{
if (this.year < that.year ) return -1;
if (this.year > that.year ) return +1;
if (this.month < that.month) return -1;
if (this.month > that.month) return +1;
if (this.day < that.day ) return -1;
if (this.day > that.day ) return +1;
return 0;
}
} 如果想要比较两个不同的日期,首先是检查 this.year 是否小于 that.year, 当前日期对象和作为参数的日期对象的年份进行对比, 如果为“真”那么就是小于,返回-1。如果 this.year 更大,返回+1 否则,年份就是相同的,那么我们就必须检查月份来进行比较, 这样一直比较到日期。只有三个变量完全相同才返回0.
这个例子实现了 Comparable 接口, 实现了compareTo()方法,可以将日期按照你期望的顺序排列。
两个有用的排序抽象方式
Java语言为我们提供了Comparable接口的机制,使我们能够对任何类型数据排序。当我们后续实现排序算法时,我们实际上将这个机制隐藏在我们的实现下面。
我们采用的方式是将引用数据的两个基本操作:比较和交换,封装为静态方法
Less. Is item v < w ?
private static boolean less(Comparable v, Comparable w)
{ return v.compareTo(w) < 0; }方法 less() 以两个 Comparable 对象作为参数,返回 v.compareTo(w) < 0.
Exchange. Swap item in array a[] at index i with the one at index j.
private static void exch(Comparable[] a, int i, int j)
{
Comparable swap = a[i];
a[i] = a[j];
a[j] = swap;
}当我们对数组中的元素进行排序时另一个操作是 swap,将给定索引 i 的对象与索引 j 的对象交换.
这个操作是每个程序员学习赋值语句的入门语句,将 a[i] 保存在变量 swap 中,a[j] 放进 a[i],然后 swap 放回到 a[j]
我们的排序方法引用数据时只需要使用这两个静态方法。这么做有个很充分的理由。
举个例子,假设我们想检验数组是否是有序的。这个静态方法中如果数组有序,则返回“真”,无序则返回“假”。
这个方法就是从头至尾过一遍数组,检查每个元素是否小于前一个元素。如果有一个元素比前一个元素小,那么数组就是无序的,返回“假”。如果直到数组结尾也没有检测到,那么数组是有序的。非常简单的代码。
选择排序
第一个基本排序方法很简单,叫做选择排序。
算法介绍
选择排序的思想如下:从未排序数组开始,我们用这些扑克牌举例,在第 i 次迭代中,我们在数组剩下的项中找到最小的,这个情况下,2 是所有项中最小的,然后,我们将它和数组中的第一项交换,这一步就完成了。
选择排序就是基于这样的思想迭代操作。
基本的选择排序方法是在第 i 次迭代中,在数组中第i项右边剩下的或者索引比 i 更大的项中找到最小的一项,然后和第 i 项交换。
开始 i 是 0,从最左端开始扫描所有右边剩下的项,最小的是2,右起第3项,那么我们把第 i 项和最小项交换,这是第一步。
i左边部分的数组就是排过序的。然后 i + 1,继续重复的操作。
i + 1 为了寻找最小的项都要扫描全部剩下的项,但一旦找到之后,只需要交换两张牌,这就是选择排序的关键性质。
最后 8 是最小的,这时,我们知道已经是有序的了,但是程序不知道,所以必须检查并且做决定。i 和 min 相同,自己和自己交换,最后一次迭代。这个过程结束后,我们知道整个数组已经是最终状态,是有序的了。
理解算法工作方式的一个办法是考虑其不变性。
对于选择排序,我们有个指针,变量 i,从左到右扫描。 假设我们用箭头表示这个指针,如下图, 不变式就是:
- 箭头左边的项不会再变了,它们已经是升序了
- 箭头右边的项都比箭头左边的项大,这是我们确立的机制
算法通过找到右边最小的项,并和箭头所指的右边下一项交换来维持不变性。
Java实现
为了维持算法的不变式,我们需要:
- 向右移动指针 i 加 1
- 在指针的右边找到最小的索引
- 交换最小索引与当前指针的值
向右移动指针 i 加1后,不变式有可能被破坏,因为有可能在指针右边有一个元素比指针所指的元素小导致不变式被破坏,我们要做的是找到最小项的索引,然后交换,一旦我们完成了交换,我们又一次保留了不变式。这时指针左边元素不会再变了,右边也没有更小的元素,这也就给出了实现选择排序的代码。
基础实现
实现不变性的代码如下:
import edu.princeton.cs.algs4.StdIn;
import edu.princeton.cs.algs4.StdOut;
public class Selection {
public static void sort(Comparable[] a) {
int n = a.length;
for (int i = 0; i < n; i++) {
//在指针右边找到最小项
int min = i;
for (int j = i + 1; j < n; j++)
if (less(a[j], a[min]))
min = j;
//交换最小索引与当前指针的值
exch(a, i, min);
}
}
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.print(a[i]);
}
}
//写一个超简单的客户端
public static void main(String[] args) {
String[] a = {"1","5","3","8","4","1","4","5"};
Selection.sort(a);
show(a);
}
}我们将数组的长度记为 n, for循环遍历数组中每个元素变量, min用来存储指针 i 右边最小元素的索引, 内层的 j 的for循环,如果找到更小的值,则重设min 一旦检查完 i 右侧所有的元素,将最小的和第 i 项交换, 这就是选择排序的完整实现。
泛型方法
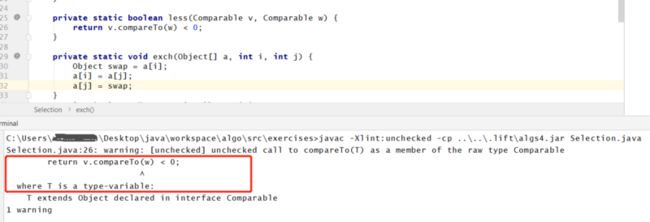
值得注意的是当我们尝试编译的时候会出现如下警告:
发生的原因:
实质上,此警告表示 Comparable 对象无法与任意对象进行比较。 Comparable
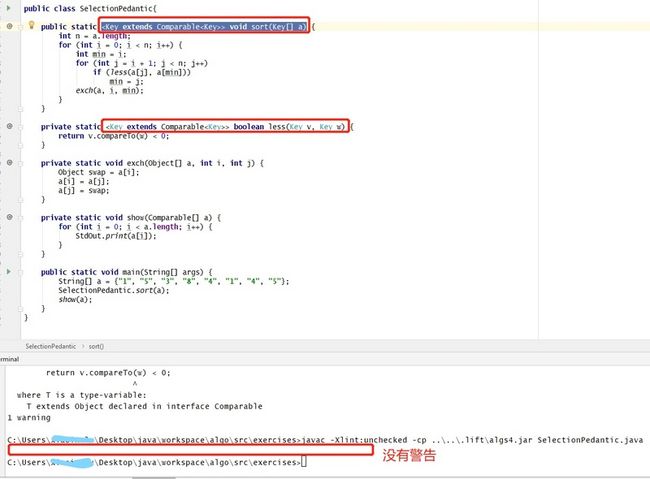
因此,为了正确使用Comparable
public class SortedList> {
public void add(T obj) { ... }
...
} 所以我们的代码要改成没有编译警告的类型安全的版本:
算法分析
为选择排序的开销建立数学模型非常容易.
命题:选择排序使用大约 n^2 / 2 个比较以及,整 n 次交换。
- (n – 1) + (n – 2) + ... + 1 + 0 ~ n^2 / 2
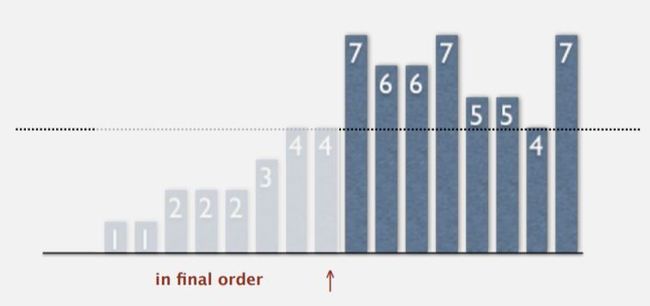
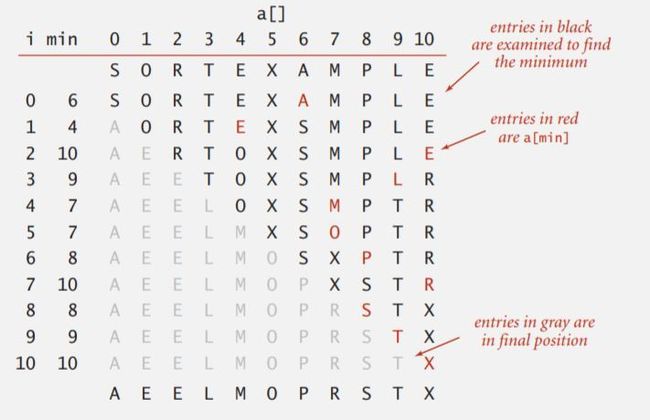
只要看看这个选择排序运行的跟踪记录,这就是这个命题的图形证明。
图中:
- 黑色的项是每次为了寻找最小项检查的项
- 最小项是红色的
- 灰色的项是未检查的项,已经在最终位置了
你可以看到这基本就是 n x n 的正方形,其中大约一半的元素是黑色的,即大约 n^2 / 2,你也能看出准确的表达式(n – 1) + (n – 2) + ... + 1 + 0, 就是总共比较的次数。然后在变量 i 的这 n 个取值各有一次交换,所以这是交换次数的开销。
- 关于选择排序的这个命题说明了很有意思的一点,就是它和输入的序列本身的顺序无关。
- 选择排序需要平方时间因为它总要查看所有的项寻找最小项
- 另一个性质就是要完成排序这已经是移动开销最小的了,选择排序只需要线性次数的交换
每一项都是仅仅一次交换就放在了最终位置。
选择排序指针由左至右扫描,每次扫描找到右边最小的项,交换到它最终的位置上。如果数组一部分已经排好序了,这对选择排序不影响,依然要一遍一遍扫描,即使是完全有序的,依然要扫描右边的项来找最小的元素。这就是选择排序,我们第一个基本排序方法
Q. 如果数组已经排好序,那么插入排序比较需要多少次?
- 对数级
- 线性级
- 平方级
- 立方级别
A. 查看附录
插入排序
插入排序,这是另外一种基本排序方法,有趣的是 相比选择排序插入排序具有相当不同的性能。
算法介绍
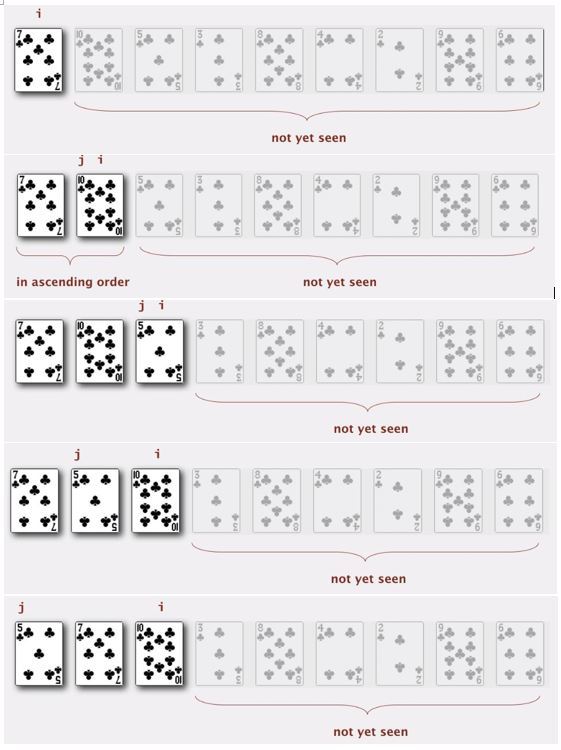
下边是一个插入排序的演示。对于插入排序,我们要做的和之前一样,从左到右移动索引 i,但现在,在第 i 个迭代中 我们将会把 a[ i ] 移动到其左侧的位置,让我们用牌的示例来看看这是怎么工作的。
现在我们从初始化 i 为第一张牌开始,我们的想法是 i 的左边的所有纸牌将会被排序,右边的纸牌,我们全部先都不去看
所以,i 左侧所有的纸牌是升序,右侧所有的纸牌我们现在还没检查过,第二步我们增加 i ,在这种情况下指针左边已经排好序了,我们什么也不用做。
当 i 是数组中的第三项时,此时我们从索引 j 开始,然后,j 从 i 开始向左边移动,我们要做的是将5与它左边更大的元素交换,那么,首先与10交换,依然没有到最终位置,所以再和7交换,现在已经到数组最前面了,一旦我们检查完左侧所有项或者找到一个更小的元素,i 左边所有项就排好序了
一旦完成之后,从 i 开始它左侧的数组就是升序的,i 左边就都排好序了,所以这个情形中我们用更少的工作量就完成了排序,并不总是需要一直检查到数组的开头
Java 实现
我们再从不变式的角度来看插入排序
- 指针依然是从左至右扫描,
- 指针左边的所有元素,包括指针指向的元素,都是排好序的
- 而右边的元素都还完全没有检查过
我们来看随着指针递增维持不变式的代码
将指针向右侧移动,增加 1,因为指针指向的元素没排过序,所以破坏了不变式,那么为了维持不变式, 要将它排序,需要将它和左边每个更大的元素交换。下面的代码完成的就是这个, 索引 j 从 i 开始,逐渐变小, j 指向的元素与左边的元素交换, a[j] 与左边的元素 a[j-1] 交换, 只要a[j]小于 a[j-1] 并且 j > 0 就一直交换, 我们就马上得到了插入排序的代码。
import edu.princeton.cs.algs4.StdOut;
public class InsertionPedantic {
public static > void sort(Comparable[] a) {
int n = a.length;
for (int i = 0; i < n; i++)
for (int j = i; j > 0; j--)
// a[j] 与左边的元素 a[j-1] 交换, 只要a[j]小于 a[j-1] 并且 j > 0 就一直交换
if (less(a[j], a[j - 1]))
exch(a, j, j - 1);
else break;
}
// 以下代码与选择排序一样
private static > boolean less(Key v, Key w) {
return v.compareTo(w) < 0;
}
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.print(a[i]);
}
}
public static void main(String[] args) {
String[] a = {"1", "5", "3", "8", "4", "1", "4", "5"};
InsertionPedantic.sort(a);
show(a);
}
}
与选择排序的代码类似,而且一样简单,有两个嵌套的for循环,选择排序也是一样,循环中需要进行一次检查,一次比较大小,和一次交换。这是基本排序方法的一个良好的实现。
算法分析
插入排序更复杂一些,我们的命题是:
对具有不同关键值的随机序列排序,
Average case 平均情况:插入排序平均需要使用大约 1/4 n^2 次比较, 与大约相同的 1/4 n^2 的交换次数。
这个要证明的话更复杂一些,和随机顺序的数组有关。和选择排序的证明一样,从这个 nxn 的算法步骤中, 你可以找到命题来源的思路。
黑色的元素依然是我们比较的,实际上,也是进行交换的。红色的是到达的最终位置。
你可以看到对于随机顺序的大数组,要移动到最终位置平均要移动大约一半的位置,这意味着对角线以下的元素,平均一半是黑色的 对角线以下的元素有1/2 n^2 个 一半就是1/4 n^2 精确的分析比这个详细不了多少,这个步骤更多,下图再次显示排序过程中对比和交换的操作涉及到对角线下大约一半的元素。
因为 1/4 n^2 和 1/2 n^2 相比小一半, 插入排序的速度大约是选择排序的两倍, 所以相同时间内演示中我们能够对大约两倍的元素进行排序
插入排序运行时间取决于数据开始的顺序。
我们来看看最好与最坏的情况,当然这些都是异常的情况:
Best case:
如果数组恰好已经排好序了,插入排序实际上只需要验证每个元素比它左边的元素大,所以不用进行交换,只需要 n-1 次比较就能完成排序工作。
Worst case:
如果数组是降序排列的,并且不存在重复值,每个元素都移动到数组开头那么就需要进行1/2 n^2 次比较与1/2 n^2 次交换
所以第一种情况下,插入排序比选择排序快得多, 是线性时间的而不是平方时间的, 而第二种情形中,比选择排序慢,因为需要一样的比较次数,但是多得多的交换次数。元素降序排列的情况,每次得到一个新元素,都必须一直交换到最开头。这是实际应用中我们不想见到的最坏的情况。
但也有好的情况,在很多实际应用中我们都在利用这一点,就是数组已经部分有序的情况,用定量的方法考虑问题。
部分有序数组
我们定义:一个“逆序对”(inversion)是数组中乱序的关键值对
例如:
A E E L M O T R X P S
其中有6个逆序对:T-R T-P T-S R-P X-P X-S
- T和R是乱序的,因为R应该在T的前面 T和P是乱序的,等等
我们定义:如果一个数组的逆序对数量是线性的(或者说逆序对的数量 ≤ cn, 其中 c 代表一个常数),那么这个数组是部分有序的。
部分有序的数组在实际应用中经常遇到,例如有一个大数组是有序的,只有最后加上的几个元素是无序的,那么这个数组就是部分有序的;
或者另外的情况,只有几个项不在最终位置,这个数组也是部分有序的。
实际应用中经常出现这样的情况,插入排序有意思的地方在于对于部分有序的数组。
我们定义:插入排序在部分有序数组上的运行时间是线性的
证明:
- 就是交换的次数与逆序对的个数相等 (没交换一次,逆序对就减少一个)
- 比较的次数 ≤ 交换的次数 + (n-1) (可能除了最后一个元素,在每次迭代中,一次比较会触发一次交换)
算法改进
Binary insertion sort
使用二分查找来找出插入点
-
对比所需要的次数 ~ nlgn (lg 以 2 为底)
- 但是访问数组的次数依旧是平方级的
这就是插入排序 我们学习的第二个基本排序方法。
Q. 如果数组已经是升序排好的,那么插入排序将进行多少次比较?
- 常数次
- 对数次
- 线性次
- 平方级次
A. 见附录
Shellsort 希尔排序
算法介绍
希尔排序的出发点是插入排序。插入排序有时之所以效率低下是因为每个元素每次只向前移动一个位置,即使我们大概知道那些元素还需要移动很远。
希尔排序的思想在于每次我们会将数组项移动若干位置(移动 h 个位置),这种操作方式叫做对 数组进行 h-sorting (h - 排序)。
所以h-sorted array h-有序的 数组 包含 h 个不同的交叉的有序子序列。
例如,这里 h = 4,如果从 L 开始,检查每第四个元素 - M,P,T - 这个子数组(L M P T)是有序的,
从第二个位置 E 开始,检查每第四个元素,- H, S, S - 是有序的...
这里一共有4个交叉的序列,这个数组 是经过 h-sorting 后的 h-sorted 数组,这里即是数组 {L E E A M H L E P S O L T S X R} 是经过 4-排序 后的 4-有序 的数组。
我们想用一系列递减 h 值的 h-排序 实现一种排序方法,这种排序方法由希尔(Shell)于1959年发明,是最早的排序方法之一。
又一例子:
这个例子中,从这里所示的输入 {S H E L L S O R T E X A M P L E} 开始,首先进行13-排序,移动几个项,然后是 4-排序,移动的项多了一些,最后,1-排序。
这种算法的思想在于每次排序的实现基于前面排过序的序列,只需要进行少数几次交换。
Q. 那么首先我们怎样对序列进行 h-排序呢?
A. 实际上很简单, 直接用插入排序,但是之前是每次获取新的项往回走一个,现在往回走 h 个,所以代码和插入排序是一样的,只不过顺着数组往回查看的时候之前每次只退1个,现在跳 h 个。这就是对数组进行h-排序的方法。
这里我们使用插入排序的原因基于我们对插入排序原理的理解有两点:
- 首先是如果增量 h 很大。那么进行排序的子数组长度就很小,包括插入排序在内的任何排序方法都会有很好的性能
- 另一点是如果增量小,因为我们之前已经用更大的h值进行了 h-排序,数组是部分有序的,插入排序就会很快
用选择排序作为 h-排序 的基础就不行,因为无论序列是什么顺序,它总需要平方时间,数组是否有序对选择排序没有任何影响。
我们看一个希尔排序的例子,增量是7、3、1
下图每一行的标注了红色的项就是本次迭代中发生过移动的项
- 我们从 input 序列开始,先对它进行7-排序,进行的就是插入排序,只不过每次回退7。如果是增量是 7,也就是两个元素间隔 6 个元素这么取子序列,有4个子序列,各只包含2个元素。
- 然后进行3-排序。因为已经进行过7-排序,进行 3-排序 的元素要么已经在最终位置,要么只需要移动几步。这个例子中,只有 A 移动了两步。
- 然后进行 1-排序,因为数组已经经过 7-排序 和 3-排序,需要进行 1-排序 时,数组已经基本有序了,大多数的项只移动一两个位置。
所以我们只需要进行几次额外的高增量排序,但是每个元素都只向它们的最终位置移动了几次,这是希尔排序的高效之处。实际上一旦进行了 1-排序,就是进行了插入排序,所以最终总能得到正确排序的结果。唯一的区别就是能有多高效
对希尔排序更直观的理解可以通过数学证明。如果序列经过 h-排序的,用另一个值 g 进行 g-排序,序列仍然是 h-有序的。
一个 h-有序的 数组是 h 交错排序后的子序列。
我们的命题:h-有序的 数组经过 g-排序 后依然是 h-有序的
如下图:
3-sort[] = {A E L E O P M S X R T} 是数组 a[] = {S O R T E X A M P L E} 经过 7-排序 后,再经过 3-排序 后的数组,
3-sort[] 肯定是 7-有序的 数组,当然也是 3-有序的,对7,3排序后得的序列 {A E L E O P M S X R T} 进行观察, 每向右移动7位:
{A-S},{E-X},{L-R},{E-T}都是升序的,所以 3-sort[] 是 7-有序的 数组.
这就是那些看起来很显然但是如果你试着证明它,会比你想的复杂一些的命题之一 -_-||, 而大多数人将这一点认定为事实,这是希尔排序高效之处。
步长序列
另一个问题就是对于希尔排序我们应当使用哪种步长序列.
首先能想到的想法可能是试试2的幂, 1, 2, 4, 8, 16, 32, ...实际上这个行不通,因为它在进行1-排序之前不会将偶数位置的元素和奇数位置的元素进行比较,这意味着性能就会很差。
希尔自己的想法是尝试使用2的幂减1序列,1, 3, 7, 15, 31, 63, …这是行得通的。
Knuth在60年代提出用 3x+1 的增量序列,如 1、4、13、40、121、364等,这也不错
我们使用希尔排序的时候,我们首先找到小于待排序数组长度最大的增量值,然后依照递减的增量值进行排序。但是寻找最好的增量序列是一个困扰了人们相当长时间的研究问题。
这是 Sedgewick 教授(这门课的主讲老师之一)经过大概一年的研究得出的增量序列,1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905, …
(该序列的项来自 9 x 4^i - 9 x 2^i + 1 和 2^{i+2} x (2^{i+2} - 3) + 1 这两个算式。这项研究也表明 “ 在希尔排序中是最主要的操作是比较,而不是交换。”
用这样步长序列的希尔排序比插入排序要快,甚至在小数组中比快速排序和堆排序还快,但是在涉及大量数据时希尔排序还是比快速排序慢。这个步长序列性能也不错,但是无法得知是否是最好的
Java 实现
这是用Java实现的希尔排序,使用 Knuth 的 3x+1 增量序列
import edu.princeton.cs.algs4.StdOut;
public class Shell {
/**
* 对数组进行升序排序
* @param 需要排序的数组
*/
public static > void sort(Key[] a) {
int n = a.length;
// 3x+1 increment sequence: 1, 4, 13, 40, 121, 364, 1093, ...
int h = 1;
while (h < n/3) h = 3*h + 1;// 至于为什么是 h < n/3 请查看附录
while (h >= 1) {
// 对数组进行 h-排序 (基于插入排序)
for (int i = h; i < n; i++) {
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h) {
exch(a, j, j-h);
}
}
assert isHsorted(a, h);
// 计算下一轮排序使用的增量值
h /= 3;
}
/**
* assert [boolean 表达式]
* 如果[boolean表达式]为true,则程序继续执行。
* 如果为false,则程序抛出AssertionError,并终止执行。
* assert [boolean 表达式]:'expression'
*/
assert isSorted(a);
}
// is v < w ?
private static > boolean less(Key v, Key w) {
return v.compareTo(w) < 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
// 检查数组是否已排好序
private static > boolean isSorted(Key[] a) {
for (int i = 1; i < a.length; i++)
if (less(a[i], a[i-1])) return false;
return true;
}
// 检查数组是否是 h-有序的?
private static > boolean isHsorted(Key[] a, int h) {
for (int i = h; i < a.length; i++)
if (less(a[i], a[i-h])) return false;
return true;
}
// 打印数组到标准输出
private static void show(Comparable[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.print(a[i]);
}
}
// 简单客户端
public static void main(String[] args) {
String[] a = {"1","5","3","8","4","1","4","5"};
Shell.sort(a);
show(a);
}
}
我们直接计算小于 n/3 的最大增量, 然后以那个值开始,比如从 364 开始,需要计算下一个增量时,直接 364 整除 3 等于 121,121 整数除 3 等于 40 等。这句 h = h / 3 计算下一轮排序使用的增量值。
实现就是基于插入排序。进行插入时 i 从 h 开始,然后 j 循环,每次 j 减小 h,不然代码就和插入排序一模一样了。所以,只需要给 h-排序 加上额外的循环计算插入排序的增量,代码变得稍微复杂了一些,但是对于大数组运行起来,Shell排序的效率要比插入排序高得多。
随着h值递减,每次 h-排序 后数组越来越有序
算法分析
对于 3x+1 的增量序列最坏情况下比较的次数是 O(N^3/2),实际应用中比这个小得多。
问题是没有精确的模型能够描述使用任何一种有效的增量序列的希尔排序需要进行比较的次数。
下图是通过 Doubling hypothesis 方法,简单说就是翻倍输入的方法对希尔排序的性能试验得出的结果 与 推断的函数模型计算值的对比
- N:原始输入数据的大小;compares:对应的输入需要通过多次比较得到完全有序数组;
N^1.289: 对应输入大小的1.289次幂;2.5 N lg N:对应输入的对数计算值
希尔排序的比较次数是 n 乘以增量的若干倍,即 n 乘以 logn 的若干倍,但是没人能够构建精确的模型对使用有效的增量序列的希尔排序证明这一点。
那我们为什么还对这个算法感兴趣呢?因为这个算法的思想很简单,而且能获得巨大的性能提升。它相当快,所以在实际中非常有用除了巨大的数组会变得慢,对于中等大小的数组,它甚至可以胜过经典的复杂方法。代码量也不大,通常应用于嵌入式系统,或者硬件排序类的系统,因为实现它只需要很少的代码。
还有就是它引出了很多有趣的问题。这就涉及到了开发算法的智力挑战。如果你觉得我们已经研究了这么长时间的东西很平凡,可以去试着找一个更好的增量序列。尝试一些方法发现一个,并且试着就希尔排序的一般情况的性能得出一些结论。人们已经尝试了50年,并没有获得多少成果。
我们要学到的是我们不需要很多的代码就能开发出很好的算法和实现,而依然有一些等待被发现,也许存在某个增量序列使得希尔排序比其他任何适用于实际序列大小的排序方法都快,我们并不能否认这一点。这就是希尔排序,第一个不平凡的排序方法。
洗牌算法 Shuffling
洗牌与洗牌算法介绍
接下来我们将一起看一个排序的简单应用, 这个应用叫做洗牌.
假设你有一副扑克牌, 你可能会想要做的事之一就是随机地进行摆放卡牌(目标), 这就是洗牌。
我们有一种利用排序来进行洗牌的方法,虽然排序似乎正好与洗牌相反。
这种方法的构想是为一个数组元素产生一个随机实数,然后利用这些随机数作为排序依据。
这是一种很有效的洗牌方法,并且我们可以证明这种方法在输入中没有重复值,并且你在可以产生均匀随机实数的情况下,就能够产生一个均匀的随机排列。如果每种可能的扑克牌排列方式都有相同的出现概率,那就说明这种洗牌方法是正确的。
正确固然好,但这种方法需要进行一次排序,似乎排序对于这个问题来说有些累赘。现在的问题是我们能否做得更好。我们能找到一种更快的洗牌方法吗? 我们真的需要付出进行一次完整排序的代价吗? 这些问题的答案是否定的。
实际上有一种非常简单的方法,可以产生一副均匀随机排列的扑克牌,它只需要线性的时间来完成工作。这种方法的理念是将序数 i 从左到右地遍历数组,i 从 0 到 n 增量。我们从一个已经有序的数组开始洗牌,实际上数组的初始情况并不影响洗牌,每次我们都均匀随机地从 0 和 i 之间挑选一个整数,然后将 a[i] 与这个数代表的元素交换。
- 开始时我们什么也不做,只把第一个元素和它自己交换位置,
- i 变成了2或者说 i 指向了第二张牌,我们随机生成一个 r (在 0 和 i 之间的整数,因为 r 是随机均匀生产的,所以 r 有可能等于 i,i 和 r 的值相同就不用进行交换), 然后我们将这 i 位置和 r 位置的两张牌
- 递增 i 的值,然后生成一个随机整数 r,再交换
一直这样继续进行交换位置。对于每一个 i 的值,我们都正好进行一次交换, 可能有些牌经历了不止一次交换, 但这并不存在问题, 重点是在第
i 张牌左边的牌都是被均匀地洗过去的,在最后我们就会获得一副洗好的扑克牌。
这是一个利用随机性的线性时间洗牌算法,它在很早之前就被证明是正确的,那时甚至电脑实现还未被发明。如果你使用这种方法的话,你会在线性时间内得到一个均匀随机的排列,所以,这绝对是一种简单的洗牌方法。
Java 实现
- 在每次迭代中,随机均匀地选择 0 和 i 之间的整数 r
- 交换 a[i] 和 a[r].
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.StdRandom;
public class Shuffling {
public static void shuffle(int[] a) {
int n = a.length;
for (int i = 0; i < n; i++) {
int r = StdRandom.uniform(i + 1); // [0,i+1) = between 0 and i
int temp = a[i];
a[i] = a[r];
a[r] = temp;
}
}
private static void show(int[] a) {
for (int i = 0; i < a.length; i++) {
StdOut.print(a[i]);
}
}
// simple client
public static void main(String[] args) {
int[] a = {1,2,3,4,5,6,7,8,9};
shuffle(a);
show(a);
}
}
分别进行三次洗牌:
它实现起来也很简单,生成的随机数均匀分布在 0 和 i 之间 (至关重要!)。
你会经常看到程序员们自以为他们实现了一个洗牌应用,实际上他们经常只是为每个数组位置选择了一个随机数组位置与之交换,这种方法实际上并不能实现真正的洗牌。你可以对编号为 i 和 n-1 之间的那些你还没有看到过的牌进行操作,但这种方法并不能洗出一副均匀随机的卡牌。
下面是一个关于软件安全的例子,在软件安全领域有很多难度高并且深层次的问题,但是有一件事是我们可以做的那就是确保我们的算法和宣传中中说的一样好。
这里有一个在线扑克游戏的实现案例在此, 下面就是你可以在网页上找到的洗牌算法案例的代码
Bugs:
- 随机数 r 永远不会等于 52 ⇒ 这意味着最后一张牌会始终在最后一位出现
- 这样洗出的牌不是均匀的 应该在 1 到 i 或者 i+1 和 52 之间随机挑牌交换
- 另一个问题是在这种实现方式中使用一个 32 位数字生成随机数。如果你这么做的话并不能涵盖全部可能的洗牌方式。如果共有52张牌,可能的洗牌方法一共有 52 的阶乘那么多种,这可比 2 的 32 次幂大得多,所以这种方法根本无法产生均匀随机的牌组
- 另一个漏洞则是生成随机数的种子是从午夜到现在这段时间经历的毫秒数,这使得可能的洗牌方式变得更少了。事实上,并不需要多少黑客技巧,一个人就能从 5 张牌中看出系统时钟在干什么。你可以在一个程序里实时计算出所有将来的牌。
(关于这个理解,可以查看edu.princeton.cs.algs4.StdRandom :
private static Random random; // pseudo-random number generator
private static long seed; // pseudo-random number generator seed
// static initializer
static {
// this is how the seed was set in Java 1.4
seed = System.currentTimeMillis();
random = new Random(seed);
}
public static void setSeed(long s) {
seed = s;
random = new Random(seed);
}现在的 jdk 已经不再使用这种方式去定义seed了,正如之前所说的,这会是个bug
)
如果你在做一个在线扑克应用的话 这是一件非常糟糕的事情,因为你肯定希望你的程序洗牌洗得像广告里说的那么好。有许多关于随机数的评论,其中很有名的一句是 "The generation of random numbers is too important to be left to chance -- Robert R. Coveyou" 随机数的生成太过重要。
人们尝试了各种洗牌方法来保证其随机性, 包括使用硬件随机数生成器,或者用很多测试来确认它们的确实是随机的。所以如果你的业务依赖于洗牌, 你最好使用好的随机洗牌代码,洗牌并没有我想象的那么简单,一不小心就会出现很多问题。这是我们的第一个排序应用。
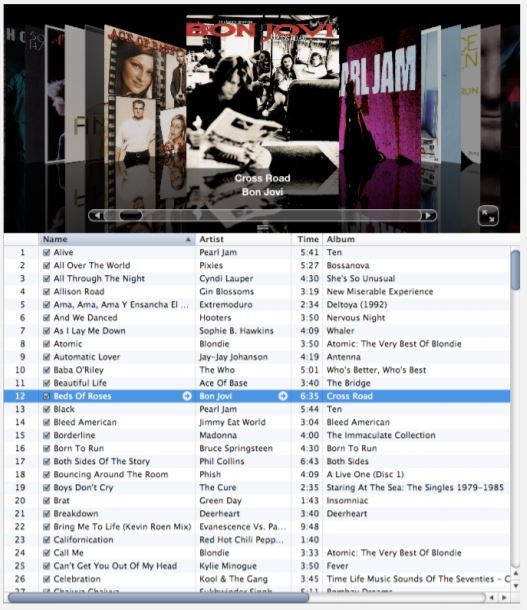
Comparators 比较器
程序员经常需要将数据进行排序,而且很多时候需要定义不同的排序顺序,比如按艺术家的姓名排序音乐库,按歌名排序等。
在Java中,我们可以对任何类型实现我们想要的任何排序算法。Java 提供了两种接口:
- Comparable (java.lang.Comparable)
- Comparator (java.util.Comparator)
使用 Comparable 接口和 compareTo() 方法,我们可以使用字母顺序,字符串长度,反向字母顺序或数字进行排序。 Comparator 接口允许我们以更灵活的方式执行相同操作。
无论我们想做什么,我们只需要知道如何为给定的接口和类型实现正确的排序逻辑。
在文章的最开始我们就谈论过,Java 标准库中会用到排序的类型通过实现 Comparable 接口,也就是这些数据类型实现 compareTo() 方法的实例方法,来实现排序功能。实现此接口的对象列表(和数组)可以通过 Collections.sort(和 Arrays.sort)进行自动排序。
Comparable 接口:回顾
Comparable 接口对实现它的每个类的对象进自然排序,compareTo() 方法被称为它的自然比较方法。所谓自然排序(natural order)就是实现Comparable 接口设定的排序方式。排序时若不指定 Comparator (专用的比较器), 那么就以自然排序的方式来排序。
考虑一个具有一些成员变量,如歌曲名,音乐家名,发行年份的 Musique (法语哈哈哈,同 Music) 类。 假设我们希望根据发行年份对歌曲列表进行排序。 我们可以让 Musique 类实现Comparable 接口,并覆盖 Comparable 接口的 compareTo() 方法。
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/**
* @program: algo
* @description: Exemple to implement Comparable interface for a natural order
* @author: Xiao~
* @create: 2019-03-28 14:35
**/
public class Musique implements Comparable {
private final String song;
private final String artist;
private final int year;
public Musique(String song, String artist, int year) {
this.song = song;
this.artist = artist;
this.year = year;
}
/**
*
* @param musique
* @return natural order by year
* -1 : <
* +1 : >
* 0 : ==
*/
@Override
public int compareTo(Musique musique) {
return this.year - musique.year;
}
@Override
public String toString() {
return "Musique{" +
"song='" + song + '\'' +
", artist='" + artist + '\'' +
", year=" + year +
'}';
}
// simple client
public static void main(String[] args){
List list = new ArrayList<>();
// 暴露歌单系列
list.add(new Musique("You're On My Mind","Tom Misch",2018));
list.add(new Musique("Pumped Up Kicks","Foster The People",2011));
list.add(new Musique("Youth","Troye Sivan",2015));
// 通过 Collections.sort 进行自动排序
Collections.sort(list);
list.forEach(System.out::println);
}
}
运行结果
现在,假设我们想要按照歌手和歌名来排序我们的音乐清单。 当我们使一个集合元素具有可比性时(通过让它实现Comparable接口),我们只有一次机会来实现compareTo()方法。解决方案是使用 Comparator 接口
Comparator 接口
Comparator 接口对实现它的每个类的对象进轮流排序 (alternate order)
实现 Comparator 接口意味着实现 compare() 方法
jdk 8:
public interface Comparator {
int compare(T o1, T o2);
...
} 特性要求:必须是全序关系
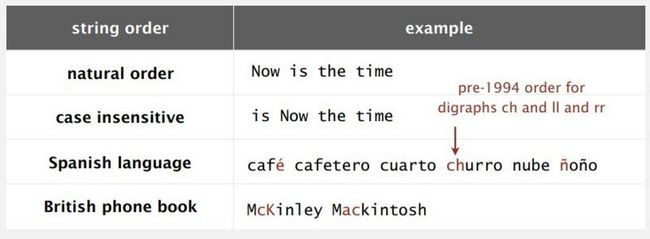
写图中如果前字母相同就会比较后一个字母,以此类推进行排序
与 Comparable 接口不同,Comparable 接口将比较操作(代码)嵌入需要进行比较的类的自身中,而 Comparator 接口则在我们正在比较的元素类型之外进行比较,即在独立的类中实现比较。
我们创建多个单独的类(实现 Comparator)以便由不同的成员进行比较。
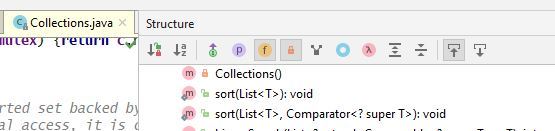
Collections 类有两个 sort() 方法,其中一个 sort() 使用了Comparator,调用 compare() 来排序对象。
Comparator 接口: 系统排序
如果要使用 Java 系统定义的 Comparator 比较器,则:
- 创建 Comparator 对象。
- 将第二个参数传递给Arrays.sort() 或者 Collections.sort()
String[] a;
...
// 这般如此使用的是自然排序
Arrays.sort(a);
...
/**
* 以下这般这般这般都是使用Comparator object定义的轮流排序
**/
Arrays.sort(a, String.CASE_INSENSITIVE_ORDER);
...
Arrays.sort(a, Collator.getInstance(new Locale("es")));
...
Arrays.sort(a, new BritishPhoneBookOrder());
... Comparator 接口: 使用自定义的 sorting libraries
在我们自定义的排序实现中支持 Comparator 比较器:
- 将 Comparator 传递给 sort() 和less(),并在less() 中使用它。
- 使用 Object 而不是 Comparable
请参考:这个Insertion 和 这个InsertionPedantic
import java.util.Comparator;
public class InsertionPedantic {
// 使用的是 Comparable 接口和自然排序
public static > void sort(Key[] a) {
int n = a.length;
for (int i = 1; i < n; i++)
for (int j = i; j > 0 && less(a[j], a[j-1]); j--)
exch(a, j, j-1);
}
// 使用的是 Comparator 接口实现的是客户自定义的排序
public static void sort(Key[] a, Comparator comparator) {
int n = a.length;
for (int i = 1; i < n; i++)
for (int j = i; j > 0 && less(comparator, a[j], a[j-1]); j--)
exch(a, j, j-1);
}
// is v < w ?
private static > boolean less(Key v, Key w) {
return v.compareTo(w) < 0;
}
// is v < w?
private static boolean less(Comparator comparator, Key v, Key w) {
return comparator.compare(v, w) < 0;
}
...
} Comparator 接口: 实现
实现 Comparator :
- 定义一个(嵌套)类实现 Comparator 接口
- 实现 compare() 方法
- 为 Comparator 提供客户端访问权限
下边为我们的音乐列表实现按歌名排序的比较器:
这里我改了一下,把按歌名排序作为自然排序,然后为按歌手和发行年份都创建了两个单独的,嵌入的,实现 Comparator 接口的类
并且提供客户端访问这些内部类
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
/**
* @program: algo
* @description: Exemple to implement Comparable interface for a natural order
* @author: Xiao~
* @create: 2019-03-28 14:35
**/
public class Musique implements Comparable {
public static final Comparator ARTIST_ORDER = new ArtistOrder();
public static final Comparator YEAR_ORDER = new YearOrder();
private final String song;
private final String artist;
private final int year;
public Musique(String song, String artist, int year) {
this.song = song;
this.artist = artist;
this.year = year;
}
/**
* @param musique
* @return natural order: order by song name
*/
@Override
public int compareTo(Musique musique) {
return this.song.compareTo(musique.song);
}
// comparator to music by artist name
private static class ArtistOrder implements Comparator {
@Override
public int compare(Musique o1, Musique o2) {
// Sting class has implemented Comparable interface, we use his native compareTo()
return o1.artist.compareTo(o2.artist);
}
}
// comparator to music by year published
private static class YearOrder implements Comparator {
@Override
public int compare(Musique o1, Musique o2) {
// this trick works here (since no danger of overflow)
return o1.year - o2.year;
}
}
/**
* Returns a comparator for comparing music in lexicographic order by artist name.
*
* @return a {@link Comparator} for comparing music in lexicographic order by artist name
*/
public static Comparator byArtistName() {
return new ArtistOrder();
}
/**
* Returns a comparator for comparing music order by year published.
*
* @return a {@link Comparator} for comparing music by year published.
*/
public static Comparator byYear() {
return new YearOrder();
}
@Override
public String toString() {
return "Musique{" +
"song='" + song + '\'' +
", artist='" + artist + '\'' +
", year=" + year +
'}';
}
// simple client
public static void main(String[] args) {
List list = new ArrayList<>();
list.add(new Musique("You're On My Mind", "Tom Misch", 2018));
list.add(new Musique("Pumped Up Kicks", "Foster The People", 2011));
list.add(new Musique("Youth", "Troye Sivan", 2015));
list.add(new Musique("Royals", "Lorde", 2013));
list.add(new Musique("Atlas", "Coldplay", 2013));
list.add(new Musique("Sugar Roses", "Elsa Kopf", 2013));
Collections.sort(list);
System.out.println("\nOrder by Song name (natural order):");
list.forEach(System.out::println);
System.out.println("\nOrder by artist name:");
Collections.sort(list,Musique.byArtistName());
list.forEach(System.out::println);
System.out.println("\nOrder by year published:");
Collections.sort(list,Musique.byYear());
list.forEach(System.out::println);
}
}
稳定性
典型的应用:
首先,简化下我们的测试客户端:先进行歌手排序; 然后按年份排序。
public static void main(String[] args) {
List list = new ArrayList<>();
list.add(new Musique("You're On My Mind", "Tom Misch", 2018));
list.add(new Musique("Pumped Up Kicks", "Foster The People", 2011));
list.add(new Musique("Youth", "Troye Sivan", 2015));
list.add(new Musique("Royals", "Lorde", 2013));
list.add(new Musique("Atlas", "Coldplay", 2013));
list.add(new Musique("Sugar Roses", "Elsa Kopf", 2013));
System.out.println("\nOrder by artist name:");
Collections.sort(list,Musique.byArtistName());
list.forEach(System.out::println);
System.out.println("\nOrder by year published:");
Collections.sort(list,Musique.byYear());
list.forEach(System.out::println);
} 运行结果:
进行年排序的时候歌手名排序任然保留,排序是稳定的。
一个稳定的排序保留具有相同键值的项的相对顺序。也就是说,一旦你按歌手名排列了之后,接着你想按第二项排列,上边是按照年份,并且对于所有在第二项具有相同键关键字的记录保持按歌手名排列。实际上,不是所有的排列都保留那个性质,这就是所谓的稳定性。
Q. 那插入排序和选择排序,他们都是稳定的排序吗?
A. 插入排序是稳定的,相同的元素在比较的过程不会再互相互换位置,但是选择排序是会的,所以选择排序并不稳定
下边是使用选择排序的运行结果:
首先按名字排序,然后再按 section(第二列) 排序
如图可以看到进行section排序的时候,上一次的按名字排序的顺序不再保留,选择排序并不稳定,shellsort 也不稳定。
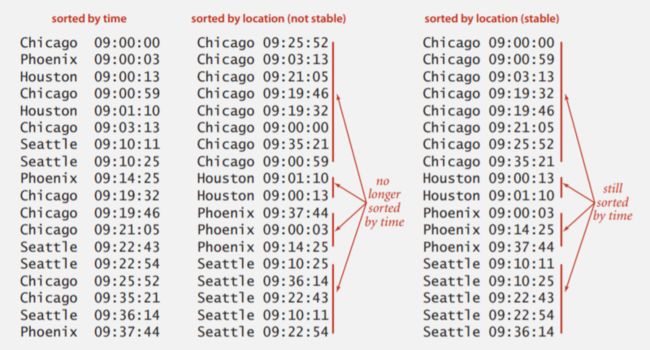
这里有另一个典型的例子,人们想买一场摇滚演唱会的门票,我们有一个按照时间排列的序列,然后将这个序列再按地点排列,我们所希望的是这些按地点排列的序列同时能保持时间顺序 ,如图是一个不稳定的排序,按地点排序完了之后它不会保持按时间的排序,如果他们想用其中一个记录,他们还得重新排列。但如果他们用的是稳定的排序,这些记录还保持着按时间的排序,所以对很多的应用都希望排序算法有稳定性。
值得注意的是,我们在查看代码去判断排序算法是否是稳定的时候要仔细看下比较逻辑使用的是 "<" 还是 "<=".
这些操作是否稳定取决于我们的代码怎么写。在我们的代码中,如果几个个键是相等的,比如我们有如下序列:
- B1 A1 A2 A3 B2 , 其中 A1 = A2 =A3; B1 = B2
我们要保证排序的时候结果是:A1 A2 A3 B1 B2 , 而不会出现:A3 A1 A3 B1 B2 或者其他情况。
在插入排序中,当我们得到 A1,然后排完顺序后,在这种情况下,它数组中就是在起始位置,而当我们得到第二个 A,也就是 A2,只要找到不小于 A2 的记录就停止排列,A1,A2 这俩是相等的,是不小于的,我们就停止排序。所以排序从不越过相同值的记录。如果这里是小于等于,那么它是不稳定的,或者如果我们用另一种方法并据此运行,在代码中让相同值的记录从不越过彼此,那么排序就是稳定的。
具体可以查看插入排序和选择排序的源码。
至今为止我们看到的排序中插入排序是稳定的,后边的归并排序也是稳定的。
Convex hull 凸包
现在我们将通过一个有趣的计算几何领域的例子来了解排序的应用
定义
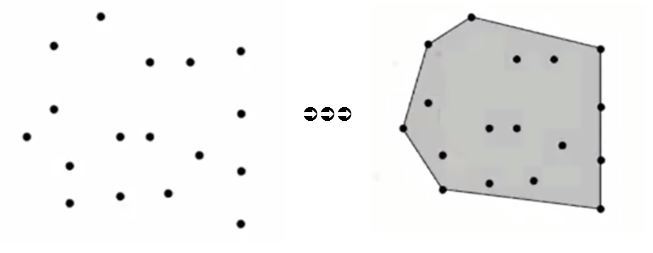
假设现在平面上有一个 n 个点构成的集合, 从几何角度我们可以找到一个“凸包”, 也就是能包含所有点的最小的凸多边形.
由点所构成的集合都有凸包, 凸包还有很多等价的定义方式:
凸包是包含所有点的最小的凸状集合
凸包是最小的能圈起所有点的凸多边形
凸包是最小的包含所有点, 并且顶点也都属于这个集合的凸多边形
我们要做的就是编写一个程序, 对于给定的点集生成它的凸包。
那么这个程序的输出应该是什么呢?我们要用怎样的函数呢?
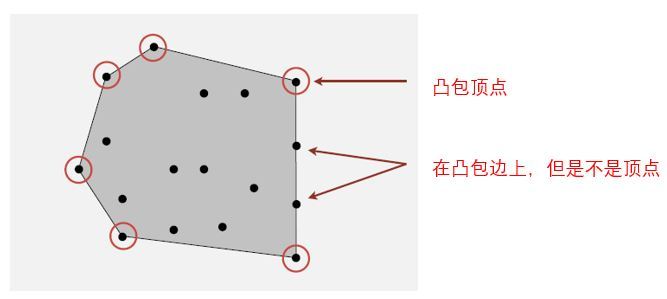
为了这个结果可以更明确易用,这个程序应该输出这个凸包的顶点序列。但是如果集合中的某些点位于凸包的边上,但不是凸包的顶点,那么这些点就不应该被包含在输出序列中。这也例证了计算几何往往是非常困难的。
因为在编程过程中处理这种共线性的情况是很困难的,这门课程将不会耗费很多时间在这个问题上,但是我们必须要能意识到在这类问题中,当我们试着运用一些简单算法时,实际情况可能会变得比预想的复杂很多。
凸包的机械算法:在每个点上扎上图钉,然后用一根带子将所有的钉子围起来收紧,这样我们就得到了这个点集的凸包。
算法链接
我们不会用电脑去编写这样一个程序,但是这表示其实我们可以很好地解决这个问题。
应用
移动规划
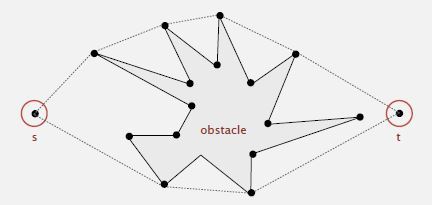
现在我们有一个电脑程序来计算凸包,假设有一个机器人想从s点去t点,但是这中间有一个多边形的障碍物,你想要绕过障碍物抵达t点,最短的路径一定是以下两种情况之一:
s到t的直线,或者是这个点集的凸包的一部分。
相距最远的两点
如果你想找到这个点集中相距最远的两点,有些时候这对于统计计算,或者其他一些应用都是非常重要的。这两个点在凸包上。
如果我们已经知道了这个点集的凸包,那么这个问题就会变得非常简单,因为这两个点就会是凸包上的两个端点。因此我们可以利用凸包的很多几何特性来编写算法。
凸包的特性
这里有两个特性:
- 只能通过逆时针转动来穿过凸包
- 凸包的顶点相对于具有最低 y 坐标的点 p 以极角的递增顺序出现
-
第一,现在你只能用逆时针,或者说是左转的方式来穿过凸包。
- 我们从 p 点到 1 号点,再从 1 号点左转到 5 号点,或者说是逆时针转到 5 号点,然后我们再到 9 号、12号点,最终回到起始点
- 第二,如果你选择在y轴上坐标最小的点,也就是最低点,作为 p 点,那么我们来看一下接下来各点的极角,对比于点 p 的极角,你可以发现 从 x 轴的 p 点指向每个点,这些向量的极角值是递增的,这也是显而易见的事实。
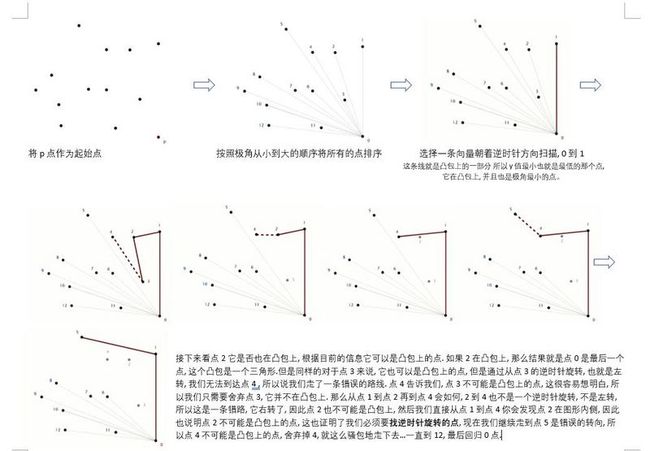
我们将要学习的算法:葛立恒扫描法,就是基于以上这两个事实。
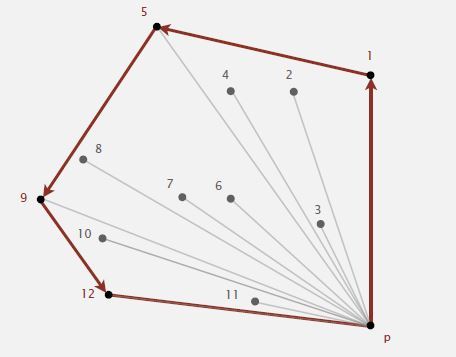
- 我们将p点作为起始点,也就是y轴坐标值最小的点
- 按照以 p (0) 为起点的极角从小到大的顺序,将其它所有的点进行排序 (1-12)
- 然后我们直接舍弃那些无法产生逆时针旋转的点
我们将p点作为起始点, 按照极角从小到大的顺序将所有的点排序, 如果我们选择一条向量, 朝着逆时针方向扫描, 这条向量碰到这些点的顺序是怎样的呢?
然后我们就完成了这个计算过程。通过葛立恒扫描法找到了凸包,在实现这个算法的时候有一些难点,我们不会去细究它们,因为这几节课是讲排序算法的,而不是计算几何学。但是这些说明即使我们有了很好的排序算法,我们也可能需要做一些额外的工作才能在应用中真正地解决问题。
葛立恒扫描法:实现中的挑战
-
我们如何来找到拥有最小y坐标值的点呢?
- 我们可以通过排序(全序排序),我们按照 y 坐标值的大小,将各个点排序(下个内容会涉及)
-
如何根据极角的大小对点进行排序?
- 同样的我们要定义如何比较这些点(通过定义全序排序,下个内容会涉及)
-
如何根据不同的属性对这些点进行排序?
- 葛立恒扫描法是一个完美的例子,我们不仅仅要学会如何排序,和不仅仅要根据定义和比较来排序,还要能对同样的对象进行不同方式的排序。 葛立恒扫描法这个例子可以很好地帮助我们学习这一点,如何判断两点间是否是逆时针旋转,这是几何学的一个小知识点,请查看下方的代码实现
-
我们应该如何更高效地排序呢?
- 我们可以使用希尔排序,但是接下来教程,我们会用经典的排序法,包括归并排序和快速排序。这个例子很好地向我们阐释了高效的排序算法让凸包算法也更高效。这一点对于设计更好的算法是非常重要的原则。一旦我们有了一个好算法,当我们遇到另外一个问题时,我们就可以想一想我们可不可以用它来解决新问题。对于凸包计算,我们有一个好的排序算法就可以得到一个好的凸包算法,因为计算凸包最主要的部分就是排序。
然而在很多现实问题中,因为各种共线问题,实现凸包计算将会面临很多困难。这些在接下来的内容都会涵盖。现在来简短地讲解一下有一个凸包计算的主要部分:
假设平面上有三个点, 点 a、点 b 和点 c, 你需要按照逆时针旋转的方式从点 a 走到点 b 再抵达点 c
在这个例子中我们可以看到只有两个是按照逆时针走的, 其它不是。
我们现在需要一种计算方法来区分这种左转和右转,如果我们不考虑共线的情况,实现这种计算将会很简单。但是如果这些点在同一个直线上,或者斜率是无限大的,我们该如何计算。所以我们要将这种情况也考虑进来,于是我们的编程过程就不像之前想象的那样简单了。我们需要处理共线现象以及浮点数的精确度,但是那些计算几何学的研究者已经解决了这些问题,并且最终的执行代码并没有那么多。
实现 ccw
数学过程
感兴趣可以研究下~~
CCW: 给定三个点:a, b 和 c, a --> b --> c 是否是逆时针方向?
这个计算的基本思想是计算 a 与 b 连线的斜率,和 b 与 c 连线的斜率,比较这两者后,确定转向结果是逆时针,或者是顺时针。
这是详细的数学过程。
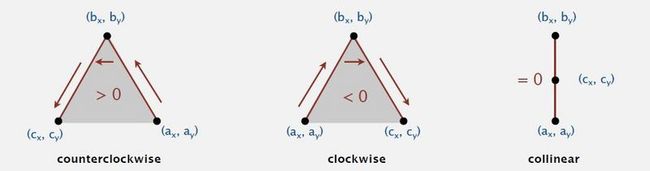
・If signed area > 0, then a → b → c is counterclockwise 逆时针方向.
・If signed area < 0, then a → b → c is clockwise 顺时针方向.
・If signed area = 0, then a → b → c are collinear 共线的.
所以如果我们用平面上的点作为数据来实现这一几何计算,我们可以直接用 ccw() 这个函数计算 (b.x-a.x)(c.y-a.y) - ( b.y-a.y)(c.x-a.x)
public class Point2D
{
private final double x;
private final double y;
public Point2D(double x, double y)
{
this.x = x;
this.y = y;
}
...
public static int ccw(Point2D a, Point2D b, Point2D c)
{
// 这里可能会因为浮点数的四舍五入而引起错误
double area2 = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x);
if (area2 < 0) return -1; // clockwise 顺时针方向
else if (area2 > 0) return +1; // counter-clockwise 逆时针方向
else return 0; // collinear 共线的
}
}然后我们就会看到这里马上可以告诉你这个转弯是逆时针、顺时针还是沿着直线。这部分代码并不多,这个函数是葛立恒扫描法的基本部分。
葛立恒扫描法用两种方式对点进行排序,然后将它们放入栈中。这里将每一个点放进栈,直到遍历所有的点,然后对于用极角排序的栈,我们比较最上面的两个点和第三个点,看看它们的连线是否构成了一个逆时针的转弯。如果不是逆时针 我们就将这个点推出继续寻找下一个点。
可以看到在已有排序算法的情况下我们只需要很少的代码完成凸包算法。
我们有很多现成的排序应用 我们也会用更高效的排序 来写一些新的算法来提高效率。
课后问题
Q. 给定两个数组 a [] 和 b [],每个数组在平面中包含 n 个不同的 2D 点,设计一个复杂度为 ~(n^2) 的算法来计算数组 a [] 和 数组 b [] 中包含的点数
A. 用 shellsort 或者其他复杂度 ~(n^2) 的算法对 2D 点进行排序(先 x 再 y),排序后,同时对每个数组进行扫描(~ n)
Q. 给定两个大小为 n 的整数数组,设计一个复杂度为 ~(n^2) 的算法来确定一个数组是否是另一个数组的置换矩阵。 也就是说,它们是否包含完全相同的元素,只是顺序不同。
A. 对两个数组进行排序然后判断就行
Q.荷兰国旗问题
A.这是一个很经典的关于排序的算法问题,网上也有很多的解释可以查到 (链接 Dutch national flag等更新)
附录
Q. 如果数组已经排好序,那么插入排序比较需要多少次?
A. 平方级
因为选择排序所需要的对比次数与数组是否排好序无关
Q. 如果数组已经是升序排好的,那么插入排序将进行多少次比较?
A. 线性级别
除了第一个元素,其它每个元素都和它左边的元素进行一次比较(除此之外不再有比较),所以 n 个元素,就有 n−1 次比较.
Q. 为什么使用 3x + 1 步长的希尔排序在程序中去构建每次步长时用:while (h < n/3)?
A.
- 这个步长序列值来自于 3x + 1 < N/3 即 h < N/3
可以参考维基百科:Shellsort中关于步长序列列表的 Gap sequences-A003462 已证明的结果 (3^k-1)/2 not greater than [N/3]
更详细的请查看 Sedgewick 教授的证明 :全英+需要一定的数学及数学分析,没有足够的基础,不用深究,这些证明交给数学家或者理论学家就好 - 为什么不用 h = (h - 1)/3,因为 h / 3 是一个整数除法,结果会丢掉余数,也就是说如果 h = 7 则 7 / 3 = 2,与 6 / 3 = 2 是一样的结果