【机器学习笔记33】小波变换
【参考资料】
【1】《小波与傅里叶分析基础》
【2】http://www.pybytes.com/pywavelets/
一、内积空间
内积空间
定义(这里 R n R^n Rn空间和 C n C^n Cn空间是类似的): 一个在复矢量空间V上的内积是一个函数 < . , . > : V × V → C <.,.> : V \times V \to C <.,.>:V×V→C,它满足如下性质:
- 正性: ⟨ v , v ⟩ > 0 \langle v,v \rangle > 0 ⟨v,v⟩>0,对于任意非零的 v ∈ V v \in V v∈V
- 共轭对称性: ⟨ w , v ⟩ ‾ = ⟨ v , w ⟩ \overline{\langle w,v \rangle} = \langle v,w \rangle ⟨w,v⟩=⟨v,w⟩,对于所有的 v , w ∈ V v, w \in V v,w∈V
- 均匀性: ⟨ c v , w ⟩ = c ⟨ v , w ⟩ \langle cv,w \rangle = c\langle v,w \rangle ⟨cv,w⟩=c⟨v,w⟩,这里对于所有的 v , w ∈ V v, w \in V v,w∈V, c ∈ C c \in C c∈C属于比例因子
- 加性: ⟨ u + v , w ⟩ = ⟨ u , w ⟩ + ⟨ v , w ⟩ \langle u + v,w \rangle = \langle u,w \rangle + \langle v,w \rangle ⟨u+v,w⟩=⟨u,w⟩+⟨v,w⟩,这里对于所有的 u , v , w ∈ V u, v, w \in V u,v,w∈V
L 2 L^2 L2空间和 l 2 l^2 l2空间
定义: 对于 a ≤ t ≤ b a \le t \le b a≤t≤b,空间 L 2 ( [ a , b ] ) L^2([a, b]) L2([a,b])表示所有的平方可积函数所组成的空间,即:
L 2 ( [ a , b ] ) = { f : [ a , b ] → C ; ∫ a b ∣ f ( t ) ∣ 2 d t < ∞ } L^2([a, b]) = \{f:[a, b] \to C; \int_a^b|f(t)|^2dt < \infty \} L2([a,b])={f:[a,b]→C;∫ab∣f(t)∣2dt<∞}
定义: l 2 l^2 l2空间是由所有序列 . . . , x − 1 , x 0 , x 1 , . . . . ..., x_{-1}, x_0, x_1, .... ...,x−1,x0,x1,....,其中 x i ∈ C x_i \in C xi∈C且 ∑ − ∞ + ∞ ∣ x n ∣ 2 < ∞ \sum\limits_{-\infty}^{+\infty}|x_n|^2 < \infty −∞∑+∞∣xn∣2<∞。该空间的内积定义为 ∑ − ∞ + ∞ x n y n ˉ \sum\limits_{-\infty}^{+\infty} x_n \bar{y_n} −∞∑+∞xnynˉ
备注:对于信号系统而言,其物理意义表示为信号的能量有限
正交
设V是内积空间,则有下面三类正交
- V中的两个矢量X和Y,若 ⟨ X , Y ⟩ = 0 \langle X, Y \rangle = 0 ⟨X,Y⟩=0,则称X和Y正交
- 矢量集 e i , i = 1 , . . . , N e_i, i = 1, ..., N ei,i=1,...,N称为正交,对于每一个 e i e_i ei具有单位长度 ∥ e i ∥ = 1 \Vert e_i \Vert = 1 ∥ei∥=1,并且彼此正交,即 i ≠ j i \ne j i̸=j时 e j e_j ej与 e i e_i ei正交
- 两个子空间 V 1 V 2 ⊂ V V1 \quad V2 \subset V V1V2⊂V称为正交,是指 V 1 V_1 V1中的每个矢量同 V 2 V_2 V2中的每个矢量正交
正交基是指空间V的一个矢量基,它是正交的。
举例:
函数f(t)=sint和g(t)=cost在 L 2 ( [ − π , π ] ) L^2([-\pi, \pi]) L2([−π,π])上正交,因为:
⟨ f , g ⟩ = ∫ − π π sin ( t ) cos ( t ) d t \langle f, g \rangle = \int\limits_{-\pi}^{\pi} \sin (t) \cos (t) dt ⟨f,g⟩=−π∫πsin(t)cos(t)dt
= 1 2 ∫ − π π sin ( 2 t ) d t = 0 =\dfrac{1}{2} \int\limits_{-\pi}^{\pi} \sin (2t) dt = 0 =21−π∫πsin(2t)dt=0
正交投影
假设 V 0 V_0 V0是内积空间V的一个有限维子空间。对于任意 v ∈ V v \in V v∈V,v在 V 0 V_0 V0上的正交投影是唯一的矢量 v 0 ∈ V 0 v_0 \in V_0 v0∈V0,它最接近v。或者说 v − v 0 v - v_0 v−v0这个矢量与 V 0 V_0 V0正交。
正交补定义: 设 V 0 V_0 V0是内积空间V的空间, V 0 V_0 V0的正交补,记作 V 0 ⊥ V_0^{\perp} V0⊥,是V上所有与 V 0 V_0 V0正交的矢量的集合: V 0 ⊥ = { v ∈ V ; ⟨ v , w ⟩ = 0 , w ∈ V 0 } V_0^{\perp} = \{ v \in V; \langle v, w \rangle = 0, w \in V_0 \} V0⊥={v∈V;⟨v,w⟩=0,w∈V0}
对于上面图中二维的例子,向量 v − v 0 v - v_0 v−v0就是 v 0 v_0 v0的正交补,而两者的直和就是v。详见定理如下:
设 V 0 V_0 V0是内积空间V的有限维子空间。对于每个矢量 v ∈ V v \in V v∈V,可以唯一地表示为 v = v 0 + v 1 v = v_0 + v_1 v=v0+v1,其中 v 0 ∈ V 0 v_0 \in V_0 v0∈V0而 v 1 ∈ V 0 ⊥ v_1 \in V_0^{\perp} v1∈V0⊥;即 V = V 0 ⊕ V 0 ⊥ V = V_0 \oplus V_0^{\perp} V=V0⊕V0⊥
备注:这部分是小波分析在整个泛函知识领域里最重要的一点,是小波分析的基础!!
二、Haar小波分析
Haar尺度函数(父小波)
Haar尺度函数定义如下:
ϕ ( x ) = { 1 , 0 ≤ x < 1 0 , o t h e r \phi(x) = \begin{cases} 1, & 0 \le x < 1 \\ 0, & other \end{cases} ϕ(x)={1,0,0≤x<1other
令 V 0 V_0 V0是 ∑ k ∈ Z a k ϕ ( x − k ) \sum\limits_{k \in Z} a_k \phi(x - k) k∈Z∑akϕ(x−k)函数所组成的空间,则 V 0 V_0 V0所显示的函数图形如下:

同时我们有更细粒度的 V 1 V_1 V1是 ∑ k ∈ Z a k ϕ ( 2 x − k ) \sum\limits_{k \in Z} a_k \phi(2x - k) k∈Z∑akϕ(2x−k)函数所组成的空间,以及更进一步的 V j V_j Vj。
上述空间具备了包含关系 V 0 ⊃ V 1 ⊃ V 2 , . . . , V j − 1 ⊃ V j V_0 \supset V_1 \supset V_2, ..., V_{j-1} \supset V_j V0⊃V1⊃V2,...,Vj−1⊃Vj
同时由于:
- ∥ ϕ ( x − k ) ∥ 2 = ∫ − ∞ + ∞ ϕ ( x − k ) 2 d x = 1 \Vert \phi(x - k) \Vert ^ 2 = \int_{-\infty}^{+\infty} \phi(x - k)^2 dx = 1 ∥ϕ(x−k)∥2=∫−∞+∞ϕ(x−k)2dx=1
- ⟨ ϕ ( x − j ) , ϕ ( x − k ) ⟩ = ∫ − ∞ + ∞ ϕ ( x − k ) ϕ ( x − j ) d x = 0 \langle \phi(x - j), \phi(x - k)\rangle = \int_{-\infty}^{+\infty} \phi(x - k) \phi(x - j) dx = 0 ⟨ϕ(x−j),ϕ(x−k)⟩=∫−∞+∞ϕ(x−k)ϕ(x−j)dx=0
(重要)可知 ϕ ( x − k ) \phi(x - k) ϕ(x−k)是空间 V 0 V_0 V0的一组正交基,同理可知 2 j / 2 ϕ ( 2 j x − k ) 2^{j/2}\phi(2^j x - k) 2j/2ϕ(2jx−k)是 V j V_j Vj的一组正交基
Haar小波函数(母小波)
Haar小波函数即其尺度函数的正交补。例如:
ψ ( x ) = ϕ ( 2 x ) − ϕ ( 2 x − 1 ) \psi(x) = \phi(2x) - \phi(2x - 1) ψ(x)=ϕ(2x)−ϕ(2x−1),有 ∫ − ∞ + ∞ ϕ ( x ) ψ ( x ) d x = 0 \int\limits_{-\infty}^{+\infty}\phi(x)\psi(x)dx =0 −∞∫+∞ϕ(x)ψ(x)dx=0
定理: 令 W j W_j Wj是由形如
∑ k ∈ Z a k ψ ( 2 j x − k ) a k ∈ R \sum\limits_{k \in Z} a_k \psi(2^j x - k) \quad a_k \in R k∈Z∑akψ(2jx−k)ak∈R的函数所组成的空间。 W j W_j Wj是 V j V_j Vj的正交补,即 V j + 1 = V j ⊕ W j V_{j+1} = V_j \oplus W_j Vj+1=Vj⊕Wj
Haar小波的分解与重构
所谓的小波分解就是把 L 2 ( R ) L^2(R) L2(R)分解成其子空间的直积和: L 2 ( R ) = V 0 ⊕ W 0 ⊕ W 1 . . . . L^2(R)=V_0 \oplus W_0 \oplus W_1 .... L2(R)=V0⊕W0⊕W1....。也就是说对于特别的 f ∈ L 2 ( R ) f \in L^2(R) f∈L2(R)我们有 f = f 0 + ∑ j = 0 ∞ w j f = f_0 + \sum\limits_{j=0}^{\infty}w_j f=f0+j=0∑∞wj。
小波信号处理的流程如下:
第一步取样:对于连续信号y=f(t)取适当的J进行采样,令 a k J = f ( k / 2 J ) a_k^J = f(k/2^J) akJ=f(k/2J),存在f(t)的一个近似 f J ( t ) = ∑ k ∈ Z a k J ϕ ( 2 J x − k ) f_J(t) = \sum\limits_{k \in Z}a_k^J \phi(2^J x - k) fJ(t)=k∈Z∑akJϕ(2Jx−k)
第二步分解:由上述知识可知 f J = W j − 1 + W j − 2 + . . . + W 0 + f 0 f_J = W_{j-1} + W_{j-2} + ... + W_0 + f_0 fJ=Wj−1+Wj−2+...+W0+f0,即
f J ( x ) = ∑ j = 0 J − 1 w j + f 0 f_J(x) = \sum\limits_{j=0}^{J-1}w_j + f_0 fJ(x)=j=0∑J−1wj+f0
= ∑ j = 0 J − 1 ( ∑ k ∈ Z b l j ψ ( 2 j x − k ) ) + ∑ k ∈ Z a k 0 ϕ ( x − k ) =\sum\limits_{j=0}^{J-1}(\sum_{k \in Z}b_l^j \psi(2^jx -k)) + \sum_{k \in Z}a_k^0 \phi(x - k) =j=0∑J−1(∑k∈Zbljψ(2jx−k))+∑k∈Zak0ϕ(x−k)
第三步处理:修改小波系数 b k j b_k^j bkj进行信号处理,若处理高频滤波,则将大于某一阈值的 b k j b_k^j bkj置零;若是压缩数据,则将小于某一阈值的 b k j b_k^j bkj置零。
第四步重构:利用修改后的小波系数重构
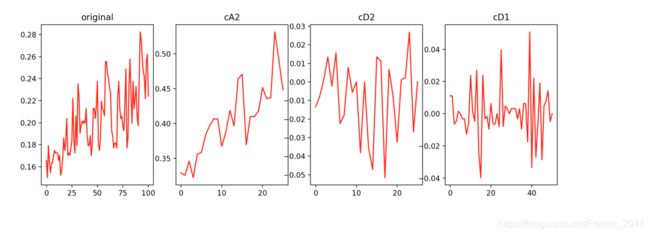
三、程序实现(基于pyWavelet)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pywt import wavedec
df = pd.read_csv('./data/test.csv', sep=',')
data = df['std_value'].astype(float)
coeffs= wavedec(data, 'haar', level=2)
titles = ["original","cA2","cD2","cD1"]
cA2, cD2, cD1 = coeffs
fig = plt.figure(figsize=(14, 4))
for i, a in enumerate([data, cA2, cD2, cD1]):
ax = fig.add_subplot(1, 4, i + 1)
plt.plot(a,'r')
ax.set_title(titles[i], fontsize=12)
plt.show()