HMM算例 python 有代码
原理
原理文字来源于
https://www.cnblogs.com/lcj1105/p/4936103.html
隐马尔可夫(HMM)。
还是用最经典的例子,掷骰子。假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子(称这个骰子为D6),6个面,每个面(1,2,3,4,5,6)出现的概率是1/6。第二个骰子是个四面体(称这个骰子为D4),每个面(1,2,3,4)出现的概率是1/4。第三个骰子有八个面(称这个骰子为D8),每个面(1,2,3,4,5,6,7,8)出现的概率是1/8。
假设我们开始掷骰子,我们先从三个骰子里挑一个,挑到每一个骰子的概率都是1/3。然后我们掷骰子,得到一个数字,1,2,3,4,5,6,7,8中的一个。不停的重复上述过程,我们会得到一串数字,每个数字都是1,2,3,4,5,6,7,8中的一个。例如我们可能得到这么一串数字(掷骰子10次):1 6 3 5 2 7 3 5 2 4
这串数字叫做可见状态链。但是在隐马尔可夫模型中,我们不仅仅有这么一串可见状态链,还有一串隐含状态链。在这个例子里,这串隐含状态链就是你用的骰子的序列。比如,隐含状态链有可能是:D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
一般来说,HMM中说到的马尔可夫链其实是指隐含状态链,因为隐含状态(骰子)之间存在转换概率(transition probability)。在我们这个例子里,D6的下一个状态是D4,D6,D8的概率都是1/3。D4,D8的下一个状态是D4,D6,D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚,但是我们其实是可以随意设定转换概率的。比如,我们可以这样定义,D6后面不能接D4,D6后面是D6的概率是0.9,是D8的概率是0.1。这样就是一个新的HMM。
同样的,尽管可见状态之间没有转换概率,但是隐含状态和可见状态之间有一个概率叫做输出概率(emission probability)。就我们的例子来说,六面骰(D6)产生1的输出概率是1/6。产生2,3,4,5,6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如,我有一个被赌场动过手脚的六面骰子,掷出来是1的概率更大,是1/2,掷出来是2,3,4,5,6的概率是1/10。
其实对于HMM来说,如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率,做模拟是相当容易的。但是应用HMM模型时候呢,往往是缺失了一部分信息的,有时候你知道骰子有几种,每种骰子是什么,但是不知道掷出来的骰子序列;有时候你只是看到了很多次掷骰子的结果,剩下的什么都不知道。如果应用算法去估计这些缺失的信息,就成了一个很重要的问题。这些算法我会在下面详细讲。
算例实现
代码是自己的啦
拿股票数据进行演示
读取数据
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu
# @Date : 2020/5/31
import datetime
import numpy as np
import pandas as pd
from hmmlearn.hmm import GaussianHMM
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
Stocks=pd.read_csv('data/TSLA_data.csv')
print(Stocks.head())
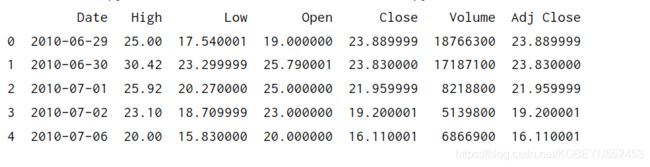
输入因素有 日期,最高价,最低价,开盘价,收盘价,成交量,资金净额
删除我们不想要的因素
Stocks.reset_index(inplace=True,drop=False)
Stocks.drop(['Open','High','Low','Adj Close'],axis=1,inplace=True)
#剩下Date Close收盘价23.889999 Volume成交量8218800
Stocks['Date'] =pd.to_datetime(Stocks['Date'])
Stocks['Date'] = Stocks['Date'].apply(datetime.datetime.toordinal)
Stocks = list(Stocks.itertuples(index=False, name=None))
print(Stocks)
dates = np.array([q[0] for q in Stocks], dtype=int)
end_val = np.array([q[1] for q in Stocks])#(2079,)#收盘价
volume = np.array([q[2] for q in Stocks])[1:]#(2078,)#成交量
diff = np.diff(end_val)#前后收盘价 价格差值
dates = dates[1:]
end_val = end_val[1:]
X = np.column_stack([diff, end_val,volume])#收盘价差值,收盘价 ,成交量
print(X)
建模
model = GaussianHMM(n_components=4, covariance_type="full", n_iter=1000,random_state=1)
model.fit(X)
logprob, hidden_states = model.decode(X, algorithm="viterbi")
#random_state 是每次输出结果一样,
对新的数据进行预测,可以采用hidden_states = model.predict(X),或者hidden_states = model.predict(X)
#其中 model.predict(X) 返回只有标签,而 model.decode(X, algorithm=“viterbi”),返回有:所生成状态序列的对数概率logprob,和依据algorithm加密器获得的X中每个样本的标签hidden_states
结果可视化
对成交量进行结果可视化
hidden_states=pd.DataFrame(hidden_states)#输出状态
end_val=pd.DataFrame(end_val)#收盘价
volume=pd.DataFrame(volume)#成交量
c=pd.concat([hidden_states,volume],axis=1)
for i in range(len(c)):
if c.iloc[i,0]==0:
plt.scatter(i,c.iloc[i,1], c='b')
elif c.iloc[i,0]==1:
plt.scatter(i,c.iloc[i,1], c='r')
elif c.iloc[i, 0] == 2:
plt.scatter(i,c.iloc[i, 1], c='c')
else:
plt.scatter(i,c.iloc[i,1])
plt.show()

HMM模型只是能分离出不同的状态,具体每个状态对应现实的市场意义,需要人为观察。
GaussianHMM是针对连续性输入有作用的。
离散值的用MultinomialHMM
#本文的算例是非监督学习,后续有时间研究监督学习的hmm。
在HMM中,如果已知观察序列和产生观察序列的状态序列,那么可用以下哪种方法直接进行参数估计()
A.EM算法
B.维特比算法
C.前向后向算法
D.极大似然估计
EM算法: 只有观测序列,无状态序列时来学习模型参数,即Baum-Welch算法
维特比算法: 用动态规划解决HMM的预测问题,不是参数估计
前向后向:用来算概率
极大似然估计:即观测序列和相应的状态序列都存在时的监督学习算法,用来估计参数