Kaldi thchs30手札（七） DNN-HMM模型的训练

欢迎大家关注我的博客 http://pelhans.com/ ，所有文章都会第一时间发布在那里~

本部分是对Kaldi thchs30 中run.sh的代码的line 106-107 行研究和知识总结，主要内容为Kaldi中nnet1的DNN-HMM模型训练。

概览

首先放代码：

#train dnn model                                         
local/nnet/run_dnn.sh --stage 0 --nj $n  exp/tri4b exp/tri4b_ali exp/tri4b_ali_cv || exit 1;

只有一行代码，目标是采用DNN来训练一个声学模型，至于HMM部分则与GMM-HMM的HMM相似。下面对DNN部分和DNN-HMM框架进行详细介绍.

DNN-HMM模型

之前的语音识别框架都是基于GMM-HMM的，然而浅层的模型结构的建模能力有限，不能捕捉获取数据特征之间的高阶相关性。而DNN-HMM系统利用DNN很强的表现学习能力，再配合HMM的系列化建模能力，在很多大规模语音识别任务中都超过了GMM模型。

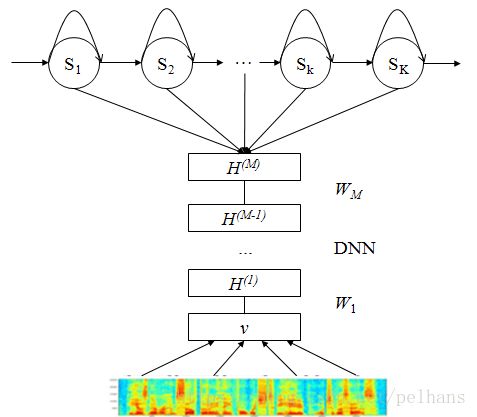
下图给出一个DNN-HMM系统的结构图。在这个框架中，HMM用来描述语音信号的动态变化，用DNN的每个输出节点来估计连续密度HMM的某个状态的后验概率。在Kaldi thchs30中，该模型的整体输入是fbank特征，而后DNN对所有聚类后的状态(如状态绑定后的三音素)的似然度进行建模，得到后验概率。再结合HMM对其进行解码。

DNN的建模对象

我们知道，语音识别问题可表示为找到使得概率 P(W|O) P ( W | O ) 最大的句子：

W===argmaxWP(W|O)argmaxWp(O|W)P(W)/P(W)argmaxWp(O|W)P(W) W = arg ⁡ max W P ( W | O ) = arg ⁡ max W p ( O | W ) P ( W ) / P ( W ) = arg ⁡ max W p ( O | W ) P ( W )

其中p(w)是语言模型， p(o|w) p ( o | w ) 就是声学模型。用Viterbi解码的方式对其进行展开:

p(o|w)=≈∑qp(o,q|w)p(q|w)maxπ(q0)∏t=1Taqt−1qt∏t=1Tp(ot|qt) p ( o | w ) = ∑ q p ( o , q | w ) p ( q | w ) ≈ max π ( q 0 ) ∏ t = 1 T a q t − 1 q t ∏ t = 1 T p ( o t | q t )

传统的GMM-HMM模型中，我们使用GMM对声学模型进行建模，它是一个生成模型，可以直接生成似然概率
p(ot|qt) p ( o t | q t ) ，这个似然概率就是HMM所需要的观察概率。

而现在我们要使用DNN，但DNN只能给出观测值输入到DNN输出层之后在每个节点(状态)上的后验概率
p(qt|ot) p ( q t | o t ) ，因此我们通过贝叶斯定理将其转换一下：

p(ot|qt)=p(qt|ot)p(ot)/p(qt) p ( o t | q t ) = p ( q t | o t ) p ( o t ) / p ( q t )

其中 p(ot) p ( o t ) 不变， p(qt) p ( q t ) 是关于状态的先验概率，这个概率也是训练过程中训练出来的(就是把观测值(特征向量)网状态上对齐，跟某个状态对齐的观测值的个数占比就是这个状态的先验概率)。这样我们就可以对DNN-HMM模型进行解码和训练了。

基于DNN-HMM的模型训练算法

DNN-HMM 模型的主要训练步骤如下:

1. 首先训练一个状态共享的三音素 GMM-HMM 汉语识别系统,使用决策树来决定如何共享状态。设训练完成的系统为 gmm-hmm。

2. 用步骤 1 得到的 gmm-hmm 初始化一个新隐马尔可夫模型(包括转移概率,观测概率,隐马尔可夫模型的状态),并生成一个 DNN-HMM 模型,设该模型为 dnn-hmm1。

3. 预训练 dnn-hmm1 系统中的深度神经网络,得到的深度神经网络为ptdnn。

4. 使用 gmm-hmm 系统对语音训练数据作排列(即求出训练数据对应哪个隐马尔可夫模型中的状态),得到的数据设为 align-raw。

5. 使用步骤 4 得到的数据对 ptdnn的参数作微调(可以使用随机梯度下降算法)。设得到的深度神经网络为 dnn。

6. 利用 dnn 与 dnn-hmm1 和最大似然算法重新估计隐马尔可夫中的参数(转移概率,观测概率),设新得到的系统为 dnn-hmm2。

7. 如果步骤 6 的精度不再提高则退出算法,否则使用 dnn 和 dnn-hmm2产生新的语音训练数据的排列数据,然后回到步骤 5。

8. 利用训练数据估计概率 P(qt) P ( q t ) 的值。

Kaldi中的DNN

Kaldi中的DNN实现有三个版本，其中Karel的nnet1支持单GPU训练，好处是实现简单，便于修改。另两个版本的作者是Dan的nnet2和nnet3，其中nnet2支持多GPU训练，它是在nnet1的基础上扩展重写而成的。nnet3是nnet2的新版。thchs30使用的是nnet1和nnet3.这里先对nnet1进行介绍。

由于此部分在Kaldi官网有详尽的介绍，因此此处我只把其实现的大体流程整理一下。

训练流程

脚本 egs/wsj/s5/local/nnet/run_dnn.sh分下面这些步骤：

1. 存储在本地的40维fMLLR特征, 使用steps/nnet/make_fmllr_feats.sh,这简化了训练脚本，40维的特征是使用CMN的MFCC-LDA-MLLT-fMLLR。

2. RBM 预训练, steps/nnet/pretrain_dbn.sh,是根据Geoff Hinton’s tutorial paper来实现的。训练方法是使用1步马尔科夫链蒙特卡罗采样的对比散度算法(CD-1)。 第一层的RBM是Gaussian-Bernoulli， 和接下里的RBMs是Bernoulli-Bernoulli。这里的超参数基准是在100h Switchboard subset数据集上调参得到的。如果数据集很小的话，迭代次数N就需要变为100h/set_size。训练是无监督的，所以可以提供足够多的输入特征数据目录。
   当训练Gaussian-Bernoulli的RBM时，将有很大的风险面临权重爆炸，尤其是在很大的学习率和成千上万的隐层神经元上。为了避免权重爆炸，我们在实现时需要在一个minbatch上比较训练数据的方差和重构数据的方差。如果重构的方差是训练数据的2倍以上，权重将缩小和学习率将暂时减小。

3. 帧交叉熵训练，steps/nnet/train.sh, 这个阶段时训练一个DNN来把帧分到对应的三音素状态(比如： PDFs)中。这是通过mini-batch随机梯度下降法来做的。默认的是使用Sigmoid隐层单元，Softmax输出单元和全连接层AffineTransform。学习率是0.008，minibatch的大小是256；我们未使用冲量和正则化(注: 最佳的学习率与不同的隐含层单元类型有关，sigmoid的值0.008,tanh是0.00001)。
   输入变换和预训练DBN(比如：深度信念网络,RBMs块)是使用选项
   ‘–input-transform’和’–dbn’传递给脚本的，这里仅仅输出层是随机初始化的。我们使用提早停止(early stopping)来防止过拟合。为了这个，我们需要在交叉验证集(比如: held-out set)上计算代价函数，因此两对特征对齐目录需要做有监督的训练。

4. sMBR(State-level minimum Bayes risk)序列区分性训练，steps/nnet/train_mpe.sh(minimum phone erro, MPE), 这个阶段对所有的句子联合优化来训练神经网络，比帧层训练更接近一般的ASR目标。

   • sMBR的目标是最大化从参考的对齐中得到的状态标签的期望正确率，然而一个词图框架是来使用表示这种竞争假设。
   • 训练是使用每句迭代的随机梯度下降法，我们还使用一个低的固定的学习率1e-5 (sigmoids)和跑3-5轮。
   • 当在第一轮迭后重新生成词图，我们观察到快速收敛。我们支持MMI, BMMI, MPE 和sMBR训练。所有的技术在Switchboard 100h集上是相同的，仅仅在sMBR好一点点。
   • 在sMBR优化中，我们在计算近似正确率的时候忽略了静音帧。具体更加详细的描述见http://www.danielpovey.com/files/2013_interspeech_dnn.pdf

个人补充

限制玻尔兹曼机(RBM)

玻尔兹曼机(Boltzmann Machines, BM)

玻尔兹曼机是二值的马尔科夫随机场(Markov Random Filed)，一个玻尔兹曼机可以表示为带权重的无向图：

如上图所示，对于有n个节点的无向图，由于每个节点是二值的，所以一共有 2n 2 n 个状态，对于一个节点 xi x i ，其值为1 的时候表示这个节点是’on’，其值为1的时候表示这个节点是’off’，对于一个状态向量 x x ,也就是长度为n的向量，表示这个图n个节点的状态，其能量值为:

E(x)=−bTx−xTWx=−∑j=1nbjxj−∑i,jxiWi,jxj E ( x ) = − b T x − x T W x = − ∑ j = 1 n b j x j − ∑ i , j x i W i , j x j

x的概率分布为：

P(x)=1Zexp(−E(x)) P ( x ) = 1 Z exp ⁡ ( − E ( x ) )

Z=∑x′exp(−E(x′)) Z = ∑ x ′ exp ⁡ ( − E ( x ′ ) )

其中b表示长度为n的偏置向量，W是两节点间的连接权值矩阵。

典型的BM有可见节点(Visible Node)和隐含节点(Hidden Node)， 可见节点后面使用v表示,隐含节点用h表示.在这里我们可以把v理解为我们可见的训练参数，h理解为我们在训练数据里面的一些未知隐变量，如LDA里面的隐藏话题,现在的问题是，给定一组可见节点的训练数据 v1,v2,…,vn v 1 , v 2 , … , v n ，现在的问题是，寻找参数W和b使得训练语料的最大似然函数最大：

W∗.b∗=argmaxW,blD(W,b) W ∗ . b ∗ = arg ⁡ max W , b l D ( W , b )

lD(W,b)=∏i=1nP(vi) l D ( W , b ) = ∏ i = 1 n P ( v i )

P(v)=∑h′P(v⊙h′)=∑h′exp(−E(v⊙h′))∑h′v′exp(−E(v⊙h′)) P ( v ) = ∑ h ′ P ( v ⊙ h ′ ) = ∑ h ′ exp ⁡ ( − E ( v ⊙ h ′ ) ) ∑ h ′ v ′ exp ⁡ ( − E ( v ⊙ h ′ ) )

理论上给出似然函数后，我们可以通过对其求对数而后对参数进行求导得到，但在实际操作中由于巨大的计算量变得不可接受。因此常常使用MCMC和Gibbs采样方法。

限制玻尔兹曼机（Restricted Boltzmann Machines, RBM）

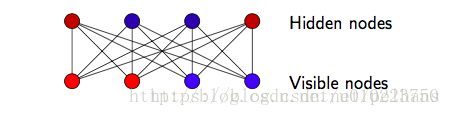
限制玻尔兹曼机是一种特殊的玻尔兹曼机，之所以是受限的，是因为，在RBM中，所有的连接都是在隐含节点和可见节点之间的，而在隐含节点内部和可见节点内部并没有连接,一个典型的RBM的结构就是一个二分图：

此时RBM的能量函数和之前的BM是一样的。

RBM在DNN-HMM模型中的作用

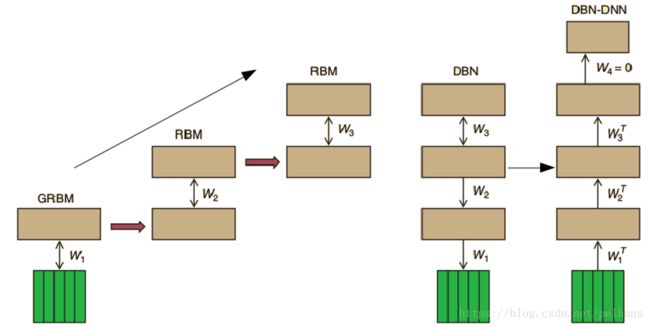
在wsj的run_dnn.sh里采用了RBM训练步骤。通过RBM所得到的网络参数权重将会用来初始化最终的深度学习结构的参数。之后我们就可以使用有标注的数据并利用监督学习的方法来微调整个网络。**使用该方法能有效训练具有多层隐藏层的深度神经网络,特别是能够有效改变最初几层网络的权重。由于使用了大量的无标签数据,在一定程度上避免了优化过程中局部最小值的影响,可以得到更优化的模型。RBM在DNN-HMM中的应用流程为：

对比散度（Contrastive Divergence，CD)

在求解的过程中，我们使用了Gibbs采样对P(v)抽样出来一大堆小v,然后再蒙特卡洛求均值求解。但问题是Gibbs采样需要一直转移到1000次再抽样才能站的按照p(x)概率分布进行，太慢了，因此就不使用个1000次转移之后，我们直接从训练集 S=v1,v2,…,vn S = v 1 , v 2 , … , v n 这个v作为出发点(原来直接是随机的出发点)，转移k次就够了，而不用等转移1000次之后。

经过这种方案得到的梯度会以差值的形式展现。具体的数学推到详见受限玻尔兹曼机（RBM）学习笔记（六）对比散度算法

参考

GMM-HMM和DNN-HMM 框架图如何理解

Context-Dependent Pre-Trained Deep Neural Networks for Large-Vocabulary Speech Recognition

Deep Neural Networks in Kaldi

Karel’s DNN implementation

kaldi中的深度神经网络

受限制玻尔兹曼机RBM原理简介