【PyTorch】50行代码实现GAN——PyTorch
本文来源于PyTorch中文网。
一直想了解GAN到底是个什么东西,却一直没能腾出时间来认真研究,前几日正好搜到一篇关于PyTorch实现GAN训练的文章,特将学习记录如下,本文主要包含两个部分:GAN原理介绍和技术层面实现。
一、什么是GAN
2014 年,Ian Goodfellow 和他在蒙特利尔大学的同事发表了一篇震撼学界的论文。没错,我说的就是《Generative Adversarial Nets》,这标志着生成对抗网络(GAN)的诞生,而这是通过对计算图和博弈论的创新性结合。他们的研究展示,给定充分的建模能力,两个博弈模型能够通过简单的反向传播(backpropagation)来协同训练。
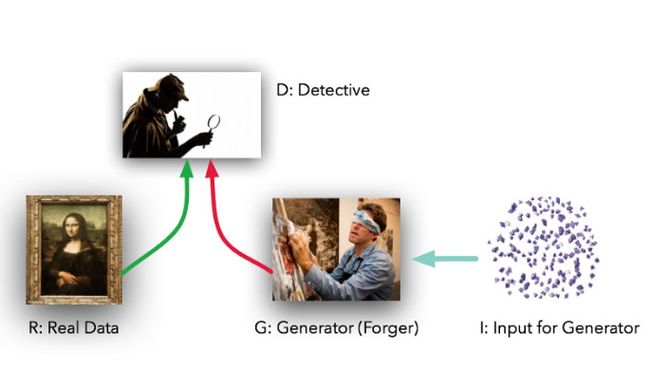
这两个模型的角色定位十分鲜明。给定真实数据集 R,G 是生成器(generator),它的任务是生成能以假乱真的假数据;而 D 是判别器 (discriminator),它从真实数据集或者 G 那里获取数据, 然后做出判别真假的标记。Ian Goodfellow 的比喻是,G 就像一个赝品作坊,想要让做出来的东西尽可能接近真品,蒙混过关。而 D 就是文物鉴定专家,要能区分出真品和高仿(但在这个例子中,造假者 G 看不到原始数据,而只有 D 的鉴定结果——前者是在盲干)。
理想情况下,D 和 G 都会随着不断训练,做得越来越好——直到 G 基本上成为了一个“赝品制造大师”,而 D 因无法正确区分两种数据分布输给 G。
实践中,Ian Goodfellow 展示的这项技术在本质上是:G 能够对原始数据集进行一种无监督学习,找到以更低维度的方式(lower-dimensional manner)来表示数据的某种方法。而无监督学习之所以重要,就好像 Yann LeCun 的那句话:“无监督学习是蛋糕的糕体”。这句话中的蛋糕,指的是无数学者、开发者苦苦追寻的“真正的 AI”。
二、用PyTorch训练GAN
Dev Nag:在表面上,GAN 这门如此强大、复杂的技术,看起来需要编写天量的代码来执行,但事实未必如此。我们使用 PyTorch,能够在 50 行代码以内创建出简单的 GAN 模型。这之中,其实只有五个部分需要考虑:
- R:原始、真实数据集
- I:作为熵的一项来源,进入生成器的随机噪音
- G:生成器,试图模仿原始数据
- D:判别器,试图区别 G 的生成数据和 R
- 我们教 G 糊弄 D、教 D 当心 G 的“训练”环。
R:在我们的例子里,从最简单的 R 着手——贝尔曲线(bell curve)。它把平均数(mean)和标准差(standard deviation)作为输入,然后输出能提供样本数据正确图形(从 Gaussian 用这些参数获得 )的函数。在我们的代码例子中,我们使用 4 的平均数和 1.25 的标准差。
def get_distribution_sampler(mu, sigma):
return lambda n: torch.Tensor(np.random.normal(mu, sigma, (1, n))) # GaussianI:生成器的输入是随机的,为提高点难度,我们使用均匀分布(uniform distribution )而非标准分布。这意味着,我们的 Model G 不能简单地改变输入(放大/缩小、平移)来复制 R,而需要用非线性的方式来改造数据。
def get_generator_input_sampler():
return lambda m, n: torch.rand(m, n) # Uniform-dist data into generator, _NOT_ Gaussian
G: 该生成器是个标准的前馈图(feedforward graph)——两层隐层,三个线性映射(linear maps)。我们使用了 ELU (exponential linear unit)。G 将从 I 获得平均分布的数据样本,然后找到某种方式来模仿 R 中标准分布的样本。
class Generator(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Generator, self).__init__()
self.map1 = nn.Linear(input_size, hidden_size)
self.map2 = nn.Linear(hidden_size, hidden_size)
self.map3 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = F.elu(self.map1(x))
x = F.sigmoid(self.map2(x))
return self.map3(x)D: 判别器的代码和 G 的生成器代码很接近。一个有两层隐层和三个线性映射的前馈图。它会从 R 或 G 那里获得样本,然后输出 0 或 1 的判别值,对应反例和正例。这几乎是神经网络的最弱版本了。
class Discriminator(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Discriminator, self).__init__()
self.map1 = nn.Linear(input_size, hidden_size)
self.map2 = nn.Linear(hidden_size, hidden_size)
self.map3 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = F.elu(self.map1(x))
x = F.elu(self.map2(x))
return F.sigmoid(self.map3(x))最后,训练环在两个模式中变幻:第一步,用被准确标记的真实数据 vs. 假数据训练 D;随后,训练 G 来骗过 D,这里是用的不准确标记。道友们,这是正邪之间的较量。
for epoch in range(num_epochs):
for d_index in range(d_steps):
# 1. Train D on real+fake
D.zero_grad()
# 1A: Train D on real
d_real_data = Variable(d_sampler(d_input_size))
d_real_decision = D(preprocess(d_real_data))
d_real_error = criterion(d_real_decision, Variable(torch.ones(1))) # ones = true
d_real_error.backward() # compute/store gradients, but don't change params
# 1B: Train D on fake
d_gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
d_fake_data = G(d_gen_input).detach() # detach to avoid training G on these labels
d_fake_decision = D(preprocess(d_fake_data.t()))
d_fake_error = criterion(d_fake_decision, Variable(torch.zeros(1))) # zeros = fake
d_fake_error.backward()
d_optimizer.step() # Only optimizes D's parameters; changes based on stored gradients from backward()
for g_index in range(g_steps):
# 2. Train G on D's response (but DO NOT train D on these labels)
G.zero_grad()
gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
g_fake_data = G(gen_input)
dg_fake_decision = D(preprocess(g_fake_data.t()))
g_error = criterion(dg_fake_decision, Variable(torch.ones(1))) # we want to fool, so pretend it's all genuine
g_error.backward()
g_optimizer.step() # Only optimizes G's parameters即便你从没接触过 PyTorch,大概也能明白发生了什么。在第一部分,我们让两种类型的数据经过 D,并对 D 的猜测 vs. 真实标记执行不同的评判标准。这是 “forward” 那一步;随后我们需要 “backward()” 来计算梯度,然后把这用来在 d_optimizer step() 中更新 D 的参数。这里,G 被使用但尚未被训练。
在最后的部分,我们对 G 执行同样的操作——注意我们要让 G 的输出穿过 D (这其实是送给造假者一个鉴定专家来练手)。但在这一步,我们并不优化、或者改变 D。我们不想让鉴定者 D 学习到错误的标记。因此,我们只执行 g_optimizer.step()。
这就是全部了。还有一些其他样板代码,但GAN特定的东西只是那5个组件,没有别的了。
在 D 和 G 之间几千轮交手之后,我们会得到什么?判别器 D 会快速改进,而 G 的进展要缓慢许多。但当模型达到一定性能之后,G 才有了个配得上的对手,并开始提升,巨幅提升。
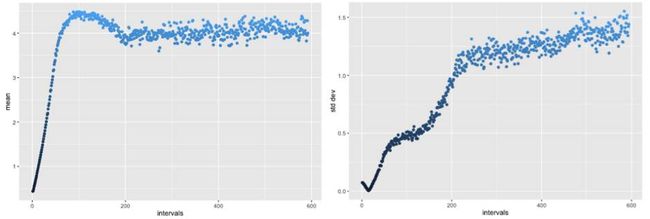
两万轮训练之后,G 的输入平均值超过 4,但会返回到相当平稳、合理的范围(左图)。同样的,标准差一开始在错误的方向降低,但随后攀升至理想中的 1.25 区间(右图),达到 R 的层次。
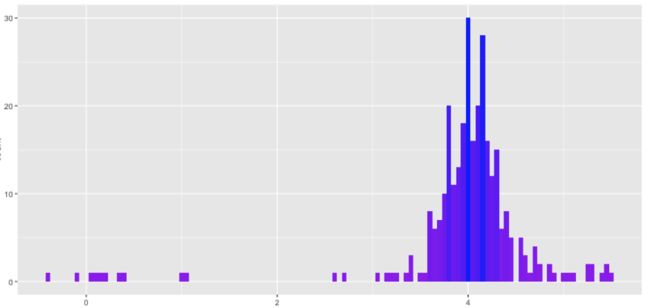
所以,基础数据最终会与 R 吻合。那么,那些比 R 更高的时候呢?数据分布的形状看起来合理吗?毕竟,你一定可以得到有 4.0 的平均值和 1.25 标准差值的均匀分布,但那不会真的符合 R。我们一起来看看 G 生成的最终分布。
结果是不错的。左侧的尾巴比右侧长一些,但偏离程度和峰值与原始 Gaussian 十分相近。G 接近完美地再现了原始分布 R——D 落于下风,无法分辨真相和假相。而这就是我们想要得到的结果——使用不到 50 行代码。
该说的都说完了,老司机请上 GitHub 把玩全套代码。
地址:https://github.com/devnag/pytorch-generative-adversarial-networks
附所有代码供参考:
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
# Data params
data_mean = 4
data_stddev = 1.25
# Model params
g_input_size = 1 # Random noise dimension coming into generator, per output vector
g_hidden_size = 50 # Generator complexity
g_output_size = 1 # size of generated output vector
d_input_size = 100 # Minibatch size - cardinality of distributions
d_hidden_size = 50 # Discriminator complexity
d_output_size = 1 # Single dimension for 'real' vs. 'fake'
minibatch_size = d_input_size
d_learning_rate = 2e-4 # 2e-4
g_learning_rate = 2e-4
optim_betas = (0.9, 0.999)
num_epochs = 30000
print_interval = 200
d_steps = 1 # 'k' steps in the original GAN paper. Can put the discriminator on higher training freq than generator
g_steps = 1
# ### Uncomment only one of these
#(name, preprocess, d_input_func) = ("Raw data", lambda data: data, lambda x: x)
(name, preprocess, d_input_func) = ("Data and variances", lambda data: decorate_with_diffs(data, 2.0), lambda x: x * 2)
print("Using data [%s]" % (name))
# ##### DATA: Target data and generator input data
def get_distribution_sampler(mu, sigma):
return lambda n: torch.Tensor(np.random.normal(mu, sigma, (1, n))) # Gaussian
def get_generator_input_sampler():
return lambda m, n: torch.rand(m, n) # Uniform-dist data into generator, _NOT_ Gaussian
# ##### MODELS: Generator model and discriminator model
class Generator(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Generator, self).__init__()
self.map1 = nn.Linear(input_size, hidden_size)
self.map2 = nn.Linear(hidden_size, hidden_size)
self.map3 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = F.elu(self.map1(x))
x = F.sigmoid(self.map2(x))
return self.map3(x)
class Discriminator(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Discriminator, self).__init__()
self.map1 = nn.Linear(input_size, hidden_size)
self.map2 = nn.Linear(hidden_size, hidden_size)
self.map3 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = F.elu(self.map1(x))
x = F.elu(self.map2(x))
return F.sigmoid(self.map3(x))
def extract(v):
return v.data.storage().tolist()
def stats(d):
return [np.mean(d), np.std(d)]
def decorate_with_diffs(data, exponent):
mean = torch.mean(data.data, 1)
mean_broadcast = torch.mul(torch.ones(data.size()), mean.tolist()[0][0])
diffs = torch.pow(data - Variable(mean_broadcast), exponent)
return torch.cat([data, diffs], 1)
d_sampler = get_distribution_sampler(data_mean, data_stddev)
gi_sampler = get_generator_input_sampler()
G = Generator(input_size=g_input_size, hidden_size=g_hidden_size, output_size=g_output_size)
D = Discriminator(input_size=d_input_func(d_input_size), hidden_size=d_hidden_size, output_size=d_output_size)
criterion = nn.BCELoss() # Binary cross entropy: http://pytorch.org/docs/nn.html#bceloss
d_optimizer = optim.Adam(D.parameters(), lr=d_learning_rate, betas=optim_betas)
g_optimizer = optim.Adam(G.parameters(), lr=g_learning_rate, betas=optim_betas)
for epoch in range(num_epochs):
for d_index in range(d_steps):
# 1. Train D on real+fake
D.zero_grad()
# 1A: Train D on real
d_real_data = Variable(d_sampler(d_input_size))
d_real_decision = D(preprocess(d_real_data))
d_real_error = criterion(d_real_decision, Variable(torch.ones(1))) # ones = true
d_real_error.backward() # compute/store gradients, but don't change params
# 1B: Train D on fake
d_gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
d_fake_data = G(d_gen_input).detach() # detach to avoid training G on these labels
d_fake_decision = D(preprocess(d_fake_data.t()))
d_fake_error = criterion(d_fake_decision, Variable(torch.zeros(1))) # zeros = fake
d_fake_error.backward()
d_optimizer.step() # Only optimizes D's parameters; changes based on stored gradients from backward()
for g_index in range(g_steps):
# 2. Train G on D's response (but DO NOT train D on these labels)
G.zero_grad()
gen_input = Variable(gi_sampler(minibatch_size, g_input_size))
g_fake_data = G(gen_input)
dg_fake_decision = D(preprocess(g_fake_data.t()))
g_error = criterion(dg_fake_decision, Variable(torch.ones(1))) # we want to fool, so pretend it's all genuine
g_error.backward()
g_optimizer.step() # Only optimizes G's parameters
if epoch % print_interval == 0:
print("%s: D: %s/%s G: %s (Real: %s, Fake: %s) " % (epoch,
extract(d_real_error)[0],
extract(d_fake_error)[0],
extract(g_error)[0],
stats(extract(d_real_data)),
stats(extract(d_fake_data))))