python实现的基于hmm模型的词性标注系统

python实现的基于hmm模型的词性标注系统

任务定义

实现一个词性标注系统，输入分好词的单词序列，输出一个词性标注后的结果序

使用的语料库为人民日报98年公开语料库，一共约18000行语料。在用户交互模式下，所有语料库均用作训练。在文件读写模式下，前3000行语句用来做测试，后面的语句用来做训练。

方法描述

隐马尔科夫模型理解

• 隐马尔科夫模型是结构最简单的动态贝叶斯网络。描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生随机序列的过程。隐藏的马尔科夫链随机生成的状态的序列称为状态序列，每个状态生成一个观测，称为观测序列。

• 隐马尔科夫做了两个基本的假设

  • 齐次马尔科夫假设，即假设隐藏的马尔科夫链在任意时刻t的状态只依赖于前一时刻的状态，去其他观测状态无关。
  • 观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态，与其他观测以及状态无关。

• 隐马尔科夫模型由初始状态概率向量π，状态转移概率矩阵A，以及观测概率矩阵B决定。

• 在词性标注问题中，初始状态概率为每个语句序列开头出现的词性的概率，状态转移概率矩阵由相邻两个单词的词性得到，观测序列为分词后的单词序列，状态序列为每个单词的词性，观测概率矩阵B也就是一个词性到单词的概率矩阵。

• 隐马尔科夫模型有三个基本问题：

  • 概率计算问题，给出模型和观测序列，计算在模型 λ 下观测序列O出现的概率
  • 学习问题，估计模型 λ=（A,B,π） 参数，使得该模型下观测序列 P(0|λ) 最大，也就是用极大似然的方法估计参数
  • 观测问题，已知模型 λ 和观测序列O，求对给的观测序列条件概率P(I|O)最大的状态序列I，即给的观测序列，求最可能的状态序列。

  在词性标注问题中，需要解决的是学习问题和观测问题。学习问题即转移矩阵的构建，观测问题即根据单词序列得到对应的词性标注序列

语料库的处理

在原始语料库中，存在多个连续空格以及空行等不便处理的字符。所以先用正则表达式对原始语料库进行处理。

由init.py文件实现，实现代码如下。

fin=codecs.open("语料.txt","r","utf-8")
strl=fin.read()
strl = re.sub("\[","",strl)
strl = re.sub("]nt","",strl)
strl = re.sub("]ns","",strl)
strl = re.sub("]nz","",strl)
strl = re.sub("]l","",strl)
strl = re.sub("]i","",strl)
strl = re.sub("\n", "@", strl)
strl = re.sub("\s+"," ", strl)
strl = re.sub("@","\n",strl)
strl = re.sub(" \n","\n",strl)
strl = re.sub(" ","@",strl)
strl = re.sub("\s+","\n",strl)
strl = re.sub("@"," ",strl)
s=strl.encode("utf-8")
fout=open("处理语料.txt","w")
fout.write(s)
fout.close()
fin.close()

学习问题

三个概率的计算是该算法的核心。

• 转移概率 aij 的计算

  aij=Aij∑Nj=1Aij

  其中 Aij 表示从t时刻到t+1时刻，从状态i变成状态j的频数

• 观测概率 bj(k) 的计算

  bj(k)=Bjk∑Mk=1Bjk

  其中 Bjk 表示状态为j，观测为k的概率

• 初始状态概率 πi 的计算

  估计为多个序列中，初始状态 qi 出现的频率

在python语言的实现中，各个矩阵的表示方法如下。

# 先验概率矩阵
pi = {}
# 状态转移概率矩阵
A = {}
# 观测概率矩阵
B = {}

先验概率矩阵是一个一维字典。状态转移概率和观测概率矩阵都是一个二维字典。统计出各个矩阵的值的方法如下。

# 所有词语
ww = []
# 所有的词性
pos = []
# 每个词性出现的频率
fre = {}
# 先验概率矩阵
pi = {}
# 状态转移概率矩阵
A = {}
# 观测概率矩阵
B = {}
# dp概率
dp = []
# 路径记录
pre = []
zz = {}
fin = codecs.open("处理语料.txt", "r", "utf-8")
while (True):
    text = fin.readline()
    if (text == ""):
        break
    tmp = text.split(" ")
    n = len(tmp)
    for i in range(0, n - 1):
        word = tmp[i].split('/')
        if (word[1] not in pos):
            pos.append(word[1])
fin = codecs.open("分词语料.txt", "r", "utf-8")
text = fin.read()
ww = text.split("\n")

n=len(pos)
#初始化概率矩阵
for i in pos:
    pi[i]=0
    fre[i]=0
    A[i]={}
    B[i]={}
    for j in pos:
        A[i][j]=0
    for j in ww:
        B[i][j]=0

#计算概率矩阵
line=0#总行数
fin=codecs.open("处理语料.txt","r","utf-8")
while(True):
    text=fin.readline()
    if(text=="\n"):
        continue
    if(text==""):
        break
    tmp=text.split(" ")
    n=len(tmp)
    line+=1
    for i in range(0,n-1):
        word=tmp[i].split('/')
        pre=tmp[i-1].split('/')
        fre[word[1]]+=1
        if(i==1):
            pi[word[1]]+=1
        elif(i > 0):
            A[pre[1]][word[1]]+=1
        B[word[1]][word[0]]+=1

cx={}
cy={}
for i in pos:
    cx[i]=0
    cy[i]=0
    pi[i]=pi[i]*1.0/line
    for j in pos:
        if(A[i][j]==0):
            cx[i]+=1
            A[i][j]=0.5
    for j in ww:
        if(B[i][j]==0):
            cy[i]+=1
            B[i][j]=0.5

for i in pos:
    pi[i]=pi[i]*1.0/line
    for j in pos:
        A[i][j]=A[i][j]*1.0/(fre[i]+cx[i])
    for j in ww:
        B[i][j]=B[i][j]*1.0/(fre[i]+cy[i])

print "训练结束"

为了解决概率矩阵稀疏的问题，最后一部分代码采用了Add-delta平滑方法，对概率矩阵进行了平滑处理。

观测问题

通常采用维比特算法来解决观测问题。本质上是一个非常简单的动态规划问题。利用 dpij 表示处理到第i个单词，该单词词性为j的序列出现的概率。由于做了齐次马尔科夫的假设，所以这样做是不会有后效性的。转移到dpi+1也十分的简单。

具体代码如下：

    num=len(text)
    for i in range(0,num):
        text[i]=unicode(text[i])
    dp=[{} for i in range(0,num)]
    pre=[{} for i in range(0,num)]
    #初始化概率
    for k in pos:
        for j in range(0,num):
            dp[j][k]=0
            pre[j][k]=""
    n=len(pos)
    for c in pos:
        if(B[c].has_key(text[0])):
            dp[0][c]=pi[c]*B[c][text[0]]*1000
        else:
            dp[0][c]=pi[c]*0.5*1000/(cy[c]+fre[c])
    for i in range(1,num):
        for j in pos:
            for k in pos:
                tt=0
                if(B[j].has_key(text[i])):
                    tt=B[j][text[i]]*1000
                else:
                    tt=0.5*1000/(cy[j]+fre[j])
                if(dp[i][j]1][k]*A[k][j]*tt):
                    dp[i][j]=dp[i-1][k]*A[k][j]*tt
                    pre[i][j]=k

一些问题和思考

• 尽管python默认支持高精度小数，但是由于转移概率矩阵很多数值太小，当遇到很长的语句时，还是会出现精度不够的情况。更好的做法是把概率取对数相加，这里我选择了简单粗暴得乘以一千，也算是简单解决了问题。
• 对于未见词选择了类似平滑的处理方式。增强了对未见词的处理能力。

性能评价

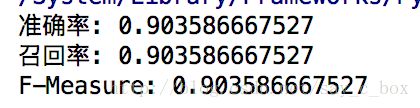
由于输入输出序列一定等长，所以准确率和回归率相等。测出数据如下所示

运行环境

python 2.7

python代码

# -*- coding: UTF-8 -*-
# 打开一个文件
# coding:utf-8


import sys

reload(sys)
sys.setdefaultencoding('utf8')
import codecs
import re
import math
from operator import itemgetter, attrgetter

# 所有词语
ww = []
# 所有的词性
pos = []
# 每个词性出现的频率
fre = {}
# 先验概率矩阵
pi = {}
# 状态转移概率矩阵
A = {}
# 观测概率矩阵
B = {}
# dp概率
dp = []
# 路径记录
pre = []

zz = {}

fin = codecs.open("处理语料.txt", "r", "utf-8")
while (True):
    text = fin.readline()
    if (text == ""):
        break
    tmp = text.split(" ")
    n = len(tmp)
    for i in range(0, n - 1):
        word = tmp[i].split('/')
        if (word[1] not in pos):
            pos.append(word[1])
fin = codecs.open("分词语料.txt", "r", "utf-8")
text = fin.read()
ww = text.split("\n")

n=len(pos)
#初始化概率矩阵
for i in pos:
    pi[i]=0
    fre[i]=0
    A[i]={}
    B[i]={}
    for j in pos:
        A[i][j]=0
    for j in ww:
        B[i][j]=0

#计算概率矩阵
line=0#总行数
fin=codecs.open("处理语料.txt","r","utf-8")
while(True):
    text=fin.readline()
    if(text=="\n"):
        continue
    if(text==""):
        break
    tmp=text.split(" ")
    n=len(tmp)
    line+=1
    for i in range(0,n-1):
        word=tmp[i].split('/')
        pre=tmp[i-1].split('/')
        fre[word[1]]+=1
        if(i==1):
            pi[word[1]]+=1
        elif(i > 0):
            A[pre[1]][word[1]]+=1
        B[word[1]][word[0]]+=1

cx={}
cy={}
for i in pos:
    cx[i]=0
    cy[i]=0
    pi[i]=pi[i]*1.0/line
    for j in pos:
        if(A[i][j]==0):
            cx[i]+=1
            A[i][j]=0.5
    for j in ww:
        if(B[i][j]==0):
            cy[i]+=1
            B[i][j]=0.5

for i in pos:
    pi[i]=pi[i]*1.0/line
    for j in pos:
        A[i][j]=A[i][j]*1.0/(fre[i]+cx[i])
    for j in ww:
        B[i][j]=B[i][j]*1.0/(fre[i]+cy[i])

print "训练结束"

while(True):
    tmp=raw_input("请输入需要词性标注的句子，以空格分割: ")
    if(tmp=="-1"):
        break
    text=tmp.split(" ")

    num=len(text)
    for i in range(0,num):
        text[i]=unicode(text[i])
    dp=[{} for i in range(0,num)]
    pre=[{} for i in range(0,num)]
    #初始化概率
    for k in pos:
        for j in range(0,num):
            dp[j][k]=0
            pre[j][k]=""
    n=len(pos)
    for c in pos:
        if(B[c].has_key(text[0])):
            dp[0][c]=pi[c]*B[c][text[0]]*1000
        else:
            dp[0][c]=pi[c]*0.5*1000/(cy[c]+fre[c])
    for i in range(1,num):
        for j in pos:
            for k in pos:
                tt=0
                if(B[j].has_key(text[i])):
                    tt=B[j][text[i]]*1000
                else:
                    tt=0.5*1000/(cy[j]+fre[j])
                if(dp[i][j]1][k]*A[k][j]*tt):
                    dp[i][j]=dp[i-1][k]*A[k][j]*tt
                    pre[i][j]=k
    res={}
    MAX=""
    for j in pos:
        if(MAX=="" or dp[num-1][j]>dp[num-1][MAX]):
            MAX=j
    if(dp[num-1][MAX]==0):
        print "您的句子超出我们的能力范围了"
        continue
    i=num-1
    while(i>=0):
        res[i]=MAX
        MAX=pre[i][MAX]
        i-=1
    for i in range(0,num):
        print text[i].decode('utf-8')+"\\"+res[i].decode('utf-8'),
    print ""