从HMM到CRF到LSTM+CRF
在实习的时候有用到LSTM+CRF,但以前对HMM、CRF理论了解的不多,导致自己在理论方面有所欠缺。因此特此写一篇从HMM到CRF再到LSTM+CRF中的非纯理论性质的文章,算是一个阶段性笔记和总结。
本文的侧重点还是以LSTM+CRF为主,对于LSTM+CRF中依赖到的HMM、CRF中的概念会做详细说明,主要包含几个部分:
- 马尔科夫模型
- 隐马尔科夫模型(HMM)
- HMM中的前向算法
- 维特比算法(viterbe)
- 条件随机场(CRF)
- CRF中的矩阵表示
- CRF中的前向算法
- LSTM+CRF模型
- LSTM+CRF中CRF层
- 源码解析
本文长而杂,阅读须谨慎。
0. Markov Model
之前也看过隐马尔科夫模型,也知道它有转移矩阵A、观测矩阵B。但是看完没多久又忘了,又说不出。所以还是概念不清楚。这里再巩固下。
在隐马尔科夫模型前,先忘掉HMM中的状态或观测的概念,先引入马尔科夫模型的概念。
假设我们有一个随机变量序列 X=(X1,X2,...,XT) X = ( X 1 , X 2 , . . . , X T ) , 它们的取值都来自一个状态集合 S={s1,s2,...,s|S|} S = { s 1 , s 2 , . . . , s | S | } ,将状态值带入到随机变量序列中我们就得到了一个长度为 T T 的状态序列。以天气系统为例, S={sun,cloud,rain} S = { s u n , c l o u d , r a i n } , |S|=3 | S | = 3 ,当观测长度为 T=3 T = 3 时,可能的一个状态序列为 {X1=ssun,X2=scloud,X3=srain} { X 1 = s s u n , X 2 = s c l o u d , X 3 = s r a i n } 。
上面的状态序列,在马尔科夫模型中做了两个假设:
Limited Horizon:
P(St+1=sk∣X1,X2,...,Xt)=P(St+1=sk∣Xt) P ( S t + 1 = s k ∣ X 1 , X 2 , . . . , X t ) = P ( S t + 1 = s k ∣ X t )即下一个状态的输出概率只与上一个状态有关
Time Invariant
P(St+1=sk∣Xt)=P(X2=sk∣X1) P ( S t + 1 = s k ∣ X t ) = P ( X 2 = s k ∣ X 1 )即状态 St+1 S t + 1 与 St S t 输出概率之间的关系与时刻t无关,不会应为时刻不同而改变。
在马尔科夫模型中,为了确定状态到状态的转移概率,因此我们需要定义状态转移矩阵 A A ,而在状态到达初始时刻则需要定义初始状态概率向量 π π 。
下面以一个例子说明马尔科夫模型:
(1) 记状态序列为
(2) 初始状态概率为
(3) 转移矩阵为
对应的转移状态图为
则状态序列为1011的概率为:
从上面这个例子可以看到,马尔科夫模型只能解决简单的状态转移问题。也即我观测到了一个状态序列,同时我知道状态间如何转移,那么我就知道整个状态产生的概率。但如果我们无法观测到这个状态序列,该怎么办?
一个典型的例子就是Ice Cream Climatology问题,我想预测一段时间的气候是HOT还是COLD,但是我我无法观测到这段时间的气候是什么,我只能观测到我每天吃了多少个冰激凌。因此对我来说,气候就是个隐含序列,真正的观测序列是我这段时间吃的冰激凌数目序列。
另一个例子就是NLP中词性标注(POS Tagging)问题,我有两个序列,一个是句子序列,一个是句子中每个词的词性构成的标记序列。但实际中我通常只有句子序列,在预测前词性无法得知,因此词性就是个隐含序列。
当实际问题中即包含观测序列又包含隐含的状态序列时,就需要隐马尔科夫了。
1. Hidden Markov Model
隐马尔科夫模型包含两个序列,一个状态序列 Q={q1,q2,...,qn} Q = { q 1 , q 2 , . . . , q n } ,一个观测序列 O={o1,o2,...,on} O = { o 1 , o 2 , . . . , o n } ,每个状态 qi q i 生成一个观测 oi o i 。在隐马尔科夫模型中,做了一个输出独立的假设:
即t时刻的观测值只依赖于t时刻的状态,与其他时刻状态无关。符号系统我沿用了《统计学习方法》。
隐马尔科夫模型同样需要初始向量 π π ,状态转移矩阵 A A 。由于我们多引入了一个观测序列,因此需要额外定义一个观测概率矩阵 B B ,用于描述某个状态 qt q t 产生某个观测值 ot o t 的概率。 λ=(A,B,π) λ = ( A , B , π ) 即模型的参数。
在隐马尔科夫模型中,有3个基本问题,这里我主要描述其中的两个:
(1) 概率计算问题:给定模型 λ=(A,B,π) λ = ( A , B , π ) 和观测序列 O={o1,o2,...,on} O = { o 1 , o 2 , . . . , o n } ,求观测 O O 出现的概率 P(O|λ) P ( O | λ )
(2) 预测问题:给定模型 λ=(A,B,π) λ = ( A , B , π ) 和观测序列 O={o1,o2,...,on} O = { o 1 , o 2 , . . . , o n } ,求条件概率 P(I∣O) P ( I ∣ O ) 最大的隐含状态序列 I={ii,i2,...,iT} I = { i i , i 2 , . . . , i T }
1.1 前向算法
求观测序列 O O 出现的概率的一种方式是求出所有状态序列 I I 产生观测序列 O O 的概率。这里要求出所有可能的状态序列是不可行的。思路是对的,但是有种更高效的计算方式。记前向概率为:
表示到t时刻部分观测序列为 o1,o2,...,ot o 1 , o 2 , . . . , o t 且状态为 qi q i 的概率。即t-1时刻的所有状态转移到t时刻的状态 it=qi i t = q i 并生成 ot o t 的概率。对于 it+1=qj i t + 1 = q j 的状态也是如此,为t时刻所有状态转移到 qj q j 并在 qj q j 生成 ot+1 o t + 1 的概率。如图
计算后一时刻概率时,前一时刻的概率是可以复用的。前向算法就是这样的算法,它快速的地方就是每次计算直接引用前一个时刻的计算结果,避免重复计算。我参照《统计学习方法》例10.2写了个简单的实现
import time
import numpy as np
A = np.array([[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]])
B = np.array([[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]])
PI = np.array([0.2, 0.4, 0.4])
def forward(obs):
alpha_t = PI * B[:, obs[0]]
for t in range(1, len(A)):
# 计算t-1时刻所有节点到t时刻y中某一个节点的概率
transition_score = np.dot(alpha_t, A)
emission_score = B[: ,obs[t]]
alpha_t = transition_score * emission_score
po = np.sum(alpha_t)
print("P(O|lambda): {}".format(po))
return po
if __name__ == '__main__':
obs = [0, 1, 0] # red white red
forward(obs)1.2 预测算法
对于词性标注任务来说,即已知句子序列 O O ,那这个句子最可能的词性序列 I I 是什么?预测算法就是要求一个词性序列 I I ,这个序列具有最大的条件概率 P(I∣O) P ( I ∣ O ) 。
假设在t时刻观测值为 ot o t ,此时状态为 r r 。在t-1时刻处于状态 s s , s s 的取值分别为 i,j,k i , j , k ,由状态 s s 转移到状态 r r 并产生 ot o t 的概率可以描述为:
假设状态 s=i,j,k s = i , j , k 的概率为 ci,cj,ck c i , c j , c k ,那么上述概率用图示即为:
由t-1时刻的状态 s s 到t时刻的状态 r r 的的路径有三条,这三条都有可能是最优的状态路径,那么经过 r r 后会传递出3条可能的状态序列,假设t+1时刻有三个状态,那么在t+1时刻的状态序列就有 3×3=32 3 × 3 = 3 2 种可能,可能的状态序列以指数传播。
在viterbi算法中,就不一样了。既然 s s 到 r r 有三条可能的路径,那就计算这三条状态序列的概率,保留概率最大的那条。如图:
这样每个状态就只会传递一个序列下去,而不是N个,就不会使序列数量呈指数成长。
为什么只要保留到当前节点的最优那条路径就可以了呢?再如图:
假设S->E的最优路径为S->A2->B2->C2->E,且这条路径经过C2,那么对于S->C2的其他所有子路径来说,S->A2->B2->C2这条子路径一定是最优的。如果这条路径不是最优的,比如有另一条路径S->A1->B1->C2更优,那么用这条路径替换S->A2->B2->C2,那么原先S->E的最优路径就不是S->A2->B2->C2->E,这与我们的假设矛盾。上面的证明说明“全局最短”路径必定经过在这些“局部最短”子路径。因此,每个节点只保留到自己的局部最优路径即可。
参照《统计学习方法》例10.3,我也写了个简单实现:
import time
import numpy as np
A = np.array([[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]])
B = np.array([[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]])
PI = np.array([0.2, 0.4, 0.4])
def viterbi(obs):
state = PI * B[:, obs[0]]
# 记录到达当前state(t时刻)且具有最优路径概率的state_index(t-1时刻)
sequence_indices = np.zeros((len(obs), len(A)), dtype=np.int32)
# viterbi前向计算
for t in range(1, len(obs)):
state = state.reshape(-1, 1)
# 计算每个状态最优路径的概率
transition_score = (state * A).max(axis=0)
sequence_indices[t] = (state * A).argmax(axis=0)
state = transition_score * B[:, obs[t]]
# 反向查找最优状态序列
final_sequence = [state.argmax()]
for t in range(len(obs)-1, 0, -1):
state_index = sequence_indices[t][final_sequence[-1]]
final_sequence.append(state_index)
print("final_sequence: {}".format(final_sequence[::-1]))
return final_sequence[::-1]
if __name__ == '__main__':
obs = [0, 1, 0] # red white red
viterbi(obs)2. Conditional Random Field
条件随机场的理论要讲起来一篇内容可能很难覆盖到,而且理论太多让人看起来容易睡着。我这里就简单引入一下,前面几段可能会非常无聊,但还是有必要讲下。关于定义和符号系统仍沿用《统计学习方法》,我会对书中表述有问题的做一定的修正和说明。在后面LSTM+CRF的部分,也会涉及到这节的内容。
2.1 CRF
设 X X 与 Y Y 是随机变量, P(Y∣X) P ( Y ∣ X ) 是给定 X X 时 Y Y 的条件概率分布,若随机变量 Y Y 构成的是一个马尔科夫随机场,则称条件概率分布 P(Y∣X) P ( Y ∣ X ) 是条件随机场。
2.2 Linear-Chain CRF
(1) 定义
在词性标注等问题中,我们通常使用条件随机场的特例——线性链条件随机场,因此我这里主要关注线性链条件随机场,定义为:
设 X=(X1,X2,...,Xn) X = ( X 1 , X 2 , . . . , X n ) , Y=(Y1,Y2,...,Yn) Y = ( Y 1 , Y 2 , . . . , Y n ) 均为线性链表示的随机变量序列,在给定随机变量序列 X X 的条件下,随机变量序列 Y Y 的条件概率分布 P(Y|X) P ( Y | X ) 构成条件随机场,即满足马尔科夫性:
则称 P(Y∣X) P ( Y ∣ X ) 为线性链条件随机场。
(2) 模型表示
线性链条件随机场对 P(Y∣X) P ( Y ∣ X ) 建模,表示为:
其中:
tk t k 和 sl s l 是特征函数, λk λ k 和 μl μ l 为对应权重。 Z(x) Z ( x ) 的求和是在所有可能的输出序列上进行。
(3) 简化形式
如果将上述 K1 K 1 个转移特征函数和 K2 K 2 个状态特征函数写在一起有:
其中: K=K1+K2 K = K 1 + K 2 。
wk w k 将 λk λ k 和 μl μ l 整合在一起,定义为:
fk f k 将 tk t k 和 sl s l 整合在一起,定义为:
对 fk(yi−1,yi,x,i) f k ( y i − 1 , y i , x , i ) 在各时序位置 i i 求和,有:
(4) 矩阵表示
到这里就是重点了,因为LSTM+CRF的模型是基于矩阵形式求解的。矩阵形式的表示不仅表达简洁,而且我们发现这样表达后它和HMM的表达形式越发的像。
首先,在序列前后引入起点和终点标记: y0=start y 0 = s t a r t , yn+1=stop y n + 1 = s t o p 。同时定义一个 m×m m × m 的矩阵 Mi(x) M i ( x ) 。其中, m m 为标记 y y 的取值个数, i=1,2,...,n+1 i = 1 , 2 , . . . , n + 1 ,那么有:
经过上面三个公式表示,有:
看完上面一堆公式后有两个问题:
1. Mi(x) M i ( x ) 这个矩阵到底是什么样的?
2. 为什么 Zw(x) Z w ( x ) 可以表示为多个矩阵相乘?
对于第1个问题,假设标记 y y 可能的取值为 {1,2,3} { 1 , 2 , 3 } ,加上引入的 y0=start y 0 = s t a r t 和 yn+1=stop y n + 1 = s t o p , Mi(x) M i ( x ) 为5阶矩阵。按照《统计学习方法》和CRF原论文的表达, Mi(x) M i ( x ) 应该表示如下:
对于第2个问题, Zw(x) Z w ( x ) 中的求和是在所有可能的输出序列 y y 上进行的, M1(x)×M2(x)×...Mn+1(x) M 1 ( x ) × M 2 ( x ) × . . . M n + 1 ( x ) 带入 Mi(yi−1,yi∣x) M i ( y i − 1 , y i ∣ x ) ,每个矩阵的乘积就变成原公式中的指数相加,而前 i i 个矩阵的乘积代表了标记序列 y y 从时刻1到t的所有可能的组合。n+1个矩阵相乘得到的矩阵 M(x) M ( x ) 为:
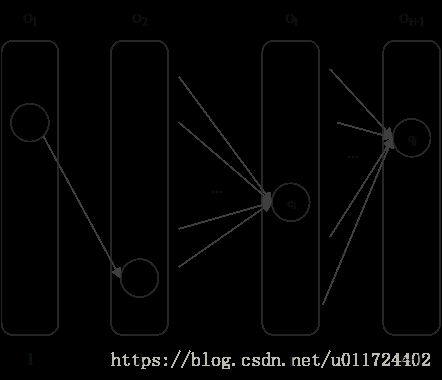
对矩阵 M(x) M ( x ) 取第start行stop列就得到了 Zw(x) Z w ( x ) 。有时候为了方便,可以去掉上面矩阵中的0元素,这样 M1(x) M 1 ( x ) 为行向量, Mn+1(x) M n + 1 ( x ) 为列向量,n+1个矩阵相乘得到的标量即 Zw(x) Z w ( x ) 。用图来表示上述过程如下:
图中的矩阵 Mi(x) M i ( x ) 与HMM中的转移矩阵非常相似。
(5) 概率计算
这里我只对前向算法做以说明,通过前向算法可以求出任意时刻 y y 的非规范化概率。
对每个位置 i=0,1,...,n+1 i = 0 , 1 , . . . , n + 1 ,定义前向向量 αi(x) α i ( x ) :
假设标记 y y 有3种可能的取值,加上 start s t a r t 和 stop s t o p , α0(x) α 0 ( x ) 为5维列向量, αT0(x)=[1,0,0,0,0] α 0 T ( x ) = [ 1 , 0 , 0 , 0 , 0 ] 。
递推公式为:
又可表示为 公式(1):
ai(yi∣x) a i ( y i ∣ x ) 表示在位置 i i 的标记是 yi y i 并且到位置 i i 的前部分标记序列的非规范化概率。通俗点就是到 i i 时刻,标记 yi y i 下的累积概率。当计算到 n n 时刻的累积概率 αn(x) α n ( x ) 时,那么有规范化因子 Zw(x)=αTn(x)⋅1 Z w ( x ) = α n T ( x ) ⋅ 1 ,这里的前向算法和前面分析求解 Zw(x) Z w ( x ) 的过程是类似的。
再借用上图,可以看到上图就是个多层的NN,网络由多个hidden layer构成,每一个hidden layer的输出即为 αn(x) α n ( x ) ,下一层的权重矩阵为 Mi+1(x) M i + 1 ( x ) 。
3. LSTM+CRF
在用深度学习去解决命名实体预测(NER)时,一般是LSTM+Softmax的架构,这种架构的缺点是不考虑预测序列的Label之间的关系,以词性标注为例,动词后面不可能再接动词,而CRF可以考虑相邻Label之间的关系。在《Neural Architectures for Named Entity Recognition》中使用了LSTM+CRF的网络结构去解决实体识别的问题,如下图。但是论文中对如何将LSTM的结果应用到CRF中讲的比较少,因此我参考了下tensorflow的crf层的实现。
3.1 定义
首先,先看下论文中的公式定义:
对于给定的输入 X=(x1,x2,...,xn) X = ( x 1 , x 2 , . . . , x n ) ,经过LSTM层后得到输出 P∈Rn×k P ∈ R n × k ,其中 k k 为实体标记的数目, Pi,j P i , j 为第 i i 个词被预测为实体 j j 的分数。
对于一条标记序列 y=(y1,y2,...,yn) y = ( y 1 , y 2 , . . . , y n ) ,定义:
其中, A A 为转移矩阵,添加start和end标记后,那么 A A 变为 k+2 k + 2 阶方阵。 Ai,j A i , j 为从标记 i i 转移到标记 j j 的分数。对分数 s(X,y) s ( X , y ) 取Softmax做规范化,则得到 y y 的预测概率:
其中,分母表示对所有可能的标记序列的分数求和。
在训练时,会最大化 log(p(y∣X)) l o g ( p ( y ∣ X ) ) :
3.2 模型实现
在tensorflow的crf.py实现中,有几个函数需要重点关注:
# 1 计算公式(4), log(p(y| X))
crf_log_likelihood(inputs, tag_indices, sequence_lengths)
# 1.1 计算公式(4)中的第一项s(X, y), 即公式(2)
crf_sequence_score(inputs, tag_indices, sequence_lengths, transition_params)
# 1.1.1 计算公式(2)中的第一项
crf_unary_score(tag_indices, sequence_lengths, inputs)
# 1.1.2 计算公式(2)中的第二项
crf_binary_score(tag_indicese, sequence_lengths, transition_params)
# 1.2 计算公式(4)中的第二项log(sum)
crf_log_norm(inputs, sequence_lengths, transition_params)
# 1.3 用于预测,输出具有最大p(y| X)条件概率的标记序列y
viterbi_decode(score, transition_params)#1 crf_log_likelihood:入口函数,接收的inputs为LSTM的输出,计算公式(4)中的两项,对应内部调用的两个方法crf_sequence_score和crf_log_norm。
def crf_log_likelihood(inputs, tag_indices, sequence_lengths, transition_params):
num_tags = inputs.get_shape()[2].value
if transition_params is None:
transition_params = vs.get_variable("transitions", [num_tags, num_tags])
sequence_scores = crf_sequence_score(inputs, tag_indices, sequence_lengths,
transition_params)
log_norm = crf_log_norm(inputs, sequence_lengths, transition_params)
# Normalize the scores to get the log-likelihood per example.
log_likelihood = sequence_scores - log_norm
return log_likelihood, transition_params#1.1 crf_sequence_score:计算公式(4)中的第一项,即 s(X,y) s ( X , y ) 。
s(X,y) s ( X , y ) 中的第一项和 yi y i 有关,被称为unary score,第二项和 yi,yi+1 y i , y i + 1 有关,被称为binary score。unary score + binary score即 s(X,y) s ( X , y ) 。在CRF中有转移特征和状态特征的概念,状态特征函数与 yi y i 有关,转移特征函数与 yi,yi+1 y i , y i + 1 有关。在tensorflow的实现中,没有特征函数的概念,只是会计算unary score和binary score。其中,LSTM的输出表示的是每个词在不同标记 y y 上的分数,与前一时刻的 y y 无关。因此,LSTM的输出会被用来计算unary score,在概念上可以视为CRF中的状态特征函数。而计算binary score时(即转移分数),会使用定义的transition_params,在概念上可以视为CRF中的转移特征函数。
def crf_sequence_score(inputs, tag_indices, sequence_lengths,
transition_params):
def _single_seq_fn():
# ...
def _multi_seq_fn():
# Compute the scores of the given tag sequence.
unary_scores = crf_unary_score(tag_indices, sequence_lengths, inputs)
binary_scores = crf_binary_score(tag_indices, sequence_lengths,
transition_params)
sequence_scores = unary_scores + binary_scores
return sequence_scores
return utils.smart_cond(
pred=math_ops.equal(inputs.shape[1].value or array_ops.shape(inputs)[1],1),
true_fn=_single_seq_fn,
false_fn=_multi_seq_fn)#1.1.1 crf_unary_score:计算公式(2)中的一元分数。
这个函数接收一个输入inputs,即LSTM对应的输出。比如LSTM的输出为:
这里我们假设句子长度为3,最长句子为4,这里做了1个padding。其中,num_tags=3。行表示句子中的词,列表示词输入某个标记y的score。记:这个句子真实的标记序列 tag_indices=[1,2,2,0] t a g _ i n d i c e s = [ 1 , 2 , 2 , 0 ] , 那么这个句子的unary score = 第一个词属于tag=1的score + 第二个词属于tag=2的score + 第三个词属于tag=2的score。那么有unary score = 5 + 3 + 4 = 12。我们在上面中时在2D矩阵中计算的,而下面的源码实现中将2D矩阵flatten为1D矩阵进行计算,最后根据mask,去掉padding部分的结果。
def crf_unary_score(tag_indices, sequence_lengths, inputs):
batch_size = array_ops.shape(inputs)[0]
max_seq_len = array_ops.shape(inputs)[1]
num_tags = array_ops.shape(inputs)[2]
flattened_inputs = array_ops.reshape(inputs, [-1])
offsets = array_ops.expand_dims(
math_ops.range(batch_size) * max_seq_len * num_tags, 1)
offsets += array_ops.expand_dims(math_ops.range(max_seq_len) * num_tags, 0)
# Use int32 or int64 based on tag_indices' dtype.
if tag_indices.dtype == dtypes.int64:
offsets = math_ops.to_int64(offsets)
flattened_tag_indices = array_ops.reshape(offsets + tag_indices, [-1])
unary_scores = array_ops.reshape(
array_ops.gather(flattened_inputs, flattened_tag_indices),
[batch_size, max_seq_len])
masks = array_ops.sequence_mask(sequence_lengths,
maxlen=array_ops.shape(tag_indices)[1],
dtype=dtypes.float32)
unary_scores = math_ops.reduce_sum(unary_scores * masks, 1)
return unary_scores#1.1.2 crf_binary_score:计算公式(2)中的二元分数。
二元分数中涉及 yi,yi+1 y i , y i + 1 ,因此涉及到转移矩阵transition_params,定义在#1.的函数中,如果我们没有传入,则内部会帮我们创建,作为一个trainable的parameter,随模型一起训练。这里假设转移矩阵为:
在实现中并没有加入start和stop,不影响结果。同样是刚才的例子, tag_indices=[1,2,2,0] t a g _ i n d i c e s = [ 1 , 2 , 2 , 0 ] ,那么binary score = 1->2的score + 2->2的score = 1 + 3 = 4。同样,我们是在2D矩阵中计算的,源码中将2D矩阵flatten到1D去gather每个位置的score,最后求和得到最终结果。
def crf_binary_score(tag_indices, sequence_lengths, transition_params):
# Get shape information.
num_tags = transition_params.get_shape()[0]
num_transitions = array_ops.shape(tag_indices)[1] - 1
# Truncate by one on each side of the sequence to get the start and end
# indices of each transition.
start_tag_indices = array_ops.slice(tag_indices, [0, 0],
[-1, num_transitions])
end_tag_indices = array_ops.slice(tag_indices, [0, 1], [-1, num_transitions])
# Encode the indices in a flattened representation.
flattened_transition_indices = start_tag_indices * num_tags + end_tag_indices
flattened_transition_params = array_ops.reshape(transition_params, [-1])
# Get the binary scores based on the flattened representation.
binary_scores = array_ops.gather(flattened_transition_params,
flattened_transition_indices)
masks = array_ops.sequence_mask(sequence_lengths,
maxlen=array_ops.shape(tag_indices)[1],
dtype=dtypes.float32)
truncated_masks = array_ops.slice(masks, [0, 1], [-1, -1])
binary_scores = math_ops.reduce_sum(binary_scores * truncated_masks, 1)
return binary_scores#1.2 crf_log_norm:计算公式(4)中的第二项log(sum),重点在CrfForwardRnnCell中,通过前向传播来计算log(sum)。
def crf_log_norm(inputs, sequence_lengths, transition_params):
"""Computes the normalization for a CRF.
Args:
inputs: A [batch_size, max_seq_len, num_tags] tensor of unary potentials
to use as input to the CRF layer.
sequence_lengths: A [batch_size] vector of true sequence lengths.
transition_params: A [num_tags, num_tags] transition matrix.
Returns:
log_norm: A [batch_size] vector of normalizers for a CRF.
"""
# Split up the first and rest of the inputs in preparation for the forward
# algorithm.
first_input = array_ops.slice(inputs, [0, 0, 0], [-1, 1, -1])
first_input = array_ops.squeeze(first_input, [1])
# If max_seq_len is 1, we skip the algorithm and simply reduce_logsumexp over
# the "initial state" (the unary potentials).
def _single_seq_fn():
return math_ops.reduce_logsumexp(first_input, [1])
def _multi_seq_fn():
"""Forward computation of alpha values."""
rest_of_input = array_ops.slice(inputs, [0, 1, 0], [-1, -1, -1])
# Compute the alpha values in the forward algorithm in order to get the
# partition function.
forward_cell = CrfForwardRnnCell(transition_params)
_, alphas = rnn.dynamic_rnn(
cell=forward_cell,
inputs=rest_of_input,
sequence_length=sequence_lengths - 1,
initial_state=first_input,
dtype=dtypes.float32)
log_norm = math_ops.reduce_logsumexp(alphas, [1])
return log_norm
max_seq_len = array_ops.shape(inputs)[1]
return control_flow_ops.cond(pred=math_ops.equal(max_seq_len, 1),
true_fn=_single_seq_fn,
false_fn=_multi_seq_fn)前向计算log(sum),对应 (5)概率计算 一节的前向算法的计算,是在log空间完成的,__call__方法中使用reduce_logsumexp来计算,在sumexp之后套了一层log,保证计算在log空间完成。具体的细节可以参见博文《 Neural Architectures for Named Entity Recognition》中的 crf 层详解。
class CrfForwardRnnCell(rnn_cell.RNNCell):
def __init__(self, transition_params):
self._transition_params = array_ops.expand_dims(transition_params, 0)
self._num_tags = transition_params.get_shape()[0].value
def __call__(self, inputs, state, scope=None):
state = array_ops.expand_dims(state, 2)
# This addition op broadcasts self._transitions_params along the zeroth
# dimension and state along the second dimension. This performs the
# multiplication of previous alpha values and the current binary potentials
# in log space.
transition_scores = state + self._transition_params
new_alphas = inputs + math_ops.reduce_logsumexp(transition_scores, [1])
# Both the state and the output of this RNN cell contain the alphas values.
# The output value is currently unused and simply satisfies the RNN API.
# This could be useful in the future if we need to compute marginal
# probabilities, which would require the accumulated alpha values at every
# time step.
return new_alphas, new_alphas由于这个__call__方法的计算看起来不那么直观,我写了一版稍微直观一点的:
def crf_log_norm(inputs, sequence_lengths, transition_params):
first_input = array_ops.slice(inputs, [0, 0, 0], [-1, 1, -1])
first_input = array_ops.squeeze(first_input, [1])
def _multi_seq_fn():
rest_of_input = array_ops.slice(inputs, [0, 1, 0], [-1, -1, -1])
forward_cell = CrfForwardRnnCell(transition_params)
_, alphas = rnn.dynamic_rnn(
cell=forward_cell,
inputs=rest_of_input,
sequence_length=sequence_lengths - 1,
initial_state=math_ops.exp(first_input), # alpha_0
dtype=dtypes.float32)
log_norm = math_ops.log(math_ops.reduce_sum(alphas, [1])) # 最后取log
return log_norm
return _multi_seq_fn()
class CrfForwardRnnCell(rnn_cell.RNNCell):
def __init__(self, transition_params):
self._transition_params = transition_params
self._num_tags = transition_params.get_shape()[0].value
# 前向算法的计算
def __call__(self, inputs, state, scope=None):
# 计算矩阵M_{i+1}(x)
mi = math_ops.exp(inputs + self._transition_params)
# 计算alpha_{i+1}(x) = alpha_i(x) * M_{i+1}(x)
new_alphas = math_ops.matmul(state, mi)
return new_alphas, new_alphas其实实现的方式挺多的,如果有人知道源码中为何要通过reduce_logsumexp来计算的话,也烦请告知下。
#1.3 viterbi_decode:用于预测,输出具有最大 p(y∣X) p ( y ∣ X ) 条件概率的标记序列 y y ,和前面HMM中的viterbi的实现思路类似,这里就不展开了。
def viterbi_decode(score, transition_params):
trellis = np.zeros_like(score)
backpointers = np.zeros_like(score, dtype=np.int32)
trellis[0] = score[0]
for t in range(1, score.shape[0]):
v = np.expand_dims(trellis[t - 1], 1) + transition_params
trellis[t] = score[t] + np.max(v, 0)
backpointers[t] = np.argmax(v, 0)
viterbi = [np.argmax(trellis[-1])]
for bp in reversed(backpointers[1:]):
viterbi.append(bp[viterbi[-1]])
viterbi.reverse()
viterbi_score = np.max(trellis[-1])
return viterbi, viterbi_score4. 总结
至此,我们大致了解了LSTM+CRF具体是怎么实现了。自LSTM+CRF的结构出现后,现在做NER的问题基本都是在原架构的基础上做了些改动,当时在搜Paper时也没搜到效果更好的方案,可能是CRF层确实很强力。
另外,tensorflow确实帮我们封装了一些很好用的方法,即使我们不懂原理但只要会调就好了,岂不是像煮青蛙一样。
So we’II still have to go to deeper levels if we’re trying something new…
5. 参考
- 《统计学习方法》10、11章
- 统计学习方法勘误 link
- 介绍HMM的两篇文章,通俗易懂。link1 link2
- 介绍Viterbe算法的文章。link
- 《条件随机场理论综述》论文。link
- 针对《统计学习方法》CRF相关部分的纠错和更为详细的说明。 link
- 《Neural Architectures for Named Entity Recognition》论文,使用LSTM+CRF结构做NER link
- Tensorflow的CRF实现源码详解 link