【论文精读】门控图神经网络GGNN及SRGNN

GGNN

SRGNN是GGNN在推荐系统上的应用，核心网络几乎没有改变。GGNN的核心模型其实非常简单，在计算上和GRU基本没有区别。但为了更好的理解$a_v$是如何构造出来的，我们还得从最基本的思想讲起。

信息传播

绝大多数GNN的思想在于消息传播(Message Passing)或者说信念传播(Belief Propagation)。很自然的，我们知道一个节点的信息可以根据其邻居节点信息进行更新。

初代GNN

2009年最早的GNN论文¹将这个过程抽象为

${\mathbf{x}}_n=f_{\mathbf{w}}\left({\mathbf{l}}_n,{\mathbf{l}}_{\mathrm{c}\mathrm{o}[n]},{\mathbf{x}}_{\mathrm{n}\mathrm{e}[n]},{\mathbf{l}}_{\mathrm{n}\mathrm{e}[n]}\right)$

其中，
$\mathbf{x}$为状态向量state，GGNN的记号$\mathbf{h}$更符合现在的习惯
$\mathbf{l}$为特征向量feature，或者说embedding
$co[n]$为与节点n相连的边，
$ne[n]$为节点n邻居节点.

以商品为例，商品的类别、价格、品质等具体属性可以组合为节点的特征向量，用户对商品的点击次数、停留时间等可以组合为边的特征向量。当然，hidden state ${\mathbf{x}}_{\mathrm{n}\mathrm{e}[n]}$本身也包含了embedding ${\mathbf{l}}_{\mathrm{n}\mathrm{e}[n]}$的信息，只保留一个，直接把 $\mathbf{l}$ 作为初始的embeding也是可以的。

根据巴拿赫不动点定理，我们利用$f_{\mathbf{w}}$不断压缩，得到稳定状态的hidden state，然后再通过$g_{\mathbf{w}}$输出.

${\mathbf{o}}_n=g_{\mathbf{w}}\left({\mathbf{x}}_n,{\mathbf{l}}_n\right)$

GNN将这两个映射函数设计为两个不同的前馈神经网络，

$f_{\mathbf{w}}$的层数，或者说迭代次数并非固定，当${\mathbf{x}}_n$达到收敛时停止，和RNN decoder输出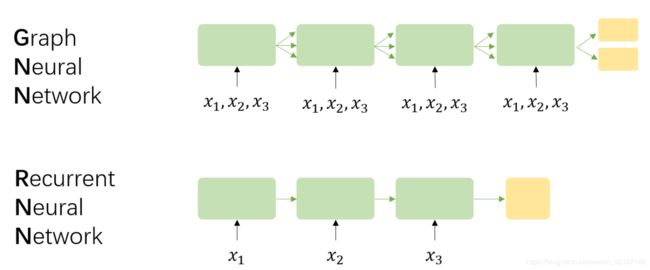时跳出循环有点类似，当然也有所不同²。
（f和w只要保证压缩映射即可，但笔者总感觉这样的网络结构并不优雅）

之后的GNN大都脱离这篇论文的原理，转向借鉴CNN/RNN的经验。

GGNN

事实上，我们很容易得到一个朴素的思想：节点的信息可以根据邻居节点的信息取平均得到（当然也可以加入自身的信息）。

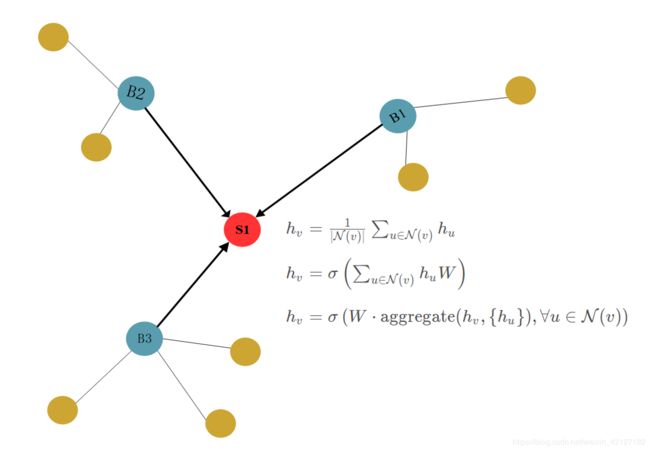
（或者是其他更复杂的手段，但这是之后GCN、GraphSAGE的思路了。）

GGNN的想法就非常简单，对邻居节点求和就是他的信息聚合方式。当邻接矩阵$\mathbf{A}$有边为1，无边为0时，他有个更紧致的表达形式。

$h_v=1\cdot {\sum }_{u\in \mathcal{N}(v)}{h}_u+0\cdot {\sum }_{u\notin \mathcal{N}(v)}{h}_u={\mathbf{A}}_{v:}^{\top }\mathbf{H}$

如果再加上偏置项，我们就得到了论文中描述的公式(2):

${\mathbf{a}}_v^{(t)}={\mathbf{A}}_{v:}^{\top }{\left[{\mathbf{h}}_1^{(t-1)\top }\dots {\mathbf{h}}_{|\mathcal{V}|}^{(t-1)\top }\right]}^{\top }+\mathbf{b}$

GGNN原论文没有提及平均，SRGNN采取了平均的方式，也就是归一化邻接矩阵$\mathbf{A}$。平均并非必须，但我以为平均或者加权平均是有意义的。

一个可能的解释是：每个邻居传递来的信息都包含一个噪音$ϵ$，做了求和后，噪音也会随之增大，平均后可以使得噪音不会因为邻居数增多。

另一个可能的解释来自随机游走的思想，假设不区分邻居节点，一个节点有等分的概率游走到某一个邻居节点。

当然，你会说每个节点传递来的信息重要性不一定一样，或者说边的权重应当不同，应当加权平均，那就是GAT做的工作了。SRGNN也提到了weighted connections，但也只是简单的除以节点的度做平均。

不同类型的边

GGNN认为出边和入边是不同的，需要分别计算。

出边、入边分别构成邻接矩阵，两个邻接矩阵拼接在一起（这是形式上的表示，代码实现时可以分开计算，不一定要拼接在一起）。以SRGNN的图示为例：

不仅仅是出入边的区分，如果图中有多种边，可以同样拼接在后面，我所见到的一个第三方实现³似乎是这样。这有点类似于多层卷积的层次化特征提取思想，每一种边对应不同的权重。

但GGNN提供的概念图没有展示这种不断拼接的做法，只是说参数决定于边的类型和方向。如果不用拼接，简单的情形是为每种边分配一个固定的权重。

每种边代入其embedding应该也是可行的，不过维度变化后需要进行映射。

关于padding的疑惑

GGNN在第一步对$L_V$维的节点特征向量用0填补，扩充至$D$维，这里实在让人困惑，论文只是说通过这样的方式让hidden state的维度大于特征向量annotation。这确实是一种方式，但私以为state维度未必需要大于feature（annotation），也未必需要区分state和feature，state就是和embedding一个向量空间中也未尝不可。即便一定要有一个维度更大的状态向量，加一个矩阵做线性变换映射不也可以吗。

SRGNN是随机初始化的embedding，然后再通过权重矩阵$\mathbf{H}$映射为hidden state。

我实在没有想到一定要填补0的情形，如果读者有其他的领会，还请麻烦解惑。

传播

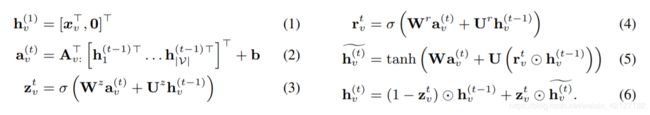
与GRU类比，需要两个输入向量：$a_v^{(t)}$作为当前时间步的输入向量，$h_v^{(t-1)}$为上一时间步的状态向量。接下来和GRU一样得到遗忘门 $\mathbf{z}$ 和重置门 $\mathbf{r}$，最后得到新时刻的状态向量$h_v^{(t)}$，可以直接作为节点的embedding，但也可以和GNN一样再映射一次；
${\mathbf{o}}_n=g_{\mathbf{w}}\left({\mathbf{x}}_n,{\mathbf{l}}_n\right)$
如果是整张图输出一个向量，采取soft attention的形式加权求和输出：

时间步数是一个自由设置的超参，可以重复实验选择指标最大的超参，设置为1只传播一次也没问题（SRGNN的默认参数）。GGNN不像GRU那样循环次数由输入的序列长度决定，但之所以朝着GRU设计，是因为这样可以得到一个序列性的输出。

输出模型

该拓展模型称为GGSNN.

${\mathcal{F}}_{\mathcal{X}}^{(k)},{\mathcal{F}}_o^{(k)}$分别负责更新和输出，可以是两个独立的GGNN，也可以共享GGNN的传播层而由两个不同的输出层输出（虽然减少了训练开销，但要求传播行为不同时效果可能不好）。

SRGNN

Motivation

这篇论文独创性并不多，与其说SRGNN，不如称为GGNN4rec，最大的贡献是首次将GNN应用于会话推荐。

无论是最早的HMM，还是基于RNN的模型，一般都把会话视作马尔科夫链，或者说序列建模。

SRGNN将会话历史视作一张有向图，除了考虑某item与相邻的前item的联系外，还考虑了与其他有交互的item之间的联系（会话图中的节点可能会有多个入点出点，但至少比RNN多考虑了后一个item），也就是考虑了上下文的过渡信息。另外，序列推荐的输出来自最后一个item，SRGNN认为会话（尤其是短时间的会话）中应该更考虑整体的信息。

核心模型

SRGNN利用GGNN进行item embedding的计算。

整个数据集item之间的转移构成了一张非常大的图，但SRGNN只考虑一个会话中出现的item构成的子图，在会话不是很长时，就不会有内存溢出的问题。（上面的图示右侧输出了7个item的score，容易引起误会，应该是4个，而非batch中item总数）

SRGNN也是用了data augmentation的方式，将一条session增广为多条，即$[v_1,v_2],[v_1,v_2,v_3],...,[v_1,v_2,...,v_n]$

另外，直接根据图计算，会出现原始序列顺序混淆的情况，比如

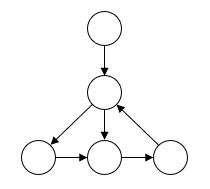
无法明确地指出第二个节点先指向哪个节点，尽管这种情况发生的概率很小。数据增广就可以保证顺序信息的完整。

和GGNN一样，得到的新embedding通过注意力机制计算得到一个global session embedding $s_g$

虽然注意力计算中也单独加入了最近item $v_n$来强调用户的当前兴趣，但SRGNN借鉴NARM，也同时加入了local session embedding，$s_l$可以简单地使用最后一个item的embedding来表示。

然后拼接两个session emb，通过一个Linear层计算出混合的session emb，

最后作为user vector，和item embedding计算score，由交叉熵来控制损失。

同样地，SRGNN也继承了GGNN的缺点，比如复杂的噪声连接和过平滑问题（各节点互相学习削弱了差异）等。

比较

GRU4rec	SRGNN
序列模型，只考虑上一节点到当前节点的过渡关系	图模型，考虑更复杂的过渡关系，包括若干出点和入点与当前节点的联系
仅考虑用户的当前兴趣	使用Attention机制，考虑用户的当前兴趣和整体兴趣
循环次数由序列长度决定	循环次数是个超参，SRGNN默认为1
有负采样，pairwise loss（BPR、TOP1）	没有负采样，pointwise loss（NLL）
minibatch，代码比较复杂	data augmentation，实现比较简单（但序列长度较长时不适用于RNN）

前三行也是GRU和GGNN的区别

---

1. The graph neural network model ↩︎

2. 从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (一) ↩︎

3. ggnn.pytorch ↩︎