更好的理解LSTM - 简单的python实例

1. 为什么用LSTM?
   We use RNN when sequence data is important : https://blog.csdn.net/weixin_43909872/article/details/85567106

RNN的问题：
a. RNN 一般使用tanh作为激活函数，从下面的tanh和tanh导数函数图像可以看到他的梯度和sigmoid一样会下降得非常快，而RNN网络又会循环使用W计算，在BPTT（Back Propagation through time）的时候很容易造成梯度消失

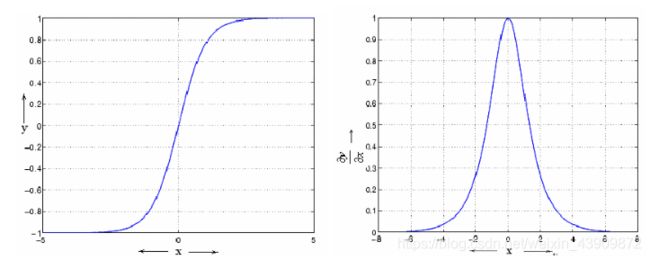
b.当W大于一的时候，因为W要被反复使用，相比于普通神经网络，RNN又更容易发生梯度爆炸的情况
关于gradient Vanishing and Exploding 可以看这篇文章： https://mp.csdn.net/mdeditor/85082198#

由于梯度消失或者爆炸的缺陷，RNN在时序比较长的案例里会表现比较差，比如文本分析的时候如果需要的信息在文章很前面的位置，那么RNN就没法处理——于是LSTM出现了

2. 结合一个简单的例子分析LSTM的原理

关于LSTM的介绍很多，就不赘述了，下面截取两张图作为一个参考
LSTM的网络结构

vanilla RNN和LSTM的隐层激活函数对比

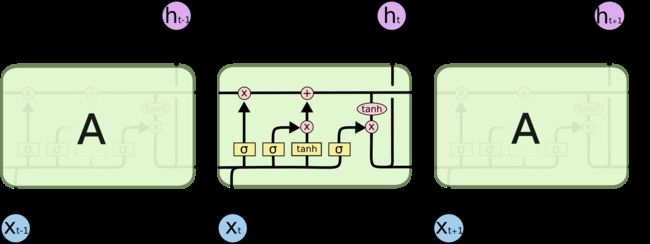
我们的例子：
根据一个4 * 50 的数组，我们要预测一个4 * 1 的数组
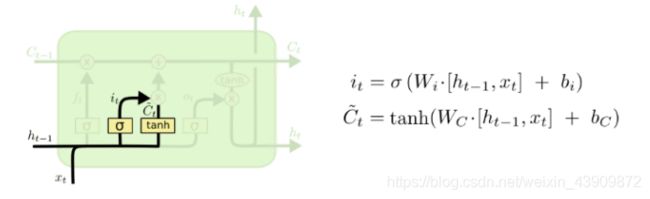
2.1 初始化参数对应上图，看到我们要初始化i,f,o,g的权值和bias，以及他们的偏导数列：

class LstmParam:
    def __init__(self, mem_cell_ct, x_dim):
        self.mem_cell_ct = mem_cell_ct
        self.x_dim = x_dim
        concat_len = x_dim + mem_cell_ct
        # weight matrices
        self.wg = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        self.wi = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len) 
        self.wf = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        self.wo = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        # bias terms
        self.bg = rand_arr(-0.1, 0.1, mem_cell_ct) 
        self.bi = rand_arr(-0.1, 0.1, mem_cell_ct) 
        self.bf = rand_arr(-0.1, 0.1, mem_cell_ct) 
        self.bo = rand_arr(-0.1, 0.1, mem_cell_ct) 
        # diffs (derivative of loss function w.r.t. all parameters)
        self.wg_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.wi_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.wf_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.wo_diff = np.zeros((mem_cell_ct, concat_len)) 
        self.bg_diff = np.zeros(mem_cell_ct) 
        self.bi_diff = np.zeros(mem_cell_ct) 
        self.bf_diff = np.zeros(mem_cell_ct) 
        self.bo_diff = np.zeros(mem_cell_ct) 

2.2 分别看看那些“门”的实现
a. Forget Gate ： 得到上次的状态h(t-1)之后，遗忘门帮我们决定哪些状态需要被移除掉，对应的Wf是遗忘门的权值，Wf的长度需要满足h（t-1） + x（t）

 		# concatenate x(t) and h(t-1)
        xc = np.hstack((x,  h_prev))
        # calculate wf * (h(t-1) & xt) + bf
        self.state.f = sigmoid(np.dot(self.param.wf, xc) + self.param.bf)
        # 
        self.state.s = self.state.g * self.state.i + s_prev * self.state.f

b. Input Gate ： 输入门用来控制当前输入新生成的信息中有多少信息可以加入到细胞状态 Ct 中。tanh 层用来产生当前时刻新的信息，sigmoids 层用来控制有多少新信息可以传递给细胞状态。

       self.state.g = np.tanh(np.dot(self.param.wg, xc) + self.param.bg)
       self.state.i = sigmoid(np.dot(self.param.wi, xc) + self.param.bi)

然后计算现在的细胞状态，这个细胞状态有前面遗忘门的结果和输入门的结果决定：

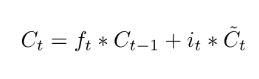
self.state.s = self.state.g * self.state.i + s_prev * self.state.f

c. Output Gate : 最后，基于现在的细胞状态，输出隐藏状态 h（t） 。这里依然用 sigmoid层 (输出门，o（t）) 来控制有多少细胞状态信息 (tanh(Ct)，将细胞状态缩放至 (−1,1) 可以作为隐藏状态的输出 h（t）。

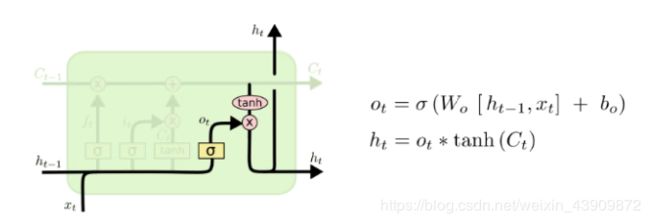
        self.state.o = sigmoid(np.dot(self.param.wo, xc) + self.param.bo)
        self.state.h = self.state.s * self.state.o

3. 总结
   对比下面LSTM的梯度下降图和原来的RNN反向传播图，我们可以发现：
   a. W并没有参与多次乘法计算，而参与更多的是f(x)，计算量显著下降，性能提升
   b. 反向传播过程会遇到不同的f（x），梯度消失或者爆炸的几率降低，在实践中能很好的优化深度时间序列的问题
   

4. 代码和实验结果：
   代码：https://github.com/manik9/LSTMs
   实验结果：

......
iter 93: y_pred = [-0.50039,  0.20148,  0.09880, -0.49899], loss: 4.784e-06
iter 94: y_pred = [-0.50038,  0.20140,  0.09886, -0.49904], loss: 4.323e-06
iter 95: y_pred = [-0.50037,  0.20132,  0.09892, -0.49908], loss: 3.907e-06
iter 96: y_pred = [-0.50036,  0.20125,  0.09897, -0.49912], loss: 3.531e-06
iter 97: y_pred = [-0.50035,  0.20119,  0.09903, -0.49915], loss: 3.193e-06
iter 98: y_pred = [-0.50034,  0.20112,  0.09908, -0.49919], loss: 2.887e-06
iter 99: y_pred = [-0.50033,  0.20106,  0.09912, -0.49923], loss: 2.611e-06